A ship moves with velocity v=36km per hour along an arc of a circle of radius R=200m. Find the moment of the gyroscopic forces exerted on the bearings by the shaft with a flywheel whose moment of inertia relative to the rotation axis equals I=3.8⋅103kg⋅m2 and whose rotation velocity n=300r±. The rotation axis is oriented along the length of the ship.
The revolutions per minute of the flywheel being n, the angular momentum of the flywheel is l×2πn. The rate of precession is vR
Thus N=2πINV/R=5⋅97kN.m.
Topper's Solved these Questions
- PHYSICAL FUNDAMENTALS OF MECHANICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:PHYSICAL FUNDAMENTALS OF MECHANICSExercise:Elastic Deformation Of Asolid Body
Explore 25 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:PHYSICAL FUNDAMENTALS OF MECHANICSExercise:Hydrodynamics
Explore 25 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:PHYSICAL FUNDAMENTALS OF MECHANICSExercise:Universal Gravitation
Explore 34 Videos
- OSCILLATIONS AND WAVESBook:IE IRODOV, LA SENA & SS KROTOVChapter:OSCILLATIONS AND WAVESExercise:Electromagnetic Waves, Radiation
Explore 36 Videos
- THERMODYNAMICS AND MOLECULAR PHYSICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:THERMODYNAMICS AND MOLECULAR PHYSICSExercise:Transport Phenomena
Explore 38 Videos
Similar Questions
Disk 1 rotates about a smooth vertical axis with the angular velocity ω1. Disk 2 rotating with the angular velocity ω2 is kept on disk 1 while rotating in the same direction. Find the change in the rotational kinetic energy of the system given that the moments of inertia of the disks relative to the rotation axis are equal to I1andI2, respectively. The constant surface of the disks are rough.
View SolutionA locomotive is propelled by a turbine whose axle is parallel to the axes of wheels. The turbine's rotation direction coincides with that of wheels. The moment of inertia of the turbine rotor relative to its own axis is equal to I=240kg⋅m2. Find the additional force exerted by the gyroscopic forces on the rails when the locomotive moves along a circle of radius R=250m with velocity v=50km per hour. The gauge is equal to l=1.5m. The angular velocity of the turbine equals n=1500r±.
View Solution
Knowledge Check
A body of moment of inertia about its axis of rotation is 3kgm2 and angular velocity 3 rad/s. The kinetic energy of rotating body is same as that of body of mass 27 kg moving with a speed of
A1.0 m/sB0.5 m/sC1.5 m/sD2.0 m/sA cockroach is moving with velocity v in anticlockwise direction on the rim of a disc of radius R of mass m. The moment of inertia of the disc about the axis is I and it is rotating in clockwise direction with an angular velocity ω. If the cockroach stops, the angular velocity of the disc will be
AIωI+mR2BIω+mvRI+mR2CIω−mvRI+mR2DIω−mvRIA particle moves along a circle of radius R =1m so that its radius vector →r relative to a point on its circumference rotates with the constant angular velocity ω=2rad/s. The linear speed of the particle is
A4m/sB2m/sC1m/sD0.5m/s
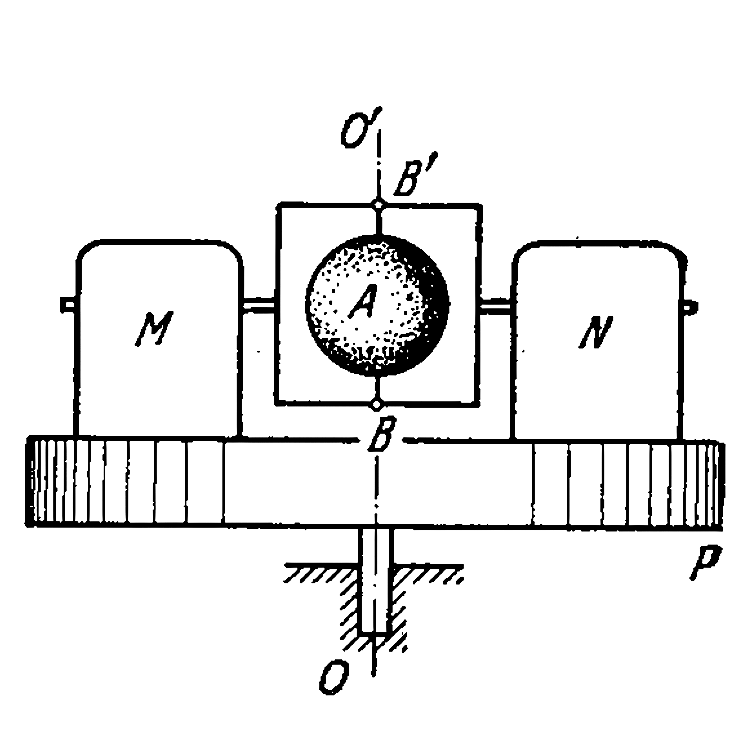
A stationary platform P which can rotate freely about a vertical axis (figure) supports a motor M and a balance weight N. The moment of inertia of the platform with the motor and the balance weight relative to this axis is equal to I. A light frame is fixed to the motor's shaft with a uniform sphere A rotating freely with an angular velocity ω0 about a shaft BB′ coinciding with the axis OO′. The moment of inertia of the sphere relative to the rotation axis is equal to I0. Find
(a) the work performed by the motor in turning the shaft BB′ through 90∘, through 180∘,
(b) the moment of external forces which maintains the axis of the arrangement in the vertical position after the motor turns the shaft BB′ through 90∘.
View SolutionCalculate the angular momentum of a body whose rotational energy is 10 joule. If the angular momentum vector coincides with the axis of rotation and its moment of inertia about this axis is 8×10−7 kg m^(2)
View SolutionA flywheel of moment of inertia 5.0kg−m2 is rotated at a speed of 10rad/s because of the friction at the axis it comes to rest in 10s. Find the average torque of the friction.
View SolutionDemonstrate that in the reference frame rotating with a constant angular velocity ω about a stationary axis a body of mass m experiences the resultant
(a) centrifugal force of inertia Fcf=mω2RC, where RC is the radius vector of the body's centre of inertia relative to the rotation axis,
(b) Coriolis force Fcor=2m[v′Cω], where v′C is the velocity of the body's centre of inertia in the rotating reference frame.
View SolutionA bicycle wheel of radius 0.3 m has a rim of mass 1.0 kg and 50 spokes, each of mass 0.01 kg. What is its moment of inertia about its axis of rotation ?
View Solution

