A small disc and a thin uniform rod of length l, whose mass is η times greater than the mass of the disc, lie on a smooth horizontal plane. The disc is set in motion, in horiozontal direction and perpendicular to the rod, with velocity v, after which it elastically collides with the end of the rod. Find the velocity of the disc and the angular velocity of the rod after the collision. At what value of η will the velocity of the disc after the collision be equal to zero? reverse its direction?
For the closed system (disc+rod), the angular momentum is conserved about any axis. Thus from the conservation of angular momentum of the system about the rotation axis of rod passing through its C.M. gives:
mv12=mv′l2+ηml212ω (1)
(v′ is the final velocity of the disc and ω angular velocity of the rod)
For the closed system linear momentum is also conserved. Hence
mv=mv′+ηmvc (2)
(where vc is the velocity of C.M. of the rod)
From Eqs (1) and (2) we get
vc=lω3 and v−v′=ηvc
Applying conservation of kinetic energy, as the collision is elastic
12mv2=12mv′2+12ηmv2c+12ηml212ω2 (3)
or v2−v′2=4ηv2c and hence v+v′=4vc
v′=4−η4+ηv and ω=12v(4+η)l
Vectorially, noting that we have taken →'v parallel to →v
→'u=(4−η4+η)→v
So, →'u=0 for η=4 adn →'u⏐⏐↓↑⏐⏐→v for η>4

Topper's Solved these Questions
- PHYSICAL FUNDAMENTALS OF MECHANICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:PHYSICAL FUNDAMENTALS OF MECHANICSExercise:Elastic Deformation Of Asolid Body
Explore 25 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:PHYSICAL FUNDAMENTALS OF MECHANICSExercise:Hydrodynamics
Explore 25 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:PHYSICAL FUNDAMENTALS OF MECHANICSExercise:Universal Gravitation
Explore 34 Videos
- OSCILLATIONS AND WAVESBook:IE IRODOV, LA SENA & SS KROTOVChapter:OSCILLATIONS AND WAVESExercise:Electromagnetic Waves, Radiation
Explore 36 Videos
- THERMODYNAMICS AND MOLECULAR PHYSICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:THERMODYNAMICS AND MOLECULAR PHYSICSExercise:Transport Phenomena
Explore 38 Videos
Similar Questions
A uniform rod of mass M and length a lies on a smooth horizontal plane. A particle of mass m moving at a speed v perpendicular to the length of the rod strikes it at a distance a4 from the centre and stops after the collision. Find a. the velocity of the cente of the rod and b. the angular velocity of the rod abut its centre just after the collision.
View SolutionA body of mass M (figure) with a small disc of mass m placed on it rests on a smooth horizontal plane. The disc is set in motion in the horizontal direction with velocity v. To what height (relative to the initial level) will the disc rise after breaking off the body M? The friction is assumed to be absent.
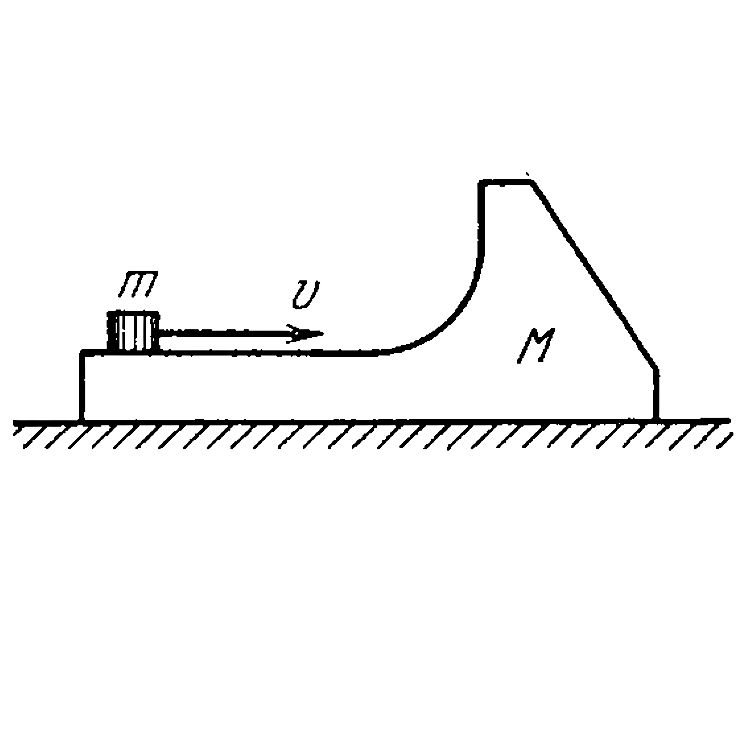
View Solution
Knowledge Check
A uniform rod of length L lies on a smooth horizontal table. The rod has a mass M. A particle of mass m moving with speed v strikes the rod perpendicularly at one of the ends of the rod sticks to it after collision.
Find the velocity of the centre of mass C and the angular, velocity of the system about the centre of mass after the collision.A2mvM+m,3Mv(M+2m)LBMvM+m,6Mv(M+4m)LC2mvM+m,3Mv(M+4m)LDmvM+m,6Mv(M+4m)LA uniform rod of length l and mass 2m rests on a smooth horizontal table. A point of mass m moving horizontally at right angle to the rod with velocity v collides with one end of the rod and sticks to it, then:
Aangular velocity of the system after collision is vlBangular velocity of the system after collision is v2lCthe loss in kinetic enerlgy of the system as a whole as a result of the collision is mv26Dthe loss in kinetic energy of the system as a whole as a result of the collision is 7mv224A uniform rod of length l and mass 2 m rests on a smooth horizontal table. A point mass m moving horizontally at right angles to the rod with velocity v collides with one end of the rod and sticks it. Then
Aangular velocity of the system after collision is 25vlBangular velocity of the system after collision is v2lCThe loss in kinetic energy of the system as a whole as a result of the collision 310mv2DThe loss in kinetic energy of the system as a whole as a result of the collision 7mv224
Three identical discs A, B, and C (figure) rest on a smooth horizontal plane. The disc A is set in motion with vector v after which it experiences an elastic collision simultaneously with the discs B and C. The distance between the centres of the latter discs prior of the collision is η times greater than the diameter of each disc.
Find the velocity of the disc A after the collision. At what value of η will the disc A recoil after the collision, stop, move on?

View SolutionA uniform rod of mass M and length l is placed on a smooth- horizontal surface with its one end pivoted to the surface. A small ball of mass m moving along the surface with a velocity v0, perpendicular to the rod, collides elastically with the free end of the rod. Find:
a. the angular velocity of the rod after collision.
b. the impulse applied by the pivot on the rod during collision. (Take M/m=2)
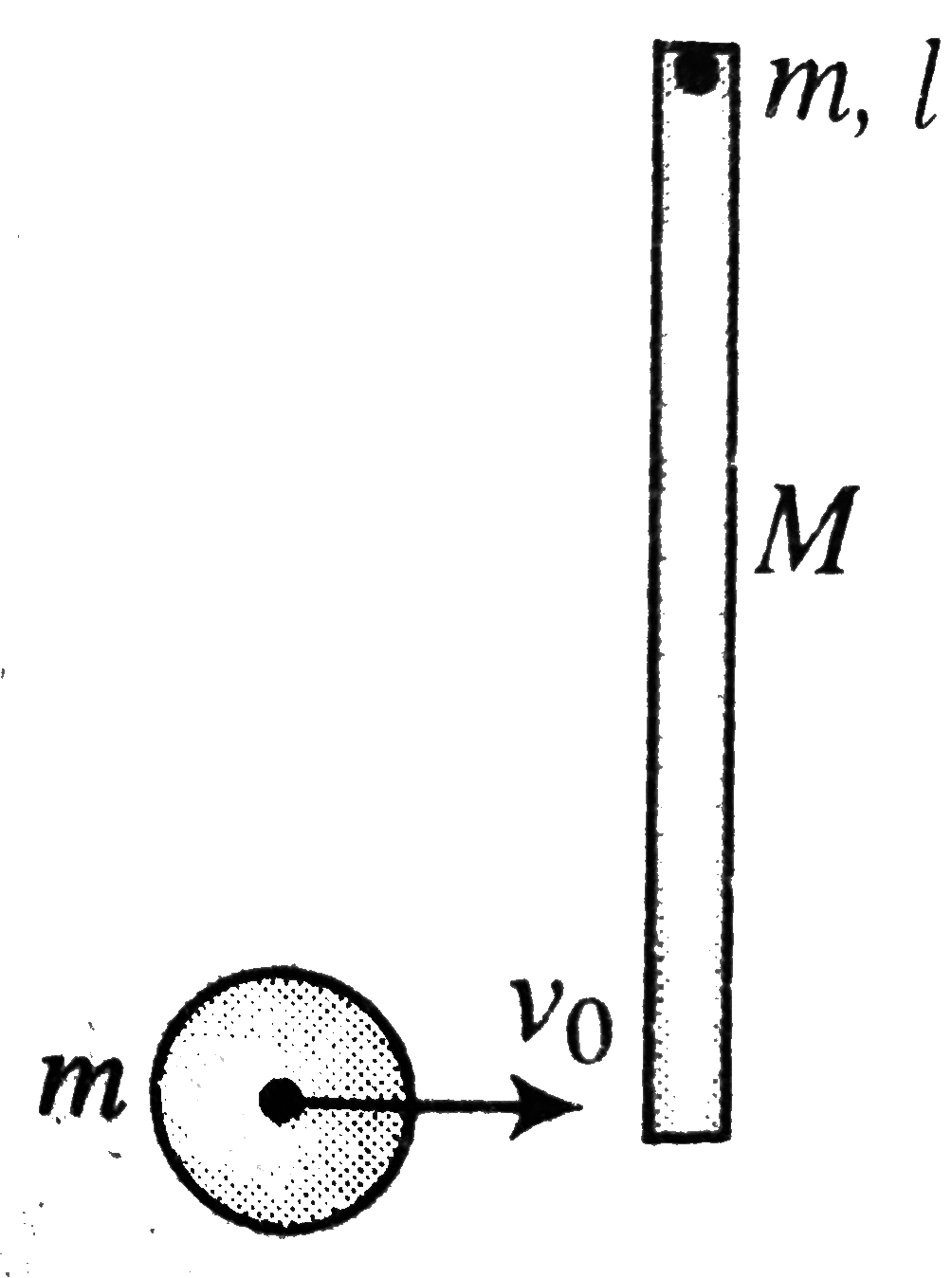
View SolutionA uniform rod of mass M and length L lies on a smooth horizontal plane. A particle of mass m moving at a speed v perpendicular to the length of the rod strikes it at a distance L/6 from the center and stops after the collision. Find
(a) the velocity of center of mass of rod and
(b) the angular velocity of the rod about its center just after collision.
View SolutionA rod od length l is moving in a vertical plane (x−y) when the owest point A of the rod is moved with a velociy v. find the a angular velocity of the rod and b velocity of the end B.

View SolutionA uniform rod of length l and mass 2m rests on a smooth horizontal table. A point mass m moving horizontally at right angles to the rod with initial velocity v collides with one end of the rod and sticks to it.
Determine the position of the point on the rod which remains stationary immediately after collision.
View Solution

