A stationary platform P which can rotate freely about a vertical axis (figure) supports a motor M and a balance weight N. The moment of inertia of the platform with the motor and the balance weight relative to this axis is equal to I. A light frame is fixed to the motor's shaft with a uniform sphere A rotating freely with an angular velocity $ω_{0}$ about a shaft $B B^{'}$ coinciding with the axis $O O^{'}$ . The moment of inertia of the sphere relative to the rotation axis is equal to $I_{0}$ . Find
(a) the work performed by the motor in turning the shaft $B B^{'}$ through $90^{\circ}$ , through $180^{\circ}$ ,
(b) the moment of external forces which maintains the axis of the arrangement in the vertical position after the motor turns the shaft $B B^{'}$ through $90^{\circ}$ .

Video Solution

Text Solution

Verified by Experts

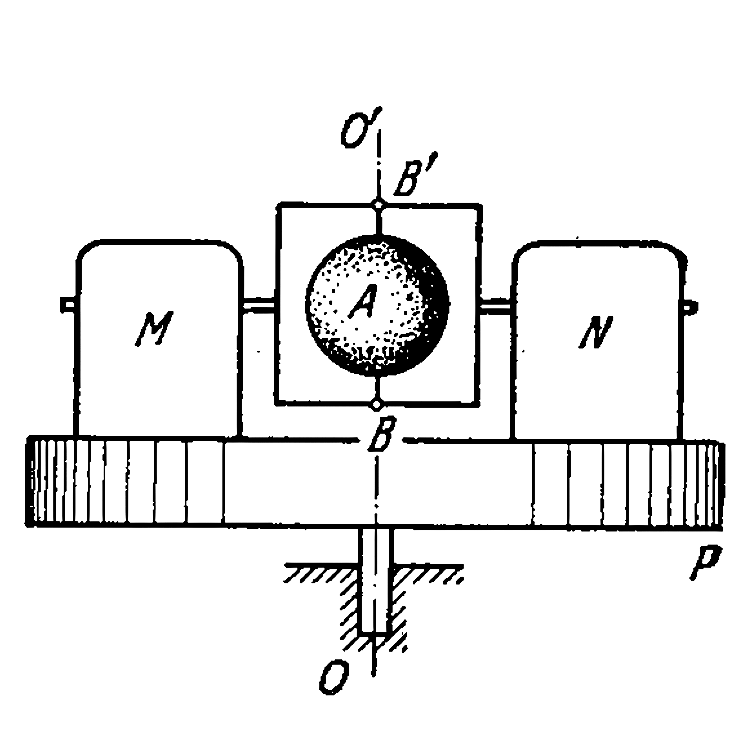
(a) When the shaft $B B^{'}$ is turned through $90^{\circ}$ the platform must start turning with angular velocity $Ω$ so that the angular momentum remains constant. Here
$(I + I_{0}) Ω = I_{0} ω_{0}$ or, $Ω = \frac{I_{0} ω_{0}}{I + I_{0}}$
The work performed by the motor is therefore
$\frac{1}{2} (I + I_{0}) Ω^{2} = \frac{1}{2} \frac{I_{0}^{2} ω_{0}^{2}}{I + I_{0}}$
If the shaft is turned through $180^{\circ}$ , angular velocity of the sphere changes sign. Thus from conservation of angular momentum,
$I Ω - I_{0} ω_{0} = I_{0} ω_{0}$
(Here $- I_{0} ω_{0}$ is the complete angular momentum of the sphere i.e. we assume that the angular velocity of the sphere is just $- ω_{0}$ ). Then
$Ω = 2 I_{0} \frac{ω_{0}}{I}$
and the work done must be,
$\frac{1}{2} I Ω^{2} + \frac{1}{2} I_{0} ω_{0}^{2} - \frac{1}{2} I_{0} ω_{0}^{2} = \frac{2 I_{0}^{2} ω_{0}^{2}}{I}$
(b) In the case (a), first part, the angular momentum vector of the sphere is precessing with angular velocity $Ω$ . Thus a torque,
$I_{0} ω_{0} Ω = \frac{I_{0}^{2} ω_{0}^{2}}{I + I_{0}}$ is needed.

Updated on:21/07/2023

A rod is rotating with angular velocity $ω$ about axis AB. Find $cos θ$ .

A $\frac{g}{2 l ω^{2}}$
B $\frac{g}{l ω^{2}}$
C $\frac{2 g}{{(l ω)}^{2}}$
D $\frac{3 g}{2 l ω^{2}}$
A body is rotating uniformly about a vertical axis fixed in an inertial frame. The resultant force on a particle of the body not on the axis is
Avertical
Bhorizontal and skew with the axis
Chorizontal and intersecting the axis
Dnone of these
A disc of moment of inertia $I_{1}$ is rotating freely with angular speed $ω_{1}$ when another non-rotating disc of moment of inertia $I_{2}$ is dropped on it. The two discs then rotate as one unit. Find the final angular speed.
A $\frac{I_{1} ω_{1}}{I_{2}}$
B $\frac{I_{2} ω_{1}}{I_{2} + I_{2}}$
C $\frac{I_{1} ω_{2}}{I_{1} + I_{2}}$
D $\frac{(I_{1} + I_{2})}{I_{2} ω_{1}}$