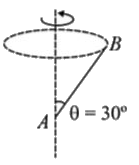
A uniform rod of mass $m$ and length $l_{0}$ is rotating with a constant angular speed $ω$ about a vertical axis passing through its point of suspension. Find the moment of inertia of the rod about the axis of rotation if it make an angle $θ$ to the vertical (axis of rotation).

Video Solution

Text Solution

Verified by Experts

We can observe that each and every element of rod is rotating with different radius about the axis of rotation.
Take an elementary mass $d m$ of the rod.

$d m = \frac{m}{l_{0}} d l$
The moment of inertia of the elementary mass is given as $d l = (d m) r^{2}$
The moment of inertia of the rod
$= I = \int d I \Rightarrow I = \int r^{2} d m$
Substituting $r = l sin θ$ and $d m = m l_{0} . d l$ we obtain
$I = \int (l^{2} {sin}^{2} θ) \frac{m}{l_{0}} d I = \frac{m {sin}^{2} θ}{l_{0}} \int_{0}^{l_{0}} l^{3} d l = \frac{m l_{0}^{3}}{3 l_{0}} {sin}^{2} θ$
$\Rightarrow l = \frac{m l_{0}^{2} {sin}^{2} θ}{3}$

|

Updated on:21/07/2023

Class 11 PHYSICS RIGID BODY DYNAMICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One or More
A thin uniform rod of mass $m$ and length $L$ rotates with the constant angular velocity $ω$ about .the vertical axis passing through the rod's suspensjon point $O$ . It describes a carried surface, then:
Acentrifugal force acting on rod is $m \frac{L}{2} sin θ ω^{2}$ and will pass through centre of mass
Bcentrifugal force acting on rod is $m \frac{L}{2} sin θ ω^{2}$ and will not pass through centre of mass
C $θ = {cos}^{- 1} (\frac{3 g}{2 ω^{2} L})$
D $θ = {cos}^{- 1} (\frac{g}{ω^{2} L})$
Question 2 - Select One
A uniform rod of mass $m$ and length $l$ rotates in a horizontal plane with an angular velocity $ω$ about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is
A $\frac{1}{2} m ω^{2} x$
B $\frac{1}{2} m ω^{2} (1 - \frac{x^{2}}{l})$
C $\frac{1}{2} m ω^{2} l (1 - \frac{x^{2}}{l^{2}})$
D $\frac{1}{2} m ω^{2} l [1 - \frac{x}{l}]$
Question 3 - Select One
A uniform metal rod is rotated in horizontal plane about a vertical axis passing through its end at uniform rate. The tension in the rod is
Asame at all points
Bdifferent at differen points and maximum at centre of rod
Cdifferent at different points and minimum at axis of rotation.
Ddifferent at different points and maximum at axis of rotation

CENGAGE PHYSICS-RIGID BODY DYNAMICS 1-Integer

Home
Ask Doubt
Profile