A light rigid rod of length 4m is connected rigidly with two identical particles each of mass m=2kg. the free end of the rod is smoothly pivoted at O. The rod is released from rest from its horizontal position at t=0. Find the

angular acceleration of the rod at t=0 (in rads−2).
The correct Answer is:3
Torque equation. The internal forces and the reaction forces at O. Then the net torque about O is
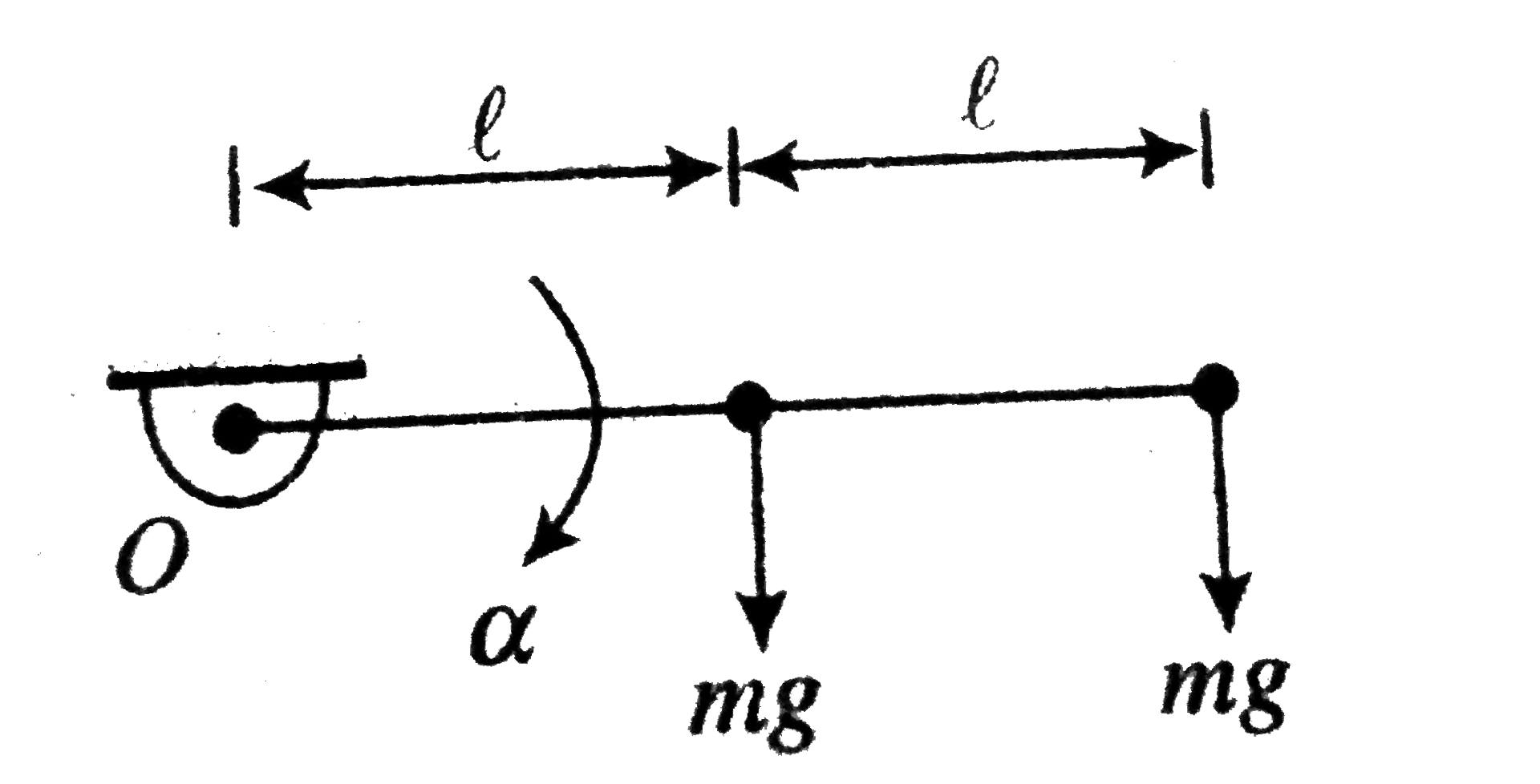 τ0=mgl+mg(2l)=3mgl
τ0=mgl+mg(2l)=3mgl
Which produces an angular acceleraton α. Using Newton's 2nd law of rotation τ=Iα
we have 3mgl=I0α where I0=ml2+m(2I)2=5ml2
This gives α=3g5l=3×105x2=3rads−1
Force equation: Refering FBD. we have (mg+mg)−rR=ma1+ma2

Substitutig a1=Iα and a2=2Iα, we have
R=m(2g−3Iα)
=2(2×10−3×2x3)=2(20−18)=4N
Topper's Solved these Questions
- RIGID BODY DYNAMICS 1Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 1Exercise:Linked Comprehension
Explore 28 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBook:CENGAGE PHYSICSChapter:PROPERTIES OF SOLIDS AND FLUIDSExercise:INTEGER_TYPE
Explore 2 Videos
- RIGID BODY DYNAMICS 2Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 2Exercise:Interger
Explore 2 Videos
Similar Questions
A light rigid rod of length 4m is connected rigidly with two identical particles each of mass m=2kg. the free end of the rod is smoothly pivoted at O. The rod is released from rest from its horizontal position at t=0. Find the
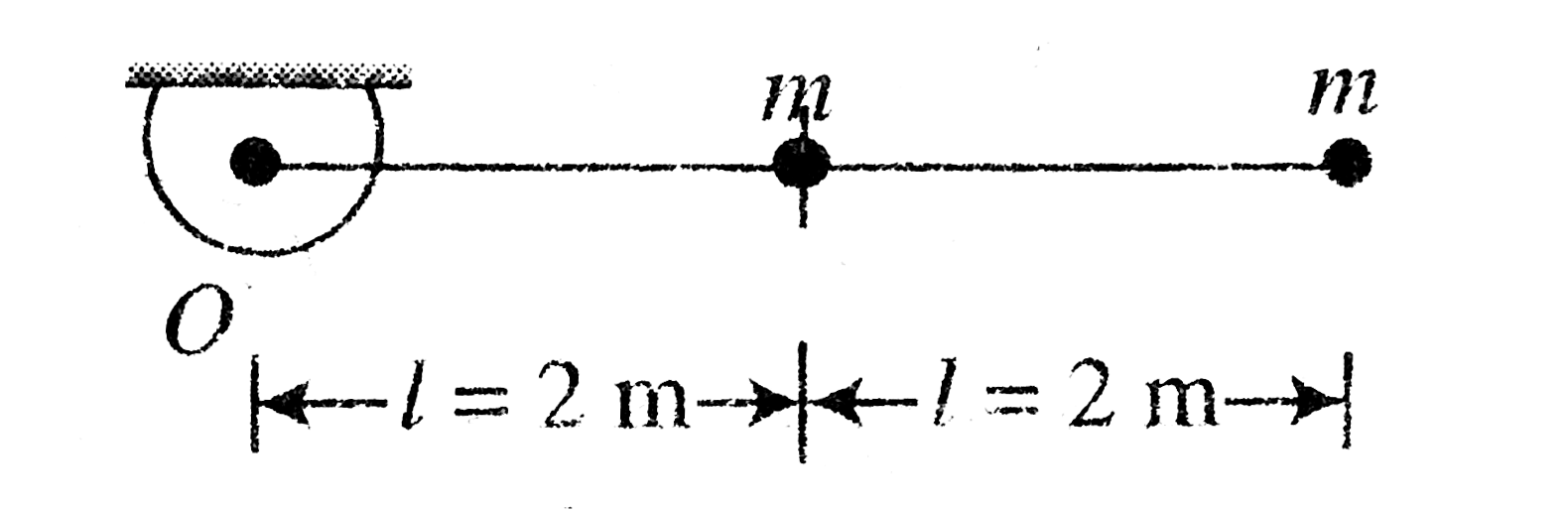
reaction offered by the pivot at t=0 (in N).
View SolutionA uniform rod of length L and mass M is free to rotate about a frictionless pivot at one end. The rod is released from rest in the horizontal position. What are the initial angular acceleration of the rod and the initial linear acceleration of the right end of the Rod ?
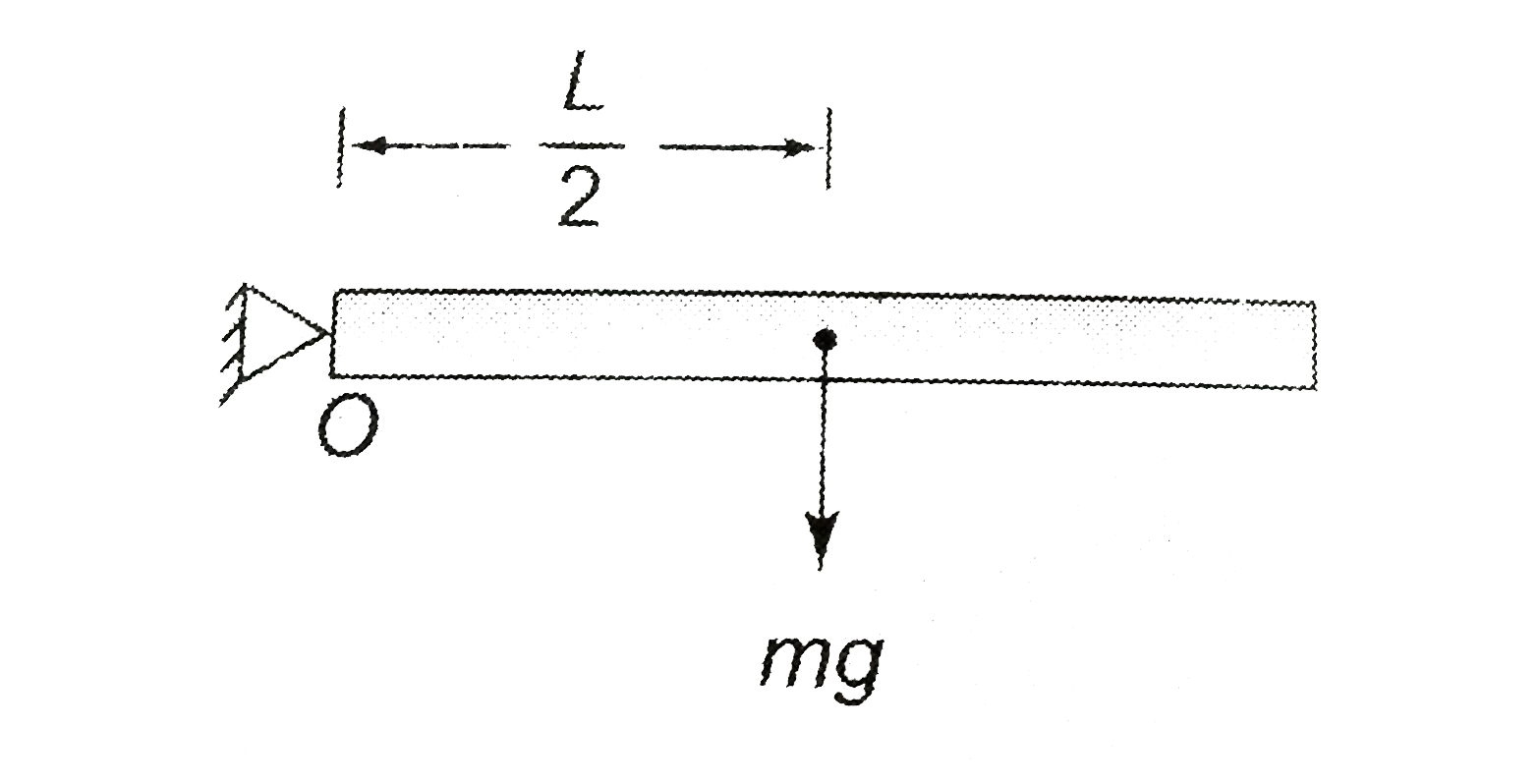
View Solution
Knowledge Check
A uniform rod smoothly pivoted at one of its ends is released from rest. If it swings in vertical plane, the maximum speed of the end P of the rod is.
 .A2√3glB√3glC2√2glD√gl
.A2√3glB√3glC2√2glD√glA uniform rod AB of length l and mass m is free to rotate about point A. The rod is released from rest in the horizontal position. Given that the moment of inertia of the rod about A is ml23, the initial angular acceleration of the rod will be
 A2g3lBmgl2C32glD3g2l
A2g3lBmgl2C32glD3g2lA uniform rod AB of length l and mass m is free to rotate about point A. The rod is released from rest in the horizontal position. Given that the moment of inertia of the rod about A is ml23, the initial angular acceleration of the rod will be
 A2g3lBmgl2C32glD3g2l
A2g3lBmgl2C32glD3g2l
A rigid massless rod of length 3l has two masses attached at each end as shown in the figure. The rod is pivoted at point P on the horizontal axis (see figuare). When released from initial horizontal position, its instantaneous angular acceleration will be

View SolutionA rod of mass m and length l is himged about one of its ends. The rod is released from horizontal position. When the rod becomes vertical, calculate (i) angular speed of the rod (ii) Hinge reaction.
View SolutionA uniform rod of length l and mass M pivoted about its end as shown in Fig. and is free to rotate in the vertical plane about the pivot. The rod is released from rest in the horizontal position.
(a) What is the initial angular acceleration of the rod?

(b) Find the initial acceleration of the right end of the rod?
( c) Find normal contact force due to hinge when rod has rotated through angle θ as shown in Fig.
View SolutionA uniform rod of mass 20 Kg and length 1.6 m is piovted at its end and swings freely in the vertical plane. Angular acceleration of the rod just after the rod is relased from rest in the horizontal position is

View SolutionA uniform rod AB of length l and mass m is free to rotate about point A. The rod is released from rest in the horizontal position. Given that the moment of inertia of the rod about A is ml2/3, the initial angular acceleration of the rod will be
View Solution

