A uniform rod AB of mass 2kg is hinged at one end A. The rod is kept in the horizontal position by a massless string tied to point B. Find the reaction of the hinge (in N) on end A of the rod at the instant when string is cut. (g=10m/s2)

The correct Answer is:5
When the string is cut, the weight of the rod constitutes torque about the hinge, so
τA=mgl2……..i
According to Newton's second law
τA=Iα……….ii
Where α is the angular acceleration of the rod about the end A. From ean i and ii we get
Iα=mgl2
or α=mgl2I
Here I=ml2/3, therefore
∴α=mgl/2ml2/3=32gl
Acceleration of the CM of the rod is
aCM=αr=32gl×l2=3g4
Again by Newtons' second law
mg−RA=maCM
or mg−RA=m×3g4
∴RA=Mg4=2×104=5N
Topper's Solved these Questions
- RIGID BODY DYNAMICS 1Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 1Exercise:Linked Comprehension
Explore 28 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBook:CENGAGE PHYSICSChapter:PROPERTIES OF SOLIDS AND FLUIDSExercise:INTEGER_TYPE
Explore 2 Videos
- RIGID BODY DYNAMICS 2Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 2Exercise:Interger
Explore 2 Videos
Similar Questions
A uniform rod AB of length L and and weight Mg is hinged at one end A. The rod is kept in the horizontal position by a massless string. If the string is cut, then the angular acceleration of the rod will be
[M.I. of the rod about A is ML23]
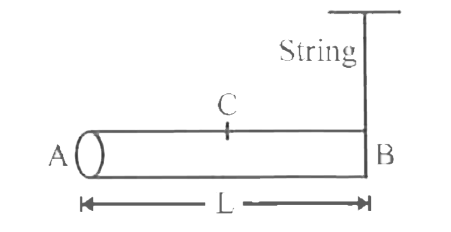
View SolutionA rod PQ of mass M and length L is hinged at end P. The rod is kept horizontal by a masseless string tied to point Q as shown in Fig. When string is cut, the initial angular acceleration of the rod is :

View Solution
Knowledge Check
A rod PQ of mass M and length L is hinged at end P. The rod is kept horizontal by a massless string tied to point Q as shown in figure. When string is cut, the intial angular acceleration of the rod is
 A3g2LBgLC2gLD2g3L
A3g2LBgLC2gLD2g3LA rod PQ of mass M and length L is hinged at end P. The rod is kept horizontal by a massless string tied to point Q as shown in the figure. When string is cut, the initial angular accleration of the rod is.
 A3g2LBgLC2gLD2g3L
A3g2LBgLC2gLD2g3LA uniform rod of mass m, hinged at its upper end, is released from rest from a horizontal position. When it passes through the vertical position, the force on the hinge is
A32mgB2mgC52mgD3mg
A uniform rod of mass M and length L is hinged at its end. The rod is released from its vertical position by slightly pushing it. What is the reaction at the hinge when the rod becomes horizontal, again vertical.
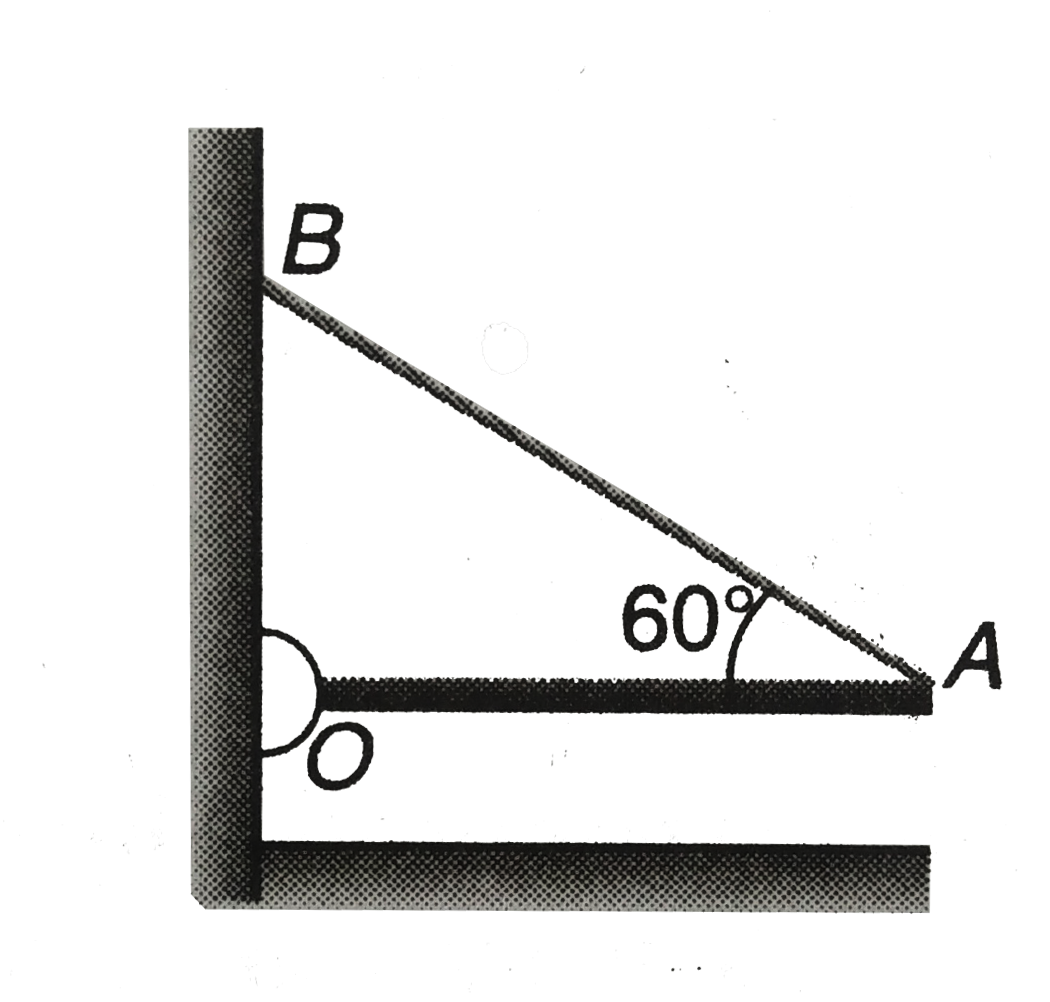
View SolutionA rod OA of mass 4kg is held in horizontal position by a massless string AB as shown in figure. Length of the rod is 2m. Find
(a) tension in the string
(b) net force exerted by hings on the rod. (g=10m/s2)
View SolutionA uniform rod of length 1m and mass 2kg is suspended. Calculate tension T (in N) in the string at the instant when the right string snaps (g=10m/s2).

View SolutionA rod of mass 5 kg is connected to the string at point B. The span of rod is along horizontal. The other end of the rod is hinged at point A. If the string is massless, then the reaction of hinge at the instant when string is cut, is (Take, g=10ms−2)
View SolutionA thin uniform rod mass M and length L is hinged at its upper end. And released from rest from a horizontal position. The tenstion at a point located at a distance L/3 from the hinge point, when the rod become vertical will
View Solution

