A thin uniform rod mass M and length L is hinged at its upper end. And released from rest from a horizontal position. The tenstion at a point located at a distance L/3 from the hinge point, when the rod become vertical will
22Mg/27
11Mg/13
6Mg/11
2Mg

Decrease in gravitational potential energy
= increase in rotatinal kinetic energy
= increase in rotational energy
∴Mg(L)2=12(ML23).ω2∴ω2=3gL
r=L3+2L/32=2L3
T−2Mg3=(2M3)aC=(2M3)(rω2)
∴T=2Mg3+(2Mg3)(2L3)(3gL)
=2Mg
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 2
1 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 2 Subjective
36 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 2 Single Correct
26 Videos
- ROTATIONBOOK - DC PANDEYCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEYCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions
17 Videos
Similar Questions
A uniform rod of mass M and length L is hinged at its end. The rod is released from its vertical position by slightly pushing it. What is the reaction at the hinge when the rod becomes horizontal, again vertical.
View SolutionA uniform slender rod of mass M and length L is pivoted at its end. The rod is released from its nearly vertical position. What is the reaction at the pivot when the rod reaches the horizontal position? If the support is withdrawn at this instant, describe the subsequent motion of the rod.
View Solution
Knowledge Check
A uniform rod of mass m, hinged at its upper end, is released from rest from a horizontal position. When it passes through the vertical position, the force on the hinge is
A32mgB2mgC52mgD3mgOne end of a uniform rod of length l and mass m is hinged at A. It is released from rest from horizontal position AB as shown in figure. The force exerted by the rod on the hinge when it becomes vertical is
 A32mgB52mgC3mgD5mg
A32mgB52mgC3mgD5mgOne end of a uniform rod of length l and mass m is hinged at A. It is released from the rest from horizontal position AB as shown in figure. The force exerted by the rod on the hinge when it becomes verticle is
 A32mgB52mgC3mgD5mg
A32mgB52mgC3mgD5mg
A rod of mass m and length l is himged about one of its ends. The rod is released from horizontal position. When the rod becomes vertical, calculate (i) angular speed of the rod (ii) Hinge reaction.
View SolutionA rod is released from the horizontal position as shown. It is free to rotate about hinge. Find angular velocity of rod when it become vertical?
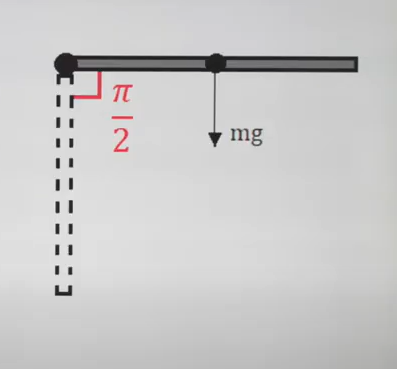
View SolutionA rod of mass m and length l is hinged at 'its' end and released from rest in position shown. Find the force exerted by the hinge when the rod becomes horizontal

View SolutionA metal rod of length l pivoted at is upper end. It is released from a horizontal position. There is a uniform magnetic field ⊥ to its plane of rotation. When it becomes vertical, the p.d. across its ends is proportional to
View SolutionA uniform rod of mass M is hinged at its upper end. A particle of mass m moving horizontally strikes the rod at its mid point elastically. If the particle comes to rest after collision find the value of M/m?

View Solution
