A rod of mass m and length l is himged about one of its ends. The rod is released from horizontal position. When the rod becomes vertical, calculate (i) angular speed of the rod (ii) Hinge reaction.
To solve the problem step by step, we will calculate (i) the angular speed of the rod when it becomes vertical and (ii) the hinge reaction at that moment.
Step 1: Understand the System
We have a uniform rod of mass m and length l hinged at one end. Initially, the rod is horizontal and is released from rest. When the rod becomes vertical, we need to find the angular speed and the hinge reaction.
Step 2: Conservation of Energy
Since the motion is under the influence of gravity, we can use the principle of conservation of mechanical energy. The potential energy lost by the rod as it falls will be converted into kinetic energy.
1. Initial Potential Energy (PE_initial): When the rod is horizontal, the center of mass is at a height l2 (half the length of the rod). Thus,
PEinitial=mgh=mg(l2)=mgl2
The initial kinetic energy (KE_initial) is zero since the rod is at rest.
2. Final Potential Energy (PE_final): When the rod is vertical, the height of the center of mass is 0, so:
PEfinal=0
3. Final Kinetic Energy (KE_final): The kinetic energy when the rod is vertical can be expressed in terms of angular speed ω:
KEfinal=12Iω2
where I is the moment of inertia of the rod about the hinge. For a rod hinged at one end, the moment of inertia is:
I=13ml2
Step 3: Set Up the Energy Conservation Equation
Using the conservation of energy:
PEinitial+KEinitial=PEfinal+KEfinal
Substituting the values:
mgl2+0=0+12(13ml2)ω2
This simplifies to:
mgl2=16ml2ω2
Step 4: Solve for Angular Speed ω
We can cancel m from both sides (assuming m≠0):
gl2=16l2ω2
Multiplying both sides by 6:
3gl=l2ω2
Dividing both sides by l2:
ω2=3gl
Taking the square root:
ω=√3gl
Step 5: Calculate the Hinge Reaction
To find the hinge reaction, we need to consider the forces acting on the rod when it is vertical. The forces acting on the rod are:
- The weight of the rod mg acting downwards at the center of mass (which is at l2).
- The hinge reaction R acting upwards.
Using Newton's second law in the vertical direction:
R−mg=m⋅acm
where acm is the centripetal acceleration of the center of mass. The center of mass moves in a circular path with radius l2, and its centripetal acceleration is given by:
acm=v2r=(l2ω)2l2=l2⋅ω2
Substituting ω2:
acm=l2⋅3gl=3g2
Now substituting back into the force equation:
R−mg=m⋅3g2
Rearranging gives:
R=mg+m⋅3g2=mg+3mg2=5mg2
Final Answers
1. Angular Speed ω:
ω=√3gl
2. Hinge Reaction R:
R=5mg2
We have a uniform rod of mass m and length l hinged at one end. Initially, the rod is horizontal and is released from rest. When the rod becomes vertical, we need to find the angular speed and the hinge reaction.
Since the motion is under the influence of gravity, we can use the principle of conservation of mechanical energy. The potential energy lost by the rod as it falls will be converted into kinetic energy.
PEinitial=mgh=mg(l2)=mgl2
The initial kinetic energy (KE_initial) is zero since the rod is at rest.
PEfinal=0
KEfinal=12Iω2
where I is the moment of inertia of the rod about the hinge. For a rod hinged at one end, the moment of inertia is:
I=13ml2
Using the conservation of energy:
PEinitial+KEinitial=PEfinal+KEfinal
Substituting the values:
mgl2+0=0+12(13ml2)ω2
This simplifies to:
mgl2=16ml2ω2
We can cancel m from both sides (assuming m≠0):
gl2=16l2ω2
Multiplying both sides by 6:
3gl=l2ω2
Dividing both sides by l2:
ω2=3gl
Taking the square root:
ω=√3gl
To find the hinge reaction, we need to consider the forces acting on the rod when it is vertical. The forces acting on the rod are:
- The weight of the rod mg acting downwards at the center of mass (which is at l2).
- The hinge reaction R acting upwards.
R−mg=m⋅acm
where acm is the centripetal acceleration of the center of mass. The center of mass moves in a circular path with radius l2, and its centripetal acceleration is given by:
acm=v2r=(l2ω)2l2=l2⋅ω2
Substituting ω2:
acm=l2⋅3gl=3g2
R−mg=m⋅3g2
Rearranging gives:
R=mg+m⋅3g2=mg+3mg2=5mg2
1. Angular Speed ω:
ω=√3gl
2. Hinge Reaction R:
R=5mg2
Topper's Solved these Questions
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:PRADEEPChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:NCERT
Explore 21 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:PRADEEPChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:ADDITIONAL EXERCISES
Explore 11 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:PRADEEPChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:SOLVED EXAMPLES TYPE E
Explore 1 Video
- RAY OPTICSBook:PRADEEPChapter:RAY OPTICSExercise:Problem For Practice(a)
Explore 25 Videos
- THERMODYNAMICSBook:PRADEEPChapter:THERMODYNAMICSExercise:Assertion- Reason Type Questions
Explore 19 Videos
Similar Questions
A rigid rod of mass m & length l is pivoted at one of its ends. If it is released from its horizontal position, find the speed of the centre of mass of the rod when it becomes vertical.
View SolutionA uniform rod of mass M and length L is hinged at its end. The rod is released from its vertical position by slightly pushing it. What is the reaction at the hinge when the rod becomes horizontal, again vertical.
View Solution
Knowledge Check
A rod of mass m and length l is hinged at 'its' end and released from rest in position shown. Find the force exerted by the hinge when the rod becomes horizontal
 Amg4B3mg2cosθCmg4√9cos2θ+14Dmg2√9cos2θ+14
Amg4B3mg2cosθCmg4√9cos2θ+14Dmg2√9cos2θ+14Two particles each of mass m are attached at end points of a massless rod AB of length l. Rod is hinged at point C as shown. Rod is released from rest from horizontal position. At the instant when rod reaches its vertical position as shown, which of the following is / are correct:
 ASpeed of the particle at B is thrice the speed of particle at ABNet force on particle B is 6mg5CAngular acceleration of the system is zero.DBoth x and y components of hinge force are non-zero
ASpeed of the particle at B is thrice the speed of particle at ABNet force on particle B is 6mg5CAngular acceleration of the system is zero.DBoth x and y components of hinge force are non-zeroA uniform rod of mass m, hinged at its upper end, is released from rest from a horizontal position. When it passes through the vertical position, the force on the hinge is
A32mgB2mgC52mgD3mg
A uniform slender rod of mass M and length L is pivoted at its end. The rod is released from its nearly vertical position. What is the reaction at the pivot when the rod reaches the horizontal position? If the support is withdrawn at this instant, describe the subsequent motion of the rod.
View SolutionA rod is released from the horizontal position as shown. It is free to rotate about hinge. Find angular velocity of rod when it become vertical?
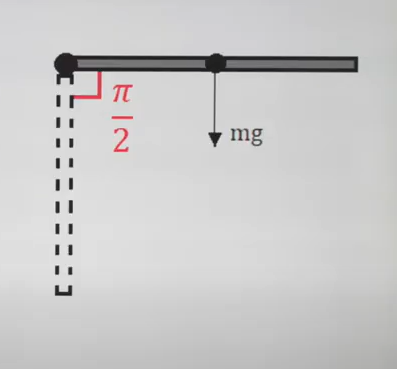
View SolutionA uniform rod of length L and mass M is free to rotate about a frictionless pivot at one end. The rod is released from rest in the horizontal position. What are the initial angular acceleration of the rod and the initial linear acceleration of the right end of the Rod ?
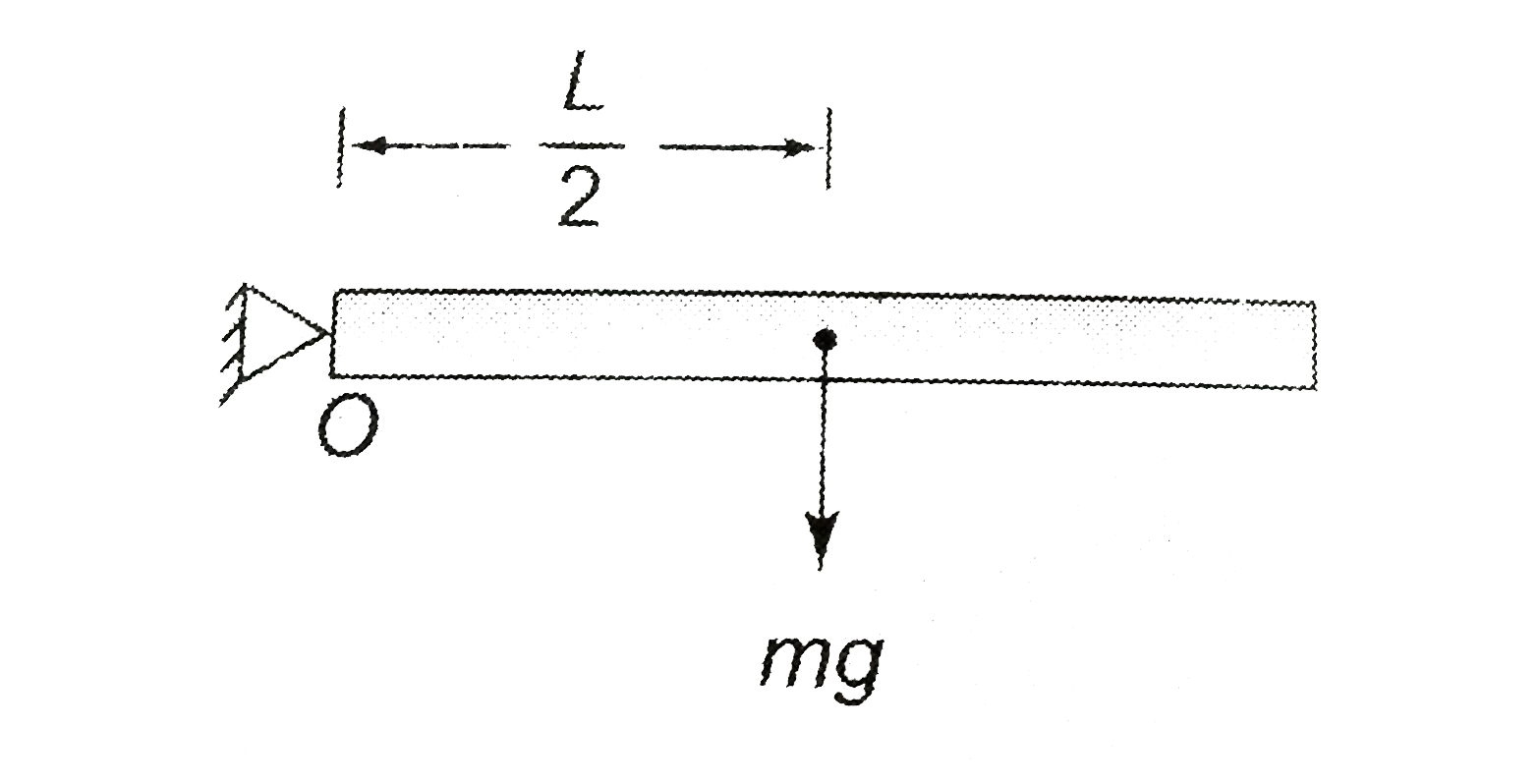
View SolutionA steel rod of length L, density d and cross-sectional area A, is hinged at one end so that it can rotate freely in a vertical plane. The rod is released from a horizontal position. When it becomes vertical, the stress at its midpoint is
View SolutionA steel rod of length L, density d and cross-sectional area A, is hinged at one end so that it can rotate freely in a vertical plane. The rod is released from a horizontal position. When it becomes vertical, the stress at its midpoint is
View Solution

