A string is wrapped around the rim of a wheel of moment of inertia 0.20 kg−m2 nd radius 20 cm. The wheel is free to rotate about it axis. Initially, thewheel is t rest. The string is now pulled by a force of 20 N. Find the angular velocity of the wheel after 5.0 seconds.
Here, I=0.20kgm2
R=20cm=15m
ω1=0,F=20N
ω2=?T=5s
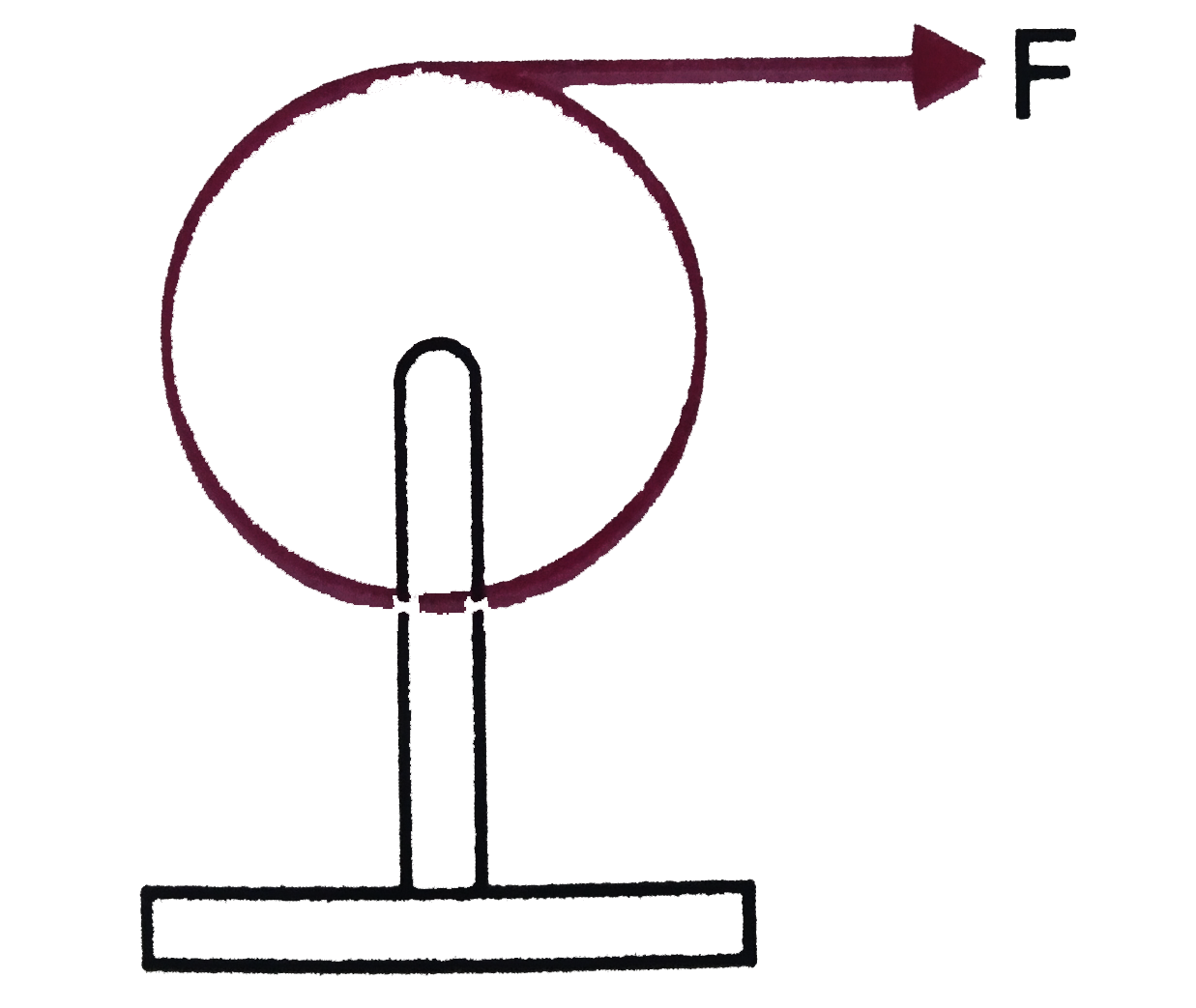
Torque applied on the wheel
τ=F×R=20(1/5)=4N−m
α=τI=40.20=20rad/s2
From ω2=ω1+αt
ω2=0+20×5=100rad/s
Topper's Solved these Questions
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:PRADEEPChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:NCERT
Explore 21 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:PRADEEPChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:ADDITIONAL EXERCISES
Explore 11 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:PRADEEPChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:SOLVED EXAMPLES TYPE E
Explore 1 Video
- RAY OPTICSBook:PRADEEPChapter:RAY OPTICSExercise:Problem For Practice(a)
Explore 25 Videos
- THERMODYNAMICSBook:PRADEEPChapter:THERMODYNAMICSExercise:Assertion- Reason Type Questions
Explore 19 Videos
Similar Questions
A wheel of moment of inertia 0.500kg−m2 and radius 20.0 cm is rotating about its axis at an angular speed of 20.0 rad/s. It picks up a stationary particle of mass 200 g at its edge. Find the new angular speed of the wheel.
View SolutionA string is wrapped on a wheel of moment of inertia 0.20 kg-m^2 and radius 10 cm and goes through a light pulley to support a block of mas 2.0 kg as shown in figure. Find the acceleration of the block.
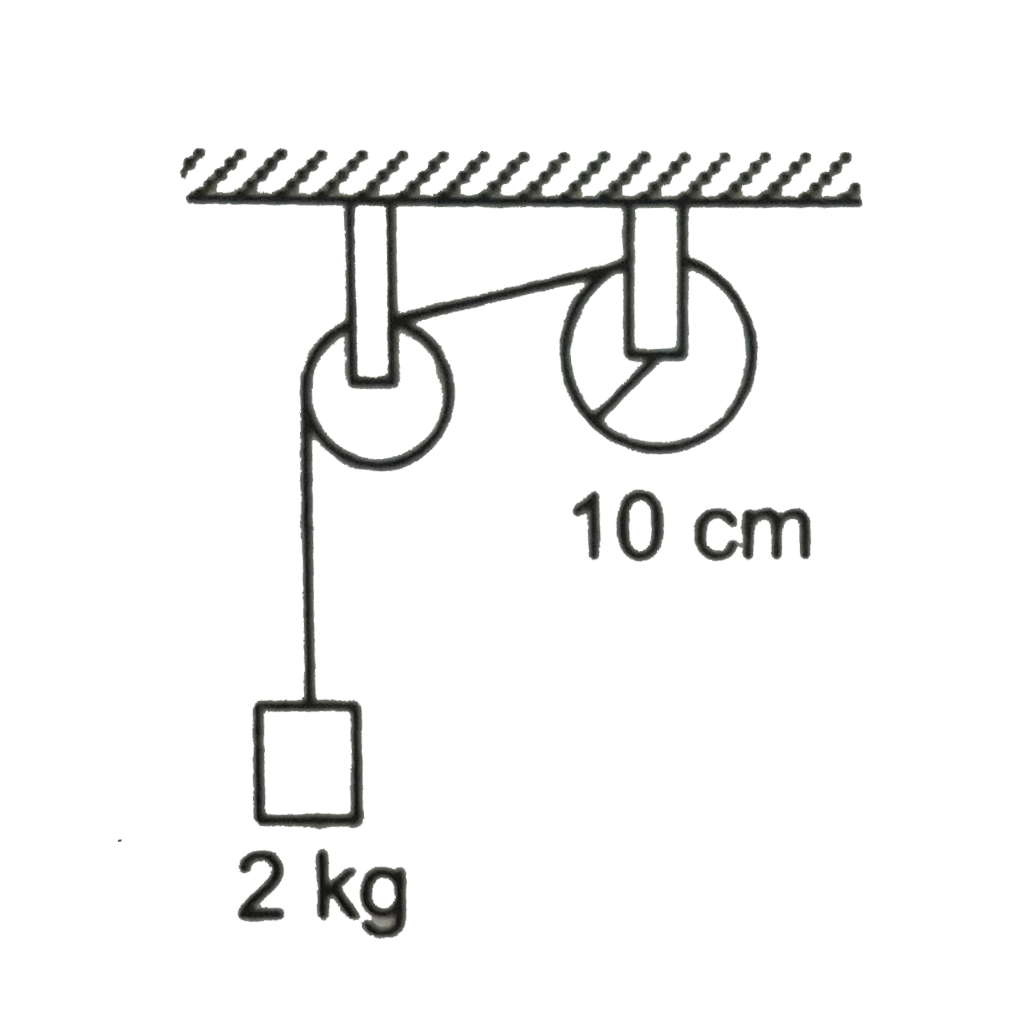
View Solution
Knowledge Check
A flywheel of moment of inertia 0.4 kg m2 and radius 0.2 m is free to rotate about a central axis. If a string is wrapped around it and it is pulled with a force of 10N. Then its angular velocity after 4s will be
A10rads−1B5rads−1C20rads−1DNoneA cord is wound round the circumference of a wheel of radius r. The axis of the wheel is horizontal and its moment of inertia about this axis is I. A weight mg is attached to the end of the cord and is allowed to fall from rest. The angular velocity of the wheel, when the weight has fallen through a distance h, is
A[2ghl+mr]1/2B[2mghI+mr2]1/2C[2mgh1+2mr2]1/2D(2gh)1/2A string is wound round the rim of a mounted flywheel of mass 20 kg and radius 20 cm. A steady pull of 25 N is applied on the cord. Neglecting friction and mass of the string, the angular acceleration of the wheel is
A50 rad s−2B25 rad s−2C12.5 rad s−2D6.25 rad s−2
A pulley has the shape of a uniform solid disc of mass 2kg and radius 0.5m. A string is wrapped over its rim and is pulled by a force of 2.5N. The pulley is free to rotate about its axis. Initially, the pulley is at rest. Find the angular velocity and angle rotated by pulley in 10s.

View SolutionA wheel of mass 2 kg and radius 20 cm initially at rest is free to rotate about its axis. It receives an angular impulse of 4kgm2s−1 initially and similar impulse after every 5 s of initial one. Calculate the angular speed of the wheel 22 s after the initial impulse.
View SolutionA wheel of moment of inertial I and radius R is rotating about its axis at an angular speed ω. It picks up a stationary particle of mass m at its edge. Find the new angular speed of the wheel.
View SolutionA torque of 20N−m is applied on a wheel initially at rest. Calculate the angular momentum of the wheel after 3 sec.
View SolutionA 50 N m torque acts on a wheel with a moment of inertia 150kg⋅m2. If the wheel starts from rest, how long will it take the wheel to make 1 rev?
View Solution

