Two discs of radii Rand2R are pressed against eachother. Initially, disc wit radius R is rotating with angular velocity ω and other disc is stationary. Both discs are hinged at their respective centres and are free to rotate about them. Moment of inertiaof smaller disc is I and of bigger disc is 2I about their respective axis of rotation. Find the angular velocity of bigger disc after long time.
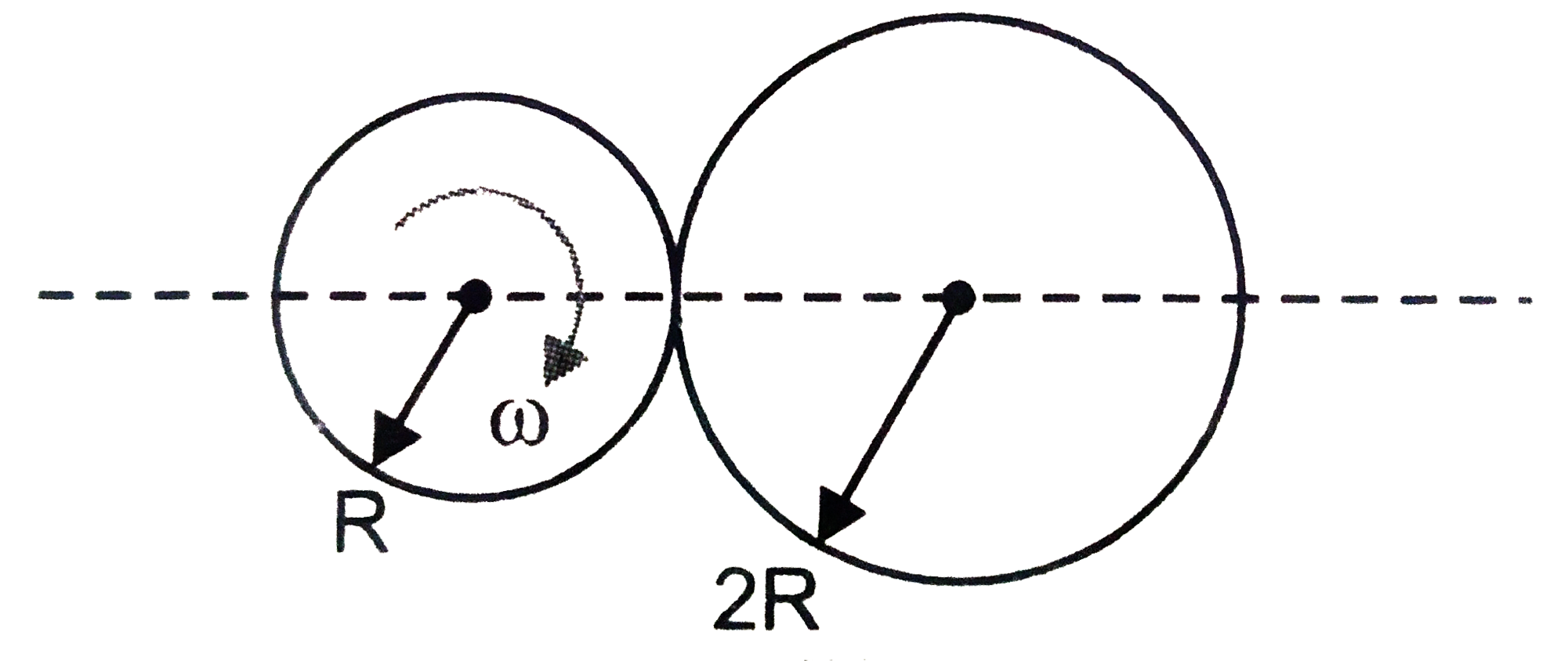
As the discs are pressed against eachother, an equal and opposite frictional force will act on both the discs, till the time rolling starts and hence the linear speed of the circumference of the two discs becomes the same.
Let ω1= angular velocity of smaller disc after long time t
ω2= angular velocity of bigger disc after long time t
f= force of friction between the two discs when rolling starts,
υ1=υ2
ω1R=ω2(2R)∴ω1=2ω2
For smaller disc, τ=f×R=I(ω−ω1)t ..(i)
For bigger disc, τ2=f×2R=2I(ω2−0)t
or f×R=Iω2t ..(ii)
From (i) and (ii), ω−ω1=ω2
or ω−2ω2=ω2
ω=2ω2
or ω=ω/3
Topper's Solved these Questions
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:PRADEEPChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:NCERT
Explore 21 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:PRADEEPChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:ADDITIONAL EXERCISES
Explore 11 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:PRADEEPChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:SOLVED EXAMPLES TYPE E
Explore 1 Video
- RAY OPTICSBook:PRADEEPChapter:RAY OPTICSExercise:Problem For Practice(a)
Explore 25 Videos
- THERMODYNAMICSBook:PRADEEPChapter:THERMODYNAMICSExercise:Assertion- Reason Type Questions
Explore 19 Videos
Similar Questions
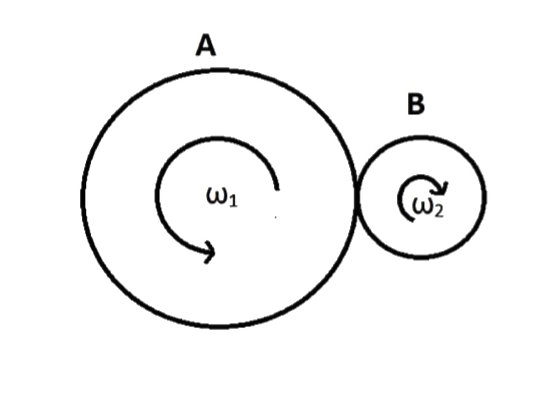
Two discs A and B are in contact and rotating with angular velocity with angular velocities ω1andω2 respectively as shown. If there is no slipping between the discs, then
View SolutionA circular disc of radius R is rotating about its axis O with a uniform angular velocity ωrad s−1 as shown in the figure. The magnitude of the relative velocity of point A relative to point B on the disc is

View Solution
Knowledge Check
A disc of mass m has a charge Q distributed on its surface. It is rotating about an XX' with a angular velocity ω. The force acting on the disc is
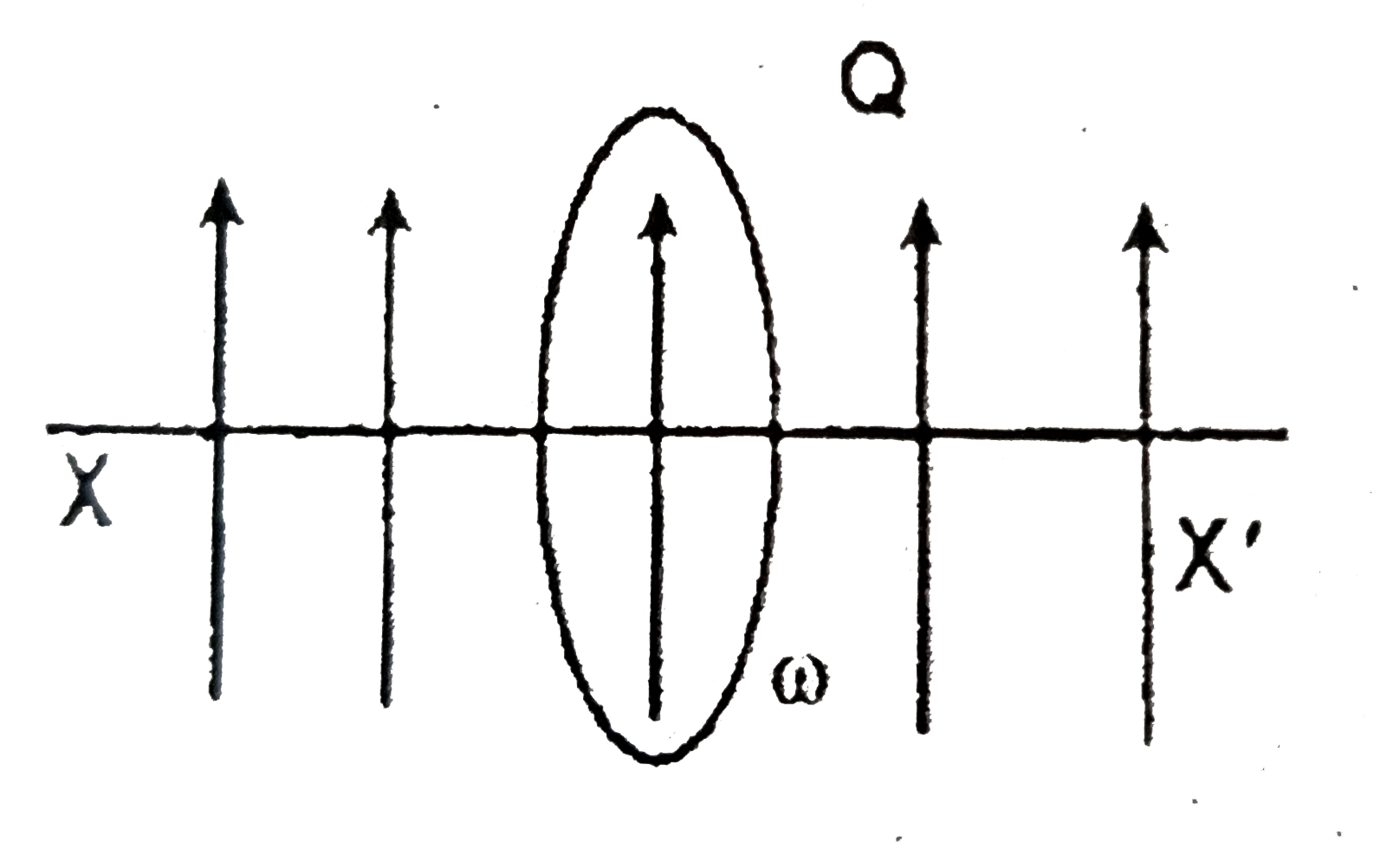 AzeroBωRB/πC2QωBRDnone of these
AzeroBωRB/πC2QωBRDnone of theseA circular disc is rotating about its own axis at uniform rate completes 30 rotations in one minute.The angular velocity of disc in rad s−1 is
A2πBπCπ2Dπ4iA heavy disc is rotating with uniform angular velocity ω about its own axis. A piece of wax sticks to it. The angular velocity of the disc will
AincreaseBdecreaseCbecomes zeroDremain unchanged
A circular disc of mass M and radius R is rotating with angular velocity ω . If two small spheres each of mass m are gently attached to two diametrically opposite points on the edge of the disc, then the new angular velocity of the disc will be
View SolutionA disc of radius R rotates with constant angular velocity ω about its own axis. Surface charge density of this disc varies as σ=αr2, where r is the distance from the centre of disc. Determine the magnetic field intensity at the centre of disc.
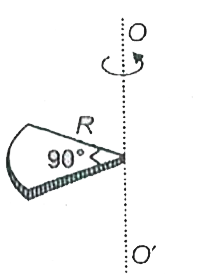
View SolutionA quarter disc of radius R and mass m is rotating about the axis OO' (perpendicular to the plane of the disc) as shown. Rotational kinetic energy of the quarter disc is
View SolutionA constant power is suppied to a rotating disc. The relationship between the angular velocity (ω) of the disc and number of rotations (n) made by the disc is governed by
View SolutionA thin disc of radius R has charge Q distributed uniformly on its surface. The disc is rotated about one of its diametric axis with angular velocity ω. The magnetic moment of the arrangement is
View Solution

