A circular disc of mass M and radius R is rotating with angular velocity ω . If two small spheres each of mass m are gently attached to two diametrically opposite points on the edge of the disc, then the new angular velocity of the disc will be
(M+4mM)ω
(MM+4m)ω
(M+mM)ω
(MM+2m)ω
The correct Answer is:B
I1ω1=I2ω2
∴ 12MR2ω=(12MR2+2mR2)ω'
∴Mω=(M+4m)ω'
∴ω'=(MM+4m)ω
Topper's Solved these Questions
Similar Questions
A thin circular right of mass M and radius R is rotating about its axis with an angular speed ω0 two particles each of mass m are now attached at diametrically opposite points. Find new angular speed of the ring.
View SolutionA disc of mass M and radius r is rotating with an angular velocity ω. If gently, two masses m each are placed at a distance r/2 on either side of the axis of rotation, what will be the new angular velocity ?
View Solution
Knowledge Check
Initial angular velocity of a circular disc of mass M is ω1. Then two small spheres of mass m are attached gently to two diametrically opposite points on the edge of the disc. What is the final angular velocity of the disc -
A(M+mM)ω1B(M+mm)ω1C(MM+4m)ω1D(MM+2m)ω1Initial angular velocity of a circualr disc of mass M is ω1. The tow sphere of mass ma re attached gently to diametrically opposite points ont eh edge of the disc. What is the final angular velocity on the disc?
A(M+mM)ω1B(M+mM)ω1C(MM+4m)ω1D(MM+2m)ω1A thin circular ring of mass M and radius R is rotating about its axis with a constant angular velocity omega. Four objects each of mass m, are kept gently to the opposite ends of two perpendicular diameters of the ring. The angular velocity of the ring will be
AMωM+4mB(M+4m)ωMC(M−4m)ωM+4mDMω4m
A thin circular ring of mass M and radius R is rotating about its axis with a constant angular velocity omega. Four objects each of mass m, are kept gently to the opposite ends of two perpendicular diameters of the ring. The angular velocity of the ring will be
View SolutionA disc of mass M and radius R is rotating about its axis with initial angular velocity of ω0 as shown. Now two small masses of m each one kept on the circumference diametrically opposite to eachother. Find new angular velocity
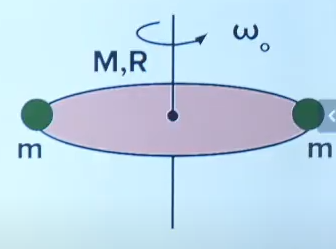
View SolutionA thin circular ring of mass M and radius r is rotating about its axis with constant angular velocity ω . Two objects each of mass m are attached gently to the opposite ends of a diameter of the ring . The ring now rotates with angular velocity given by
View SolutionA thin circular ring of mass Mand radius r is rotating about its axis with a constant angular velocity ω. Four objects each of mass m, are kept gently to the opposite ends of two perpendicular diameters of the ring. The angular velocity of the ring will be
View SolutionA thin circular ring of mass M and radius r is rotating about its axis with a constant angular velocity ω, Two objects, each of mass m, are attached gently to the opposite ends of a diameter of the ring. The wheel now rotates with an angular velocity ω=
View Solution

