A steel rod of length L, density d and cross-sectional area A, is hinged at one end so that it can rotate freely in a vertical plane. The rod is released from a horizontal position. When it becomes vertical, the stress at its midpoint is
13dLg/8
12dLg /8
2dL g/5
dLg/2
The correct Answer is:1
mg12=12×ml23ω2
ω=√3gL
T−m2g=m2ω2×3L4
T=mg2+38×3mg=13mg8
Topper's Solved these Questions
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (A)
32 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (B)
3 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART- C
4 Videos
- SEMICONDUCTORSBOOK - BANSALCHAPTER - SEMICONDUCTORSEXERCISE - CBSE Question
32 Videos
Similar Questions
A uniform rod of length 75cm is hinged at one of its ends and is free to rotate in vertical plane. It is released from rest when rod is horizontal. When the rod becomes vertical, it is breaks at mid− point and lower part now moves freely. The distance of centre of lower part from hinge, when it again becomes vertical for the first time is r. Find the approximate value of 2r.
View SolutionA light rigid rod has a small ball of mass m attached to its one end. The other end is hinged on a table and the rod can rotate freely in vertical plane. The rod is released from vertical position and while falling the ball at its end strikes a hemisphere of mass m lying freely on the table. The collision between the ball and the hemisphere is elastic. The radius of hemisphere and length of the rod are R and 2R respectively. Find the velocity of the hemisphere after collision.
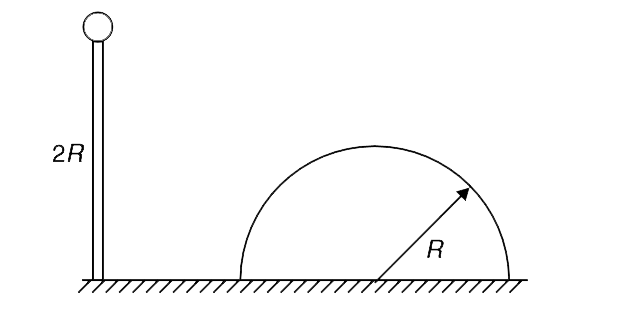
View Solution
Knowledge Check
A uniform rod of mass m and length l is fixed from Point A, which is at a distance l/4 from one end as shown in the figure. The rod is free to rotate in a vertical plane. The rod is released from the horizontal position.

What is the reaction at the hinge, when kinetic energy of the rod is maximum?A47B57mgC137mgD117mgA uniform rod of mass m, hinged at its upper end, is released from rest from a horizontal position. When it passes through the vertical position, the force on the hinge is
A32mgB2mgC52mgD3mgA uniform steel rod of cross- sectional area A and L is suspended so that it hangs vertically. The stress at the middle point of the rod is
A12ρgLB14ρgLCρgLDNone of these
In the figure given in the text if mass of the rod is m then find hinge force.
(a). Just after the rod is released from the horizontal position.
(b). When rod becomes vertical
View SolutionA rod of mass m and length l is himged about one of its ends. The rod is released from horizontal position. When the rod becomes vertical, calculate (i) angular speed of the rod (ii) Hinge reaction.
View SolutionA weightless rigid rod with a load at the end is hinged at point A to the wall so that it can rotate in all directions (Fig).
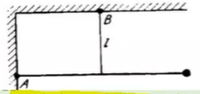
The rod is kept in the horizontal position by a vertical inextensible thread of length 1, fixed at its midpoint. The load receives a momentum in the direction perpendicular to the plane of the figure.
Determine the period T of small oscillations of the system.
View SolutionA uniform rod AB hinged about a fixed point P is initially vertical. A rod is released from vertical position. When rod is in horizontal position:
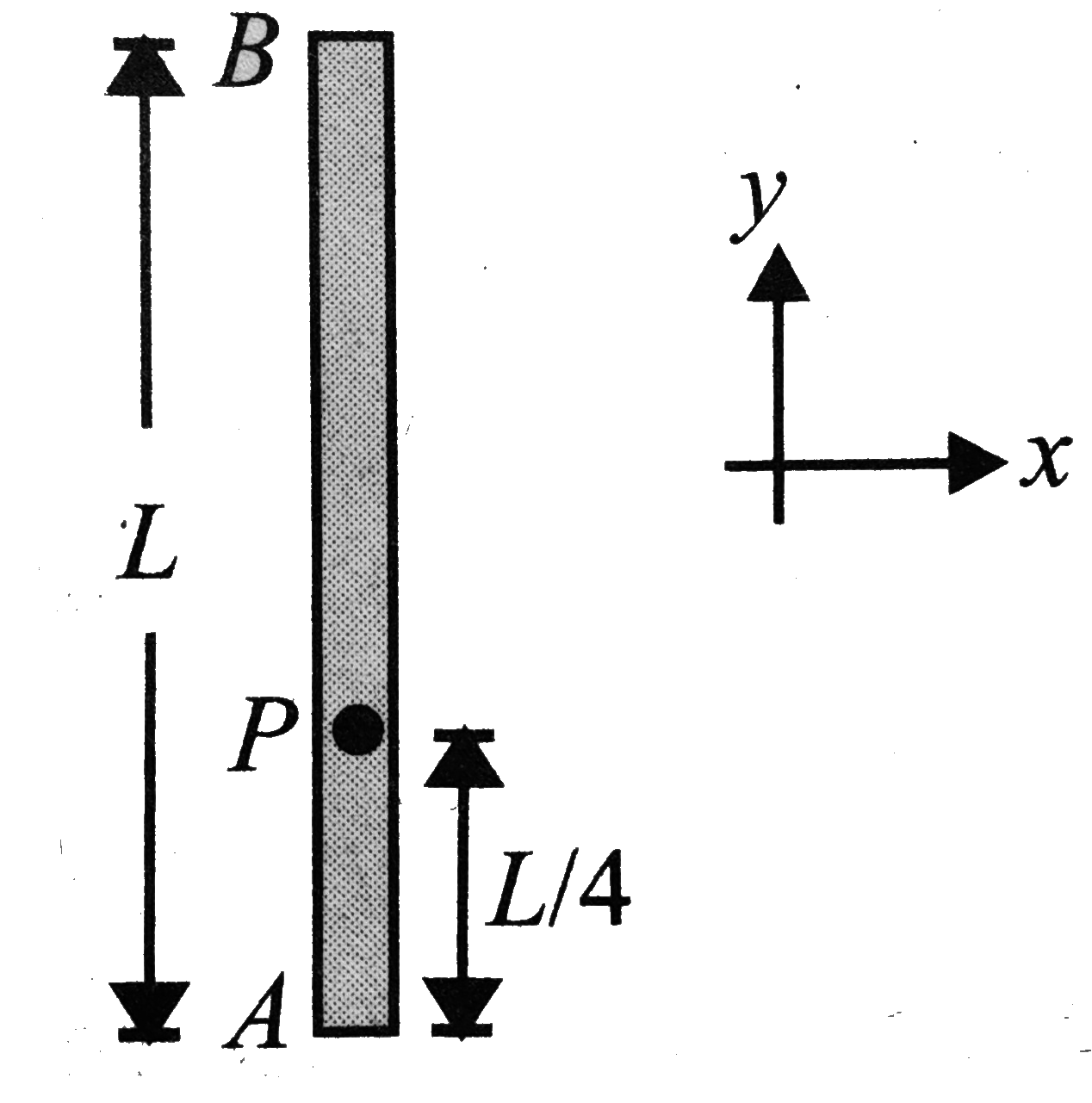
The reaction at hinge P is
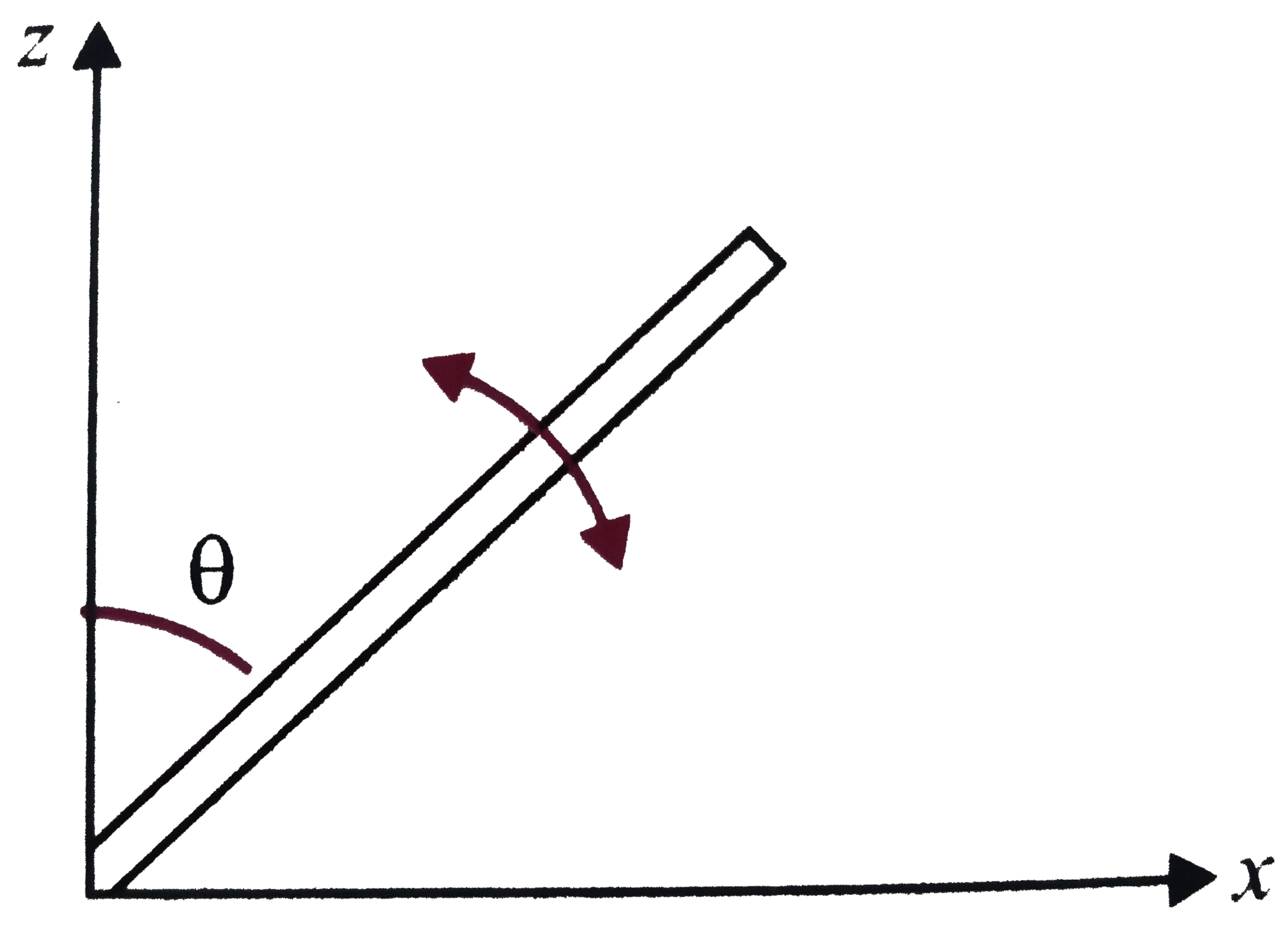
View SolutionA slender uniform rod of mass M and length l is pivoted at one ens so that it can rotate in a vertical plane, Fig. There is negligible friction at the pivot. The free end is held vertically above the pivot and then released. The angular acceleration of the rod when it makes an angle θ with the vertical is
View Solution
