The rod of length l=1m rotates with an angular velocity ω=2rads−1 an the point P moves with velocity v=1ms−1 and acceleration a=1ms−2. Find the velocity and acceleration of Q.
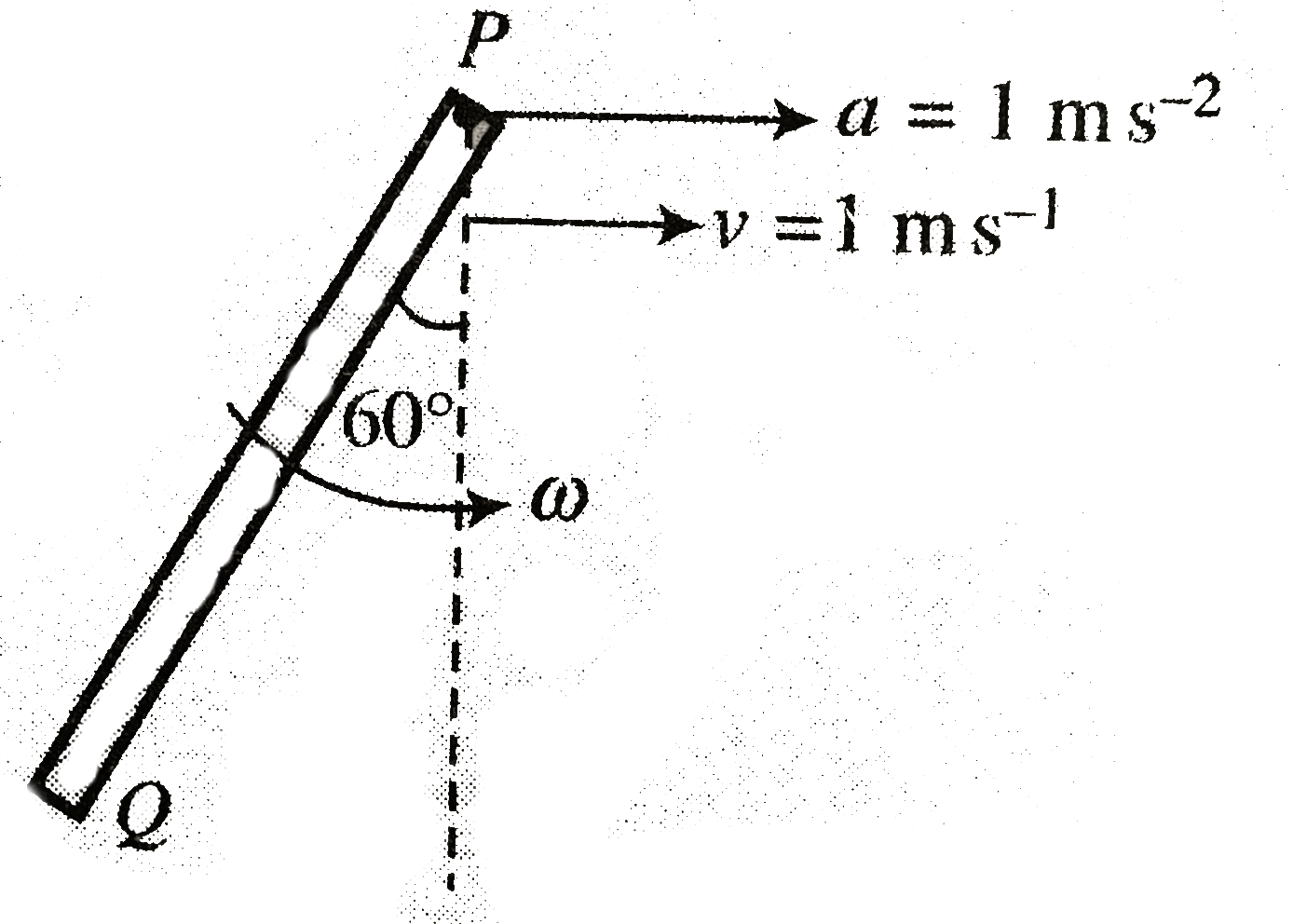
vQ=∣∣→vQP+→vP∣∣=√l2ω2+v2+2vlω120∘

=√(1×2)2+12+2.2(1)(2)×(12)=1ms−1
aQ=∣∣→aQP+→aP∣∣=√a2_(QP)+a2_(P)+2aQPaPcos30∘
where aQP=lω2=2(2)2=4ms−2 and aP=1
√42+12+2.4×1×√32=√17+4√3ms−2
Topper's Solved these Questions
- RIGID BODY DYNAMICS 1Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 1Exercise:Exercise 2.2
Explore 17 Videos
- RIGID BODY DYNAMICS 1Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 1Exercise:Exercise 2.3
Explore 15 Videos
- RIGID BODY DYNAMICS 1Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 1Exercise:Solved Examples
Explore 9 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBook:CENGAGE PHYSICSChapter:PROPERTIES OF SOLIDS AND FLUIDSExercise:INTEGER_TYPE
Explore 2 Videos
- RIGID BODY DYNAMICS 2Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 2Exercise:Interger
Explore 2 Videos
Similar Questions
A particle is moving with initial velocity 1m/s and acceleration a=(4t+3)ms2. Find velocity of particle at t=2sec.
View SolutionA uniform rod of length l is spinning with an angular velocity ω=2vl while its centre of mass moves with a velocity v. Find the velocity of the end of the rod.
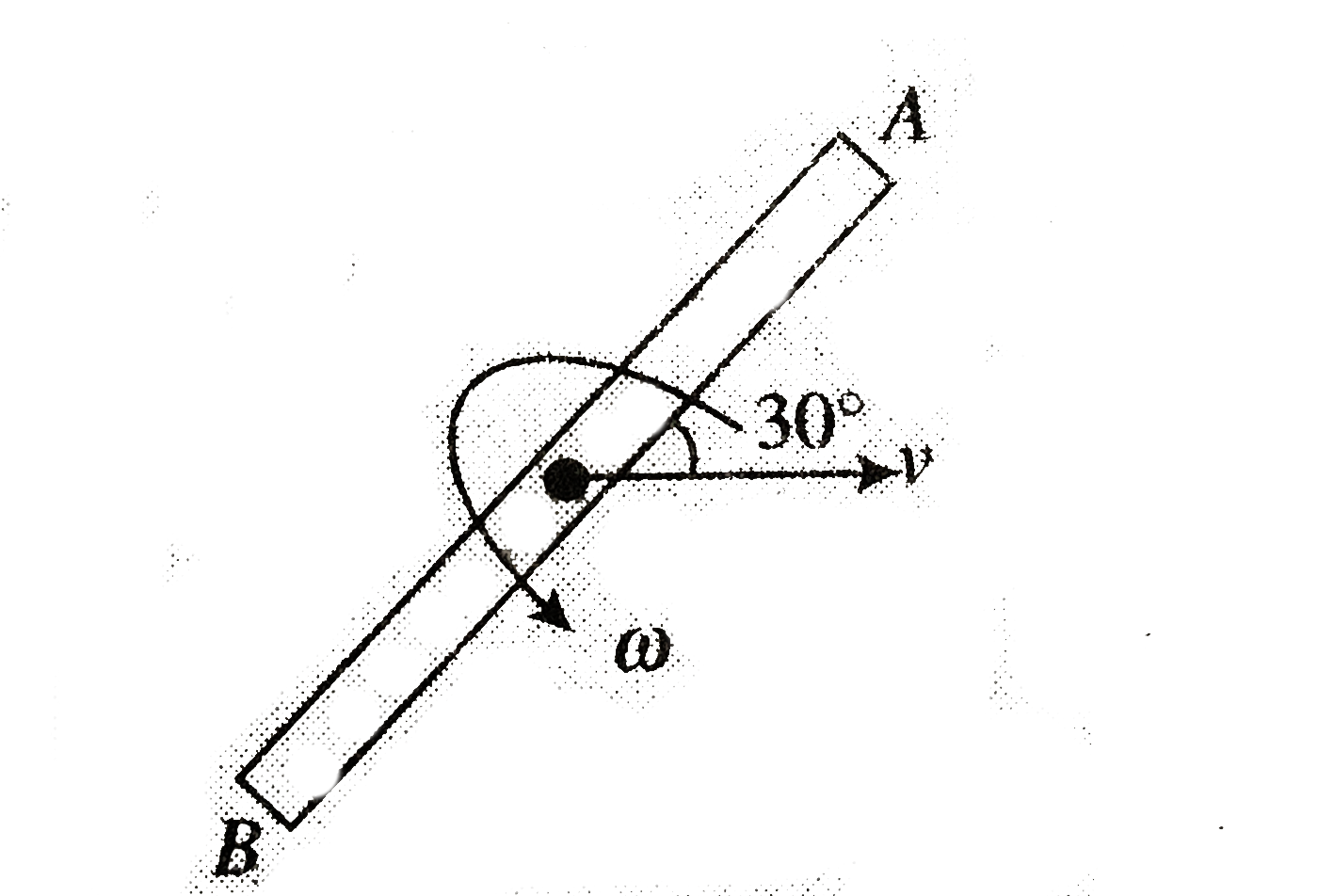
View Solution
Knowledge Check

A rod of length 1 m rotates in the xy plane about the fixed point O in the anticlockwise sense, as shown in figure with velocity ω=a+bt where a=10rads−1 and b=5rads−2. The velocity and acceleration of the point A at t=0 isA+10ˆims−1 and +5ˆims−2B+10ˆjms−1 and (−100ˆi+5ˆj)ms−2C−10ˆjms−1 and (100ˆi+5ˆj)ms−2D−10ˆjms−1 and −5ˆjms−1A uniform rod AB of length l rotating with an angular velocity ω while its centre moves with a linear velocity v=ωl6 If the end A of the rod is suddenly fixed, the angular velocity of
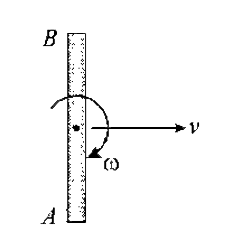 A34ωBω3Cω2D23ω
A34ωBω3Cω2D23ωA body executing SHM has a maximum velocity of 1ms−1 and a maximum acceleration of 4ms−1. Its time period of oscillation is
A3.14sB1.57sC6.28sD0.25s
A wheel is rotating with an angular velocity of 3rads−1. If the angular acceleration is 2rads−1 then calculate its angular velocity after 5 second.
View SolutionThe velocity of a particle is given by v=(2t2−3t+10)ms−1. Find the instantaneous acceleration at t = 5 s.
View SolutionA man A moves due to East with velocity 6ms−1 and another man B moves in N−30∘E with 6ms−1 . Find the velocity of B w.r.t. A.
View SolutionIn a reference frame a man A is moving with velocity (3ˆi−4ˆj)ms−1 and another man B is moving with velocity (ˆi+ˆj)ms−1 relative to A. Find the actual velocity of B.
View SolutionShown in the figure is rod which moves with v=2ms−1 and rotates with ω=2πrads−1. Find the instantaneous axis of rotation.
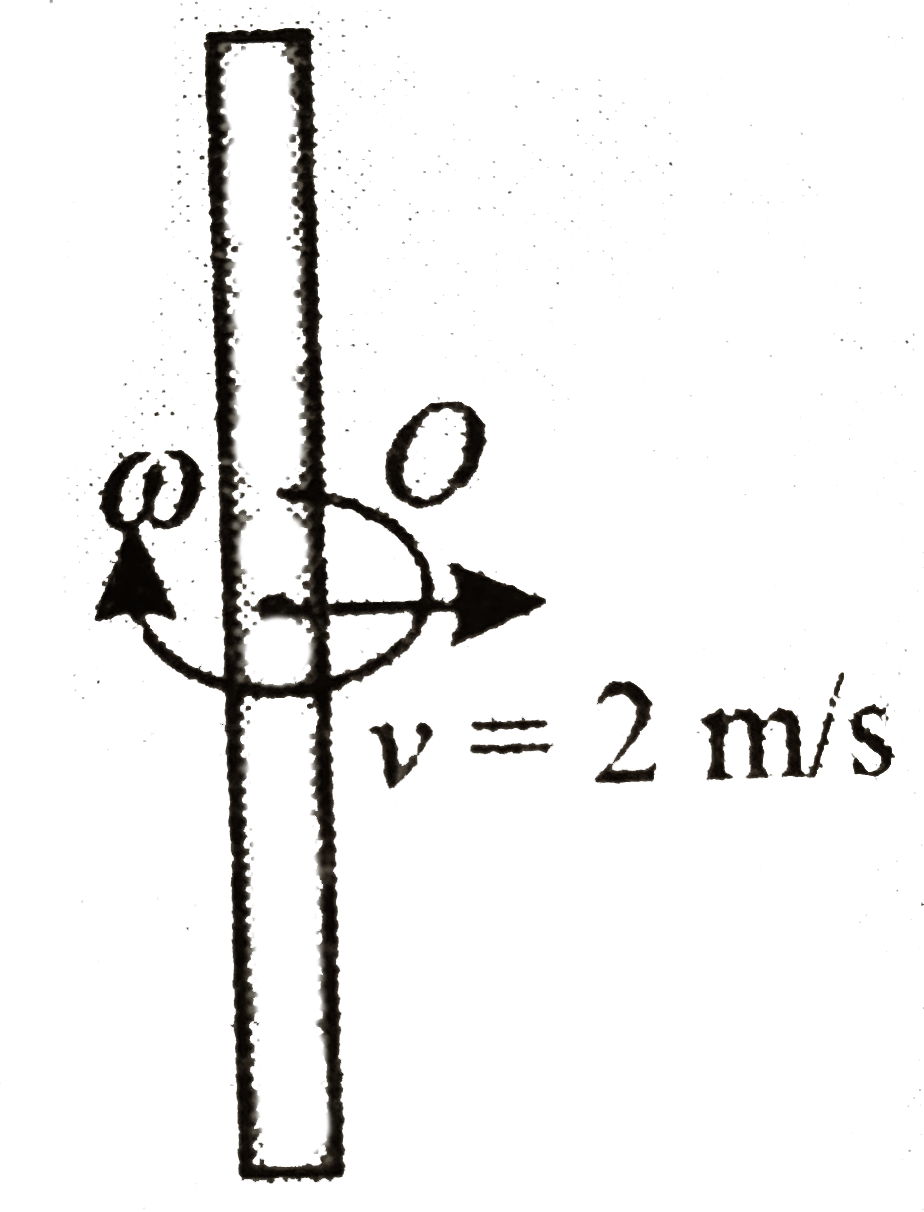
View Solution

