Shown in the figure is rod which moves with v=2ms−1 and rotates with ω=2πrads−1. Find the instantaneous axis of rotation.

Let P be a point passing through instantaneous axis of rotation.
Therefore vP=0
⇒|→vPO+→vO|=0
⇒vPO−vO=0⇒vPO=vO
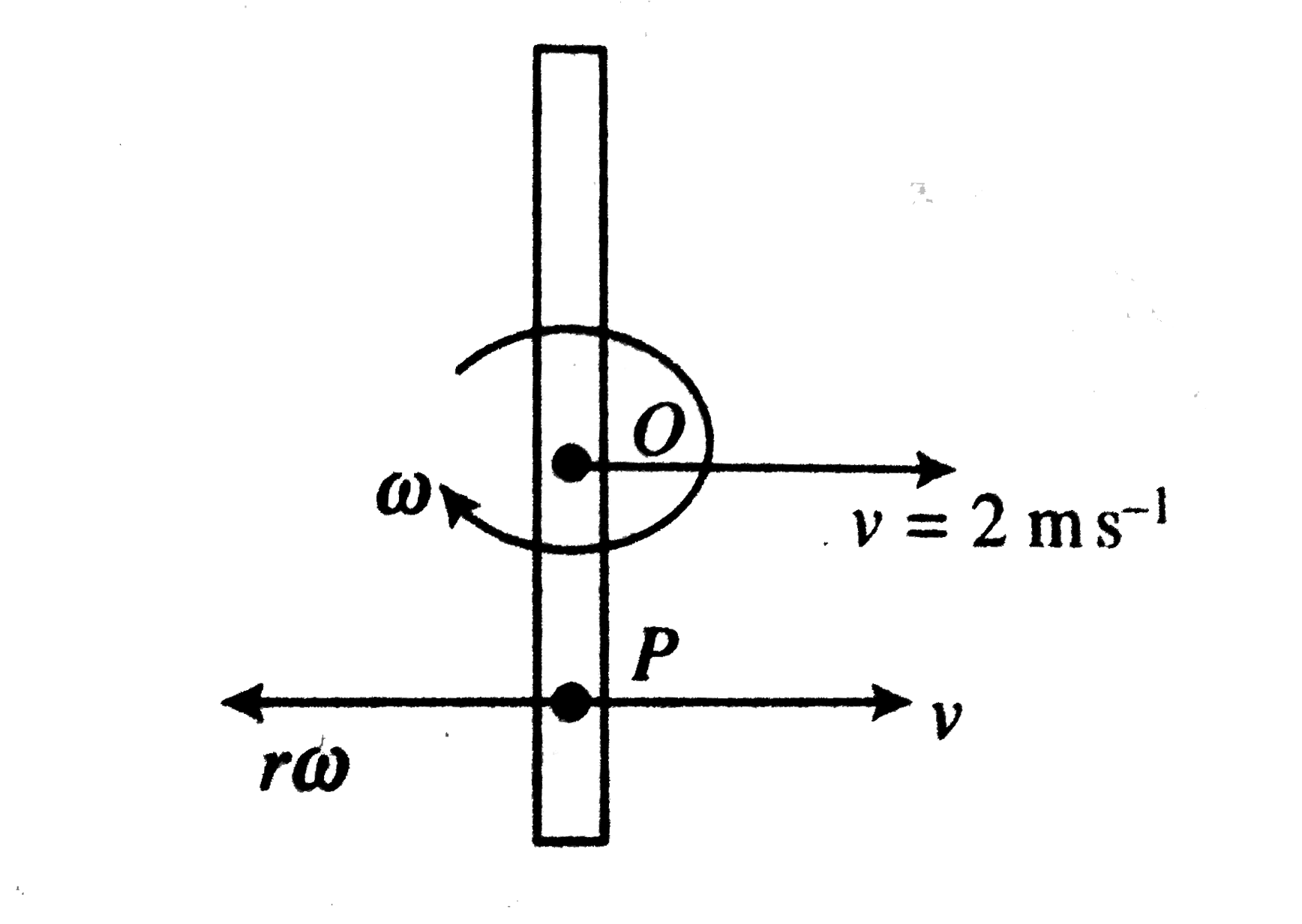
where v0=v and vPO=(OP)ω
⇒(OP)ω=v⇒OP=vω22π=1πm
Topper's Solved these Questions
- RIGID BODY DYNAMICS 1Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 1Exercise:Exercise 2.2
Explore 17 Videos
- RIGID BODY DYNAMICS 1Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 1Exercise:Exercise 2.3
Explore 15 Videos
- RIGID BODY DYNAMICS 1Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 1Exercise:Solved Examples
Explore 9 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBook:CENGAGE PHYSICSChapter:PROPERTIES OF SOLIDS AND FLUIDSExercise:INTEGER_TYPE
Explore 2 Videos
- RIGID BODY DYNAMICS 2Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 2Exercise:Interger
Explore 2 Videos
Similar Questions
As shown in the figure, a rod moves with v = 2 m/sec & rotates with ω=2π rad/sec. Find the point on the rod whose velocity is zero in this frame.

View SolutionA light rigid rod of length l is constrained to move in a vertical plane, so that its ends are along the x and y axes respectively. Find the instantaneous axis of rotation of the rod when it makes an angle θ with horizontal.

View Solution
Knowledge Check
Which of the following statements are correct for instantaneous axis of rotation?
AAcceleration of every point lying on the axis must be equal to zeroBVelocity of a point distance r from the axis is equal to rωCif moment of inertia of a body about the axis is I and angular velocity is (ω), then kinetic energy of the body is equal to Iω2/2DMoment of inertia of a body is least about nstantaneous axis of rotation among all the parallel axes.There is rod of length l. The velocities of its two ends are v1andv2 is opposite directions normal to the rod. The distance of the instantaneous axis of rotation from v1 is :
AzeroBv2v1+v2lCv1lv1+v2D1/2A rod of length l is given two velocities v1 and v2 in opposite directions at its two ends at right angles to the length. The distance of the instantaneous axis of rotation from v1 is
AzeroBv1v1+v2lCv2lv1+v2Dl2
The rod of length l=1m rotates with an angular velocity ω=2rads−1 an the point P moves with velocity v=1ms−1 and acceleration a=1ms−2. Find the velocity and acceleration of Q.

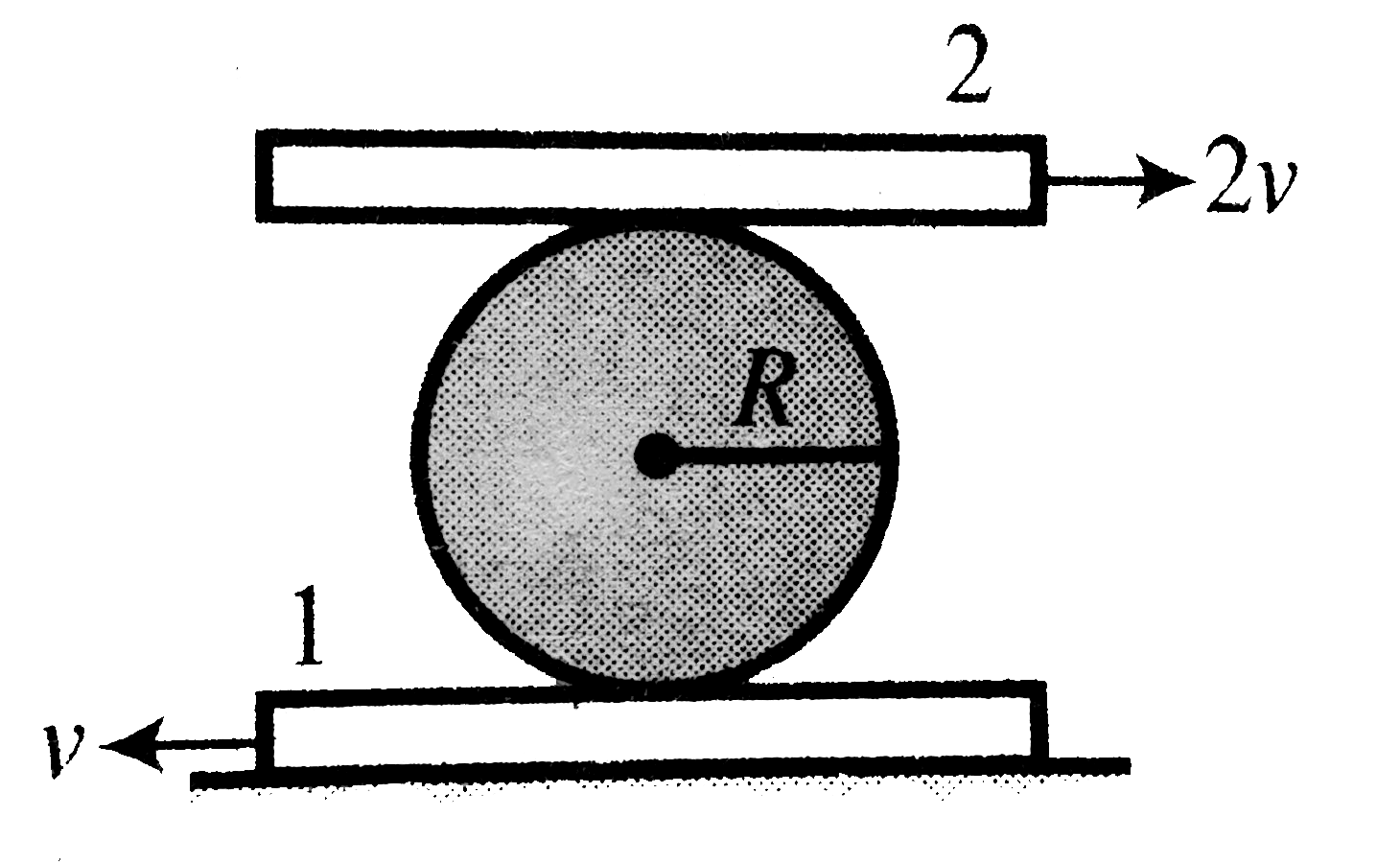
View SolutionA cylinder is rolling without sliding over two horizontal planks (surfaces) 1 and 2. If the velocities of the surfaces A and B are −vˆi and 2vˆi respectively, find the:
a. Position of instantaneous axis of rotation.
b. Angular velocity of the cylinder.
View SolutionA rod of length l is given two velocities v1 & v2 in opposite directions at its two ends at rigt angles to the length. The distance of the instantaneous axis of rotation from v1 is:
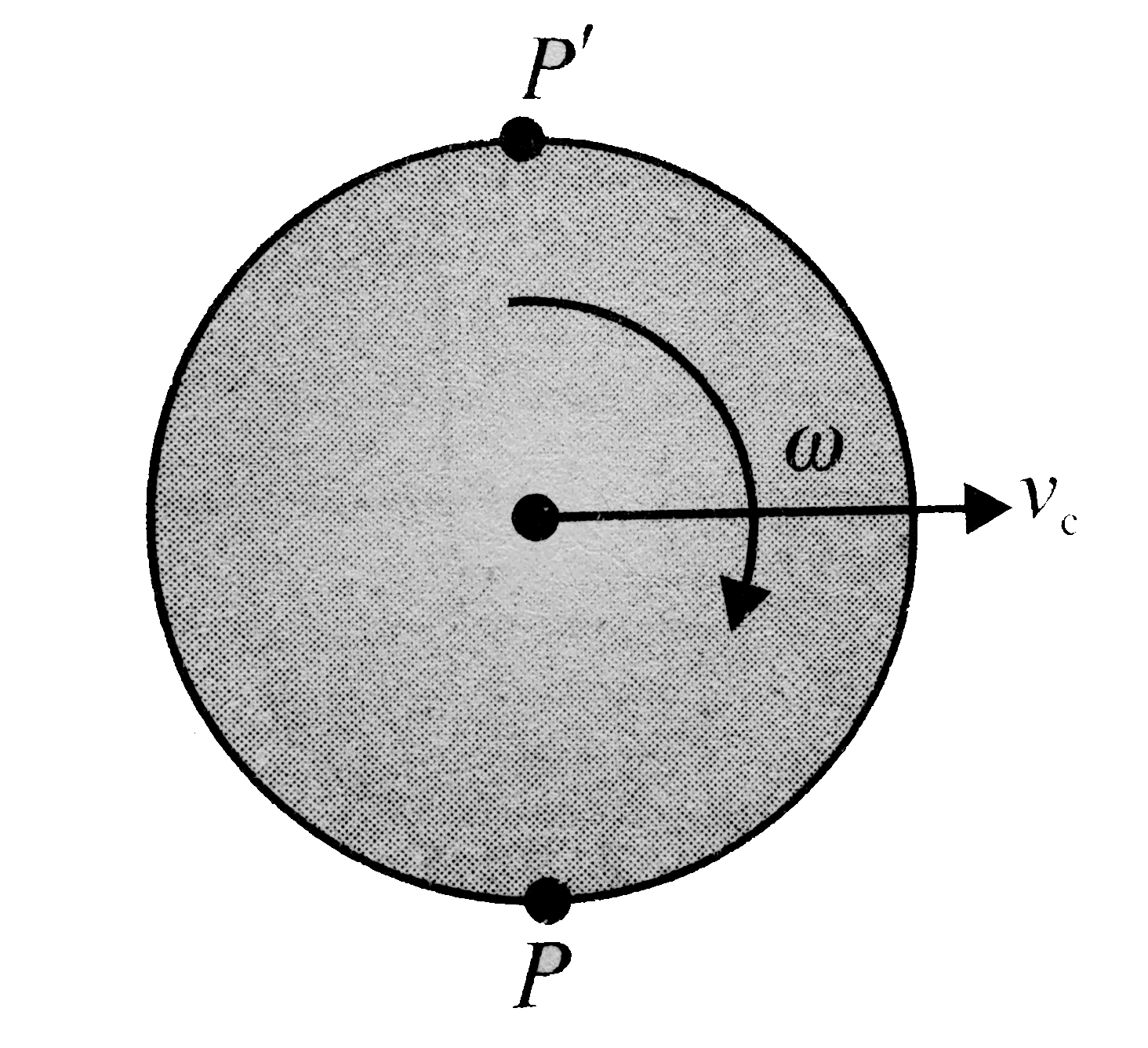
View SolutionA sphere is moving towards the positive x-axis with a velocity vc and rotates clockwise with angular speed ω shown in Fig. such that vc>ωR. The instantaneous axis of rotation will be
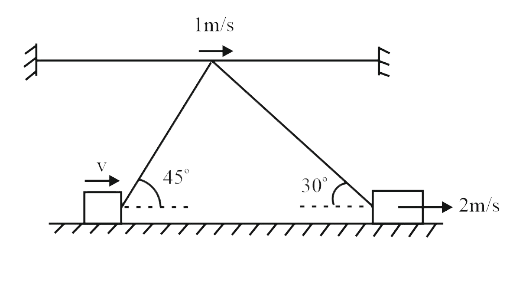
View SolutionConsider the following diagram in which an inextensible string connects two blocks passing via ring. The first block moves with a velocity of 2ms−1 and the second one moves with a velocity of vms−1. If the ring slides on horizontal rod then the value of v is (in ms−1)
View Solution

