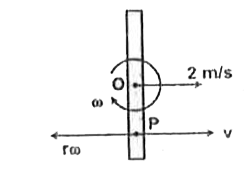
As shown in the figure, a rod moves with v = 2 m/sec & rotates with ω=2π rad/sec. Find the point on the rod whose velocity is zero in this frame.

vP=0
⇒ ∣→VPO+→vo=0
⇒ vPO−vO=0⇒ vPO=vo
where vO=v&vPO=(OP)ω
⇒ (OP)ω=v
⇒ OP=vω=22.π=1πm.
The point is located at 1π m down to the centre of mass.
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - FIITJEECHAPTER - ROTATIONAL MECHANICSEXERCISE - ASSIGNMENT PROBLEMS (SUBJECTIVE ) LEVEL - I
15 Videos
- ROTATIONAL MECHANICSBOOK - FIITJEECHAPTER - ROTATIONAL MECHANICSEXERCISE - ASSIGNMENT PROBLEMS (SUBJECTIVE ) LEVEL - II & III
15 Videos
- ROTATIONAL MECHANICSBOOK - FIITJEECHAPTER - ROTATIONAL MECHANICSEXERCISE - NUMERICALS BASED QUESTIONS
4 Videos
- PHYSICS PART2BOOK - FIITJEECHAPTER - PHYSICS PART2EXERCISE - Numerical Based Question Decimal Type
6 Videos
- SEMICONDUCTOR AND DEVICEBOOK - FIITJEECHAPTER - SEMICONDUCTOR AND DEVICEEXERCISE - SOLVED PROBLEMS Objective: Level-I
20 Videos
Similar Questions
Shown in the figure is rod which moves with v=2ms−1 and rotates with ω=2πrads−1. Find the instantaneous axis of rotation.

View SolutionThe rod AB oriented parallel to the x′ axis of the reference frame K′ moves in this frame with a velocity v′ along its y′ axis. In its turn, the frame K′ moves with a velocity V relative to the frame K as shown in figure. Find the angle θ between the rod and the x axis in the frame K.

View Solution
Knowledge Check
Three particles are situated on a light and rigid rod placed along Y-axis. If the system rotates about X-axis, the M.I. of the system is :
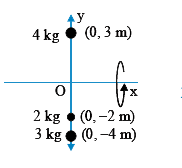 A92JB184JC276JD46J
A92JB184JC276JD46JA rod having length l and resistance R is moving with velocity v on a π shape conductor. Find the current in the rod.
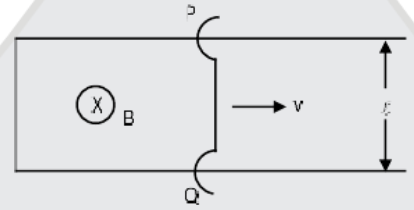 A(12)(BvlR)B(2BvlR)C(3BvlR)D(BvlR)
A(12)(BvlR)B(2BvlR)C(3BvlR)D(BvlR)
A uniform rod AB of mass m and length L rotates about a fixed vertical axis making a constant angle θ with it as shown in figure. The rod is rotated about this axis, so that point B the free end of the rod moves with a uniform speed V in the horizontal plane then the angular momentum of the rod about the axis is:A12mVLcosθB13mVLsinθCmVLsincosθDzero
A rod has length 'l' and mass per unit length linearly increases from λ to 2λ as shown in figure. Rod rotates with constant angular velocity ω in a gravity free space. Find the tension (in Newton) in the rod at its middle point. (take ωl=2m/secandλ=3kg/m)

View SolutionA midpoint of a thin uniform rod AB of mass m and length l is rigidly fixed to a rotation axle OO′ as shown in figure. The rod is set into rotation with a constant angular velocity ω. Find the resultant moment of the centrifugal forces of inertia relative to the point C in the reference frame fixed to the axle OO′ and to the end.

View SolutionA uniform rod of mass m and length L is fixed to an axis, making an angle θ with it as shown in the figure. The rod is rotated about this axis so that the free end of the rod moves with a uniform speed ‘v’. Find the angular momentum of the rod about the axis. Is the angular momentum of the rod about point A constant?

View SolutionThe rod of length l=1m rotates with an angular velocity ω=2rads−1 an the point P moves with velocity v=1ms−1 and acceleration a=1ms−2. Find the velocity and acceleration of Q.

View SolutionA conducting frame is placed in a horizontal plane as shown in the figure. The two sides are parallel and separated by a distance of 0.25 m. A massless conducting rod can slide without friction on the frame. The total resistance of the circuit is 40 Omega. The rod is connected to a 0.2 kg mass by a massless cord which passes over a massless and frictionless pulley. A uniform magnetic field of 2T points vertically upward. The voltage of the bettery is 100 V. Find the constant velocity in m//s with which the rod and mass eventually move.
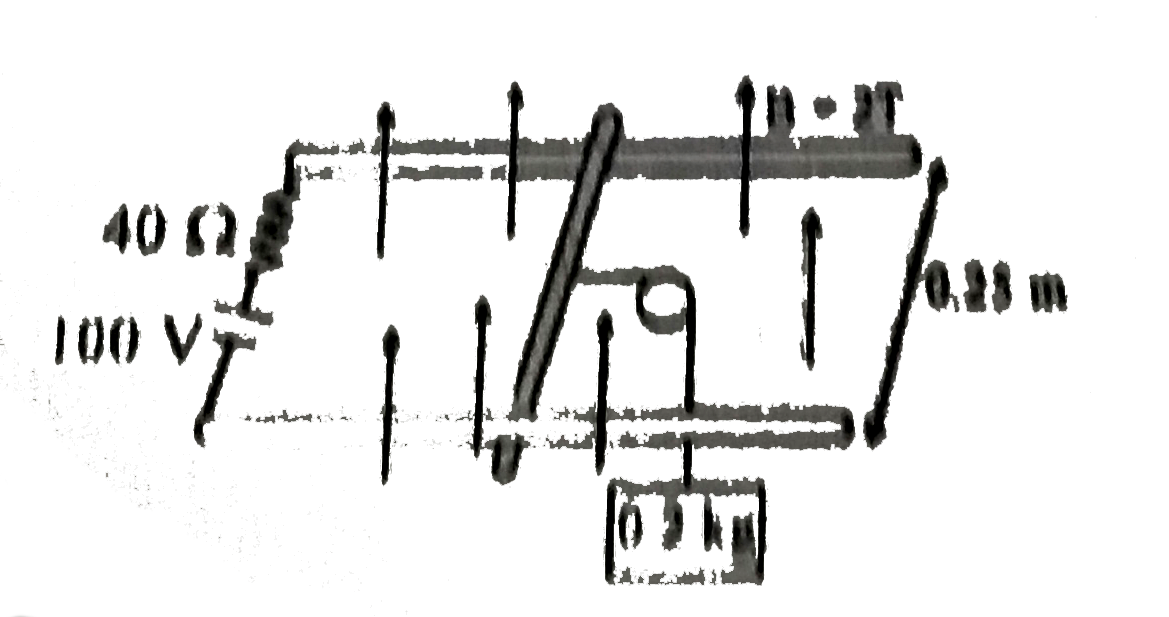
View Solution
