A bullet of mass m collides inelastically at the periphery of a disc of mass M and radius R, with a speed v as shown. The disc rotates about a fixed horizontal axis. Find the angular velocity of the disc bullet system just after the impact.

In this impact, the torque caused by the impulsive forces acting about the centr O is zero as for the system of bullet and disc impact force is internal force.
That is why we can conserve the angular momentum of the system about the axis passing through O just before and after the impact. The angular momentum of the system about O, is mvR=(I0)ω ...(1)
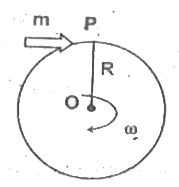
where I0 = M.I. of the system about O=(Idisc)0+(Ibullet)0
I0=12MR2+mR2=(M+2m2)R2 ...(2)
Using (A1) & (2) we obtain
ω=vR(M2m+1)
Topper's Solved these Questions
- ROTATIONAL MECHANICSBook:FIITJEEChapter:ROTATIONAL MECHANICSExercise:ASSIGNMENT PROBLEMS (SUBJECTIVE ) LEVEL - I
Explore 15 Videos
- ROTATIONAL MECHANICSBook:FIITJEEChapter:ROTATIONAL MECHANICSExercise:ASSIGNMENT PROBLEMS (SUBJECTIVE ) LEVEL - II & III
Explore 15 Videos
- ROTATIONAL MECHANICSBook:FIITJEEChapter:ROTATIONAL MECHANICSExercise:NUMERICALS BASED QUESTIONS
Explore 4 Videos
- PHYSICS PART2Book:FIITJEEChapter:PHYSICS PART2Exercise:Numerical Based Question Decimal Type
Explore 6 Videos
- SEMICONDUCTOR AND DEVICEBook:FIITJEEChapter:SEMICONDUCTOR AND DEVICEExercise:SOLVED PROBLEMS Objective: Level-I
Explore 20 Videos
Similar Questions
A disc of mass M and Radius R is rolling with an angular speed ω on the horizontal plane. The magnitude of angular momentum of the disc about origin is:

View SolutionA particle of mass m strikes elastically with a disc of radius R, with a velocity →v as shown in the figure. If the mass of the disc is equal to that of the particle and the surface of the contact is smooth, find the velocity of the disc just after the collision.

View Solution
Knowledge Check
A point mass m collides with a disc of mass m and radius R resting on a rough horizontal surface as shown . Its collision is perfectly elastic. Find angular velocity of the disc after pure rolling starts
 A(2u3R)B(3u3R)C(5u3R)D(2u5R)
A(2u3R)B(3u3R)C(5u3R)D(2u5R)A uniform disc of mass M and radius R is hinged at its centre C. A force F is applied on the disc as shown. At this instant, the angular acceleration of the disc is
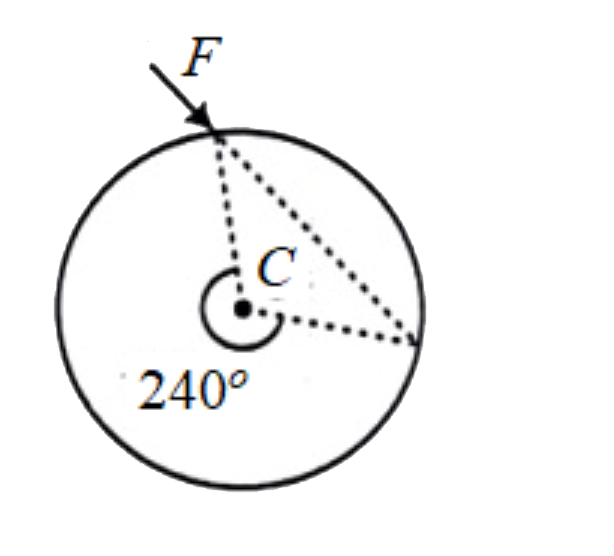 A√3FMRBFMRC2√3FMRDF2MR
A√3FMRBFMRC2√3FMRDF2MRA disc of mass m and radius R moves in the x−y plane as shown in Fig. The angular momentum of the disc about the origin O at the instant shown is
 A−52mR2ωˆkB73mR2ωˆkC−92mR2ωˆkD52mR2ωˆk
A−52mR2ωˆkB73mR2ωˆkC−92mR2ωˆkD52mR2ωˆk
A disc of mass M and radius R is rolling with angular speed w on horizontal plane as shown. The magnitude of angular momentum of the disc about the origin O is :

View SolutionA uniform disc of mass M and radius R is hinged at its centre C . A force F is applied on the disc as shown . At this instant , angular acceleration of the disc is

View SolutionA man of mass m stands on a horizontal platform in the shape of a disc of mass m and radius R, pivoted on a vertical axis through its centre about which it can freely rotate. The man starts to move around the centre of the disc in a circle of radius r with a velocity v relative to the disc. Calculate the angular velocity of the disc.

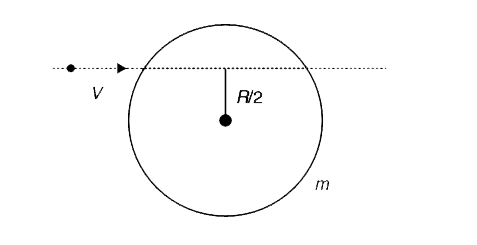
View SolutionA disc of mass m and radius R lies flat on a smooth horizontal table. A particle of mass m, moving horizontally along the table, strikes the disc with velocity V while moving along a line at a distance R2 from the centre. Find the angular velocity acquired by the disc if the particle comes to rest after the impact.
View SolutionA disc of mass M and radius R is rolling with angular speed ω on a horizontal plane. The magnitude of angular momentum of the disc about a point on ground along the line of motion of disc is :
View Solution