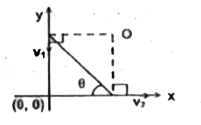
A light rigid rod of length l is constrained to move in a vertical plane, so that its ends are along the x and y axes respectively. Find the instantaneous axis of rotation of the rod when it makes an angle θ with horizontal.

If we drop perpendiculars upon →v1and→v2, they meet at O. Therefore, O is the instantaneous point of rotation and the axis passing through and perpendicular to the plane of rotation is known as axis of rotation.
The coordinates of O is given as l cos θ and l sin θ respectively.
⇒ 0=(lcosθ,lsinθ)
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - FIITJEECHAPTER - ROTATIONAL MECHANICSEXERCISE - ASSIGNMENT PROBLEMS (SUBJECTIVE ) LEVEL - I
15 Videos
- ROTATIONAL MECHANICSBOOK - FIITJEECHAPTER - ROTATIONAL MECHANICSEXERCISE - ASSIGNMENT PROBLEMS (SUBJECTIVE ) LEVEL - II & III
15 Videos
- ROTATIONAL MECHANICSBOOK - FIITJEECHAPTER - ROTATIONAL MECHANICSEXERCISE - NUMERICALS BASED QUESTIONS
4 Videos
- PHYSICS PART2BOOK - FIITJEECHAPTER - PHYSICS PART2EXERCISE - Numerical Based Question Decimal Type
6 Videos
- SEMICONDUCTOR AND DEVICEBOOK - FIITJEECHAPTER - SEMICONDUCTOR AND DEVICEEXERCISE - SOLVED PROBLEMS Objective: Level-I
20 Videos
Similar Questions
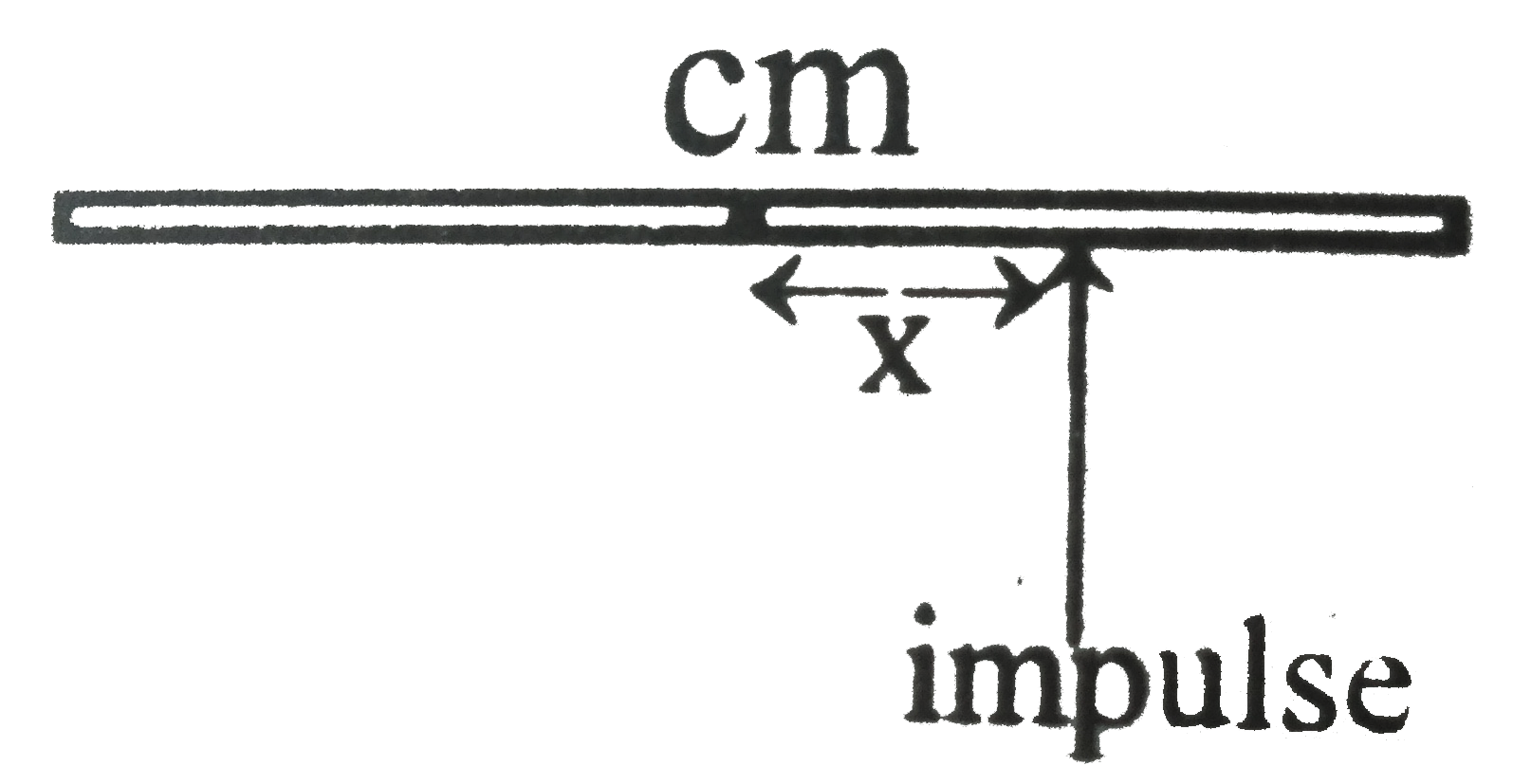
A uniform rod of length l is given an impulse at right angles to its length as shown. Find the distance of instantaneous centre of rotation from the centre of the rod.
 .
.
View SolutionA rod od length l is moving in a vertical plane (x−y) when the owest point A of the rod is moved with a velociy v. find the a angular velocity of the rod and b velocity of the end B.

View Solution
Knowledge Check
A rod of length l is given two velocities v1 and v2 in opposite directions at its two ends at right angles to the length. The distance of the instantaneous axis of rotation from v1 is
AzeroBv1v1+v2lCv2lv1+v2Dl2A rod of length l is given two velocities v1 & v2 in opposite directions at its two ends at rigt angles to the length. The distance of the instantaneous axis of rotation from v1 is:
AzeroBv1v1+v2lCv2lv1+v2Dl2A slender uniform rod of mass M and length l is pivoted at one ens so that it can rotate in a vertical plane, Fig. There is negligible friction at the pivot. The free end is held vertically above the pivot and then released. The angular acceleration of the rod when it makes an angle θ with the vertical is
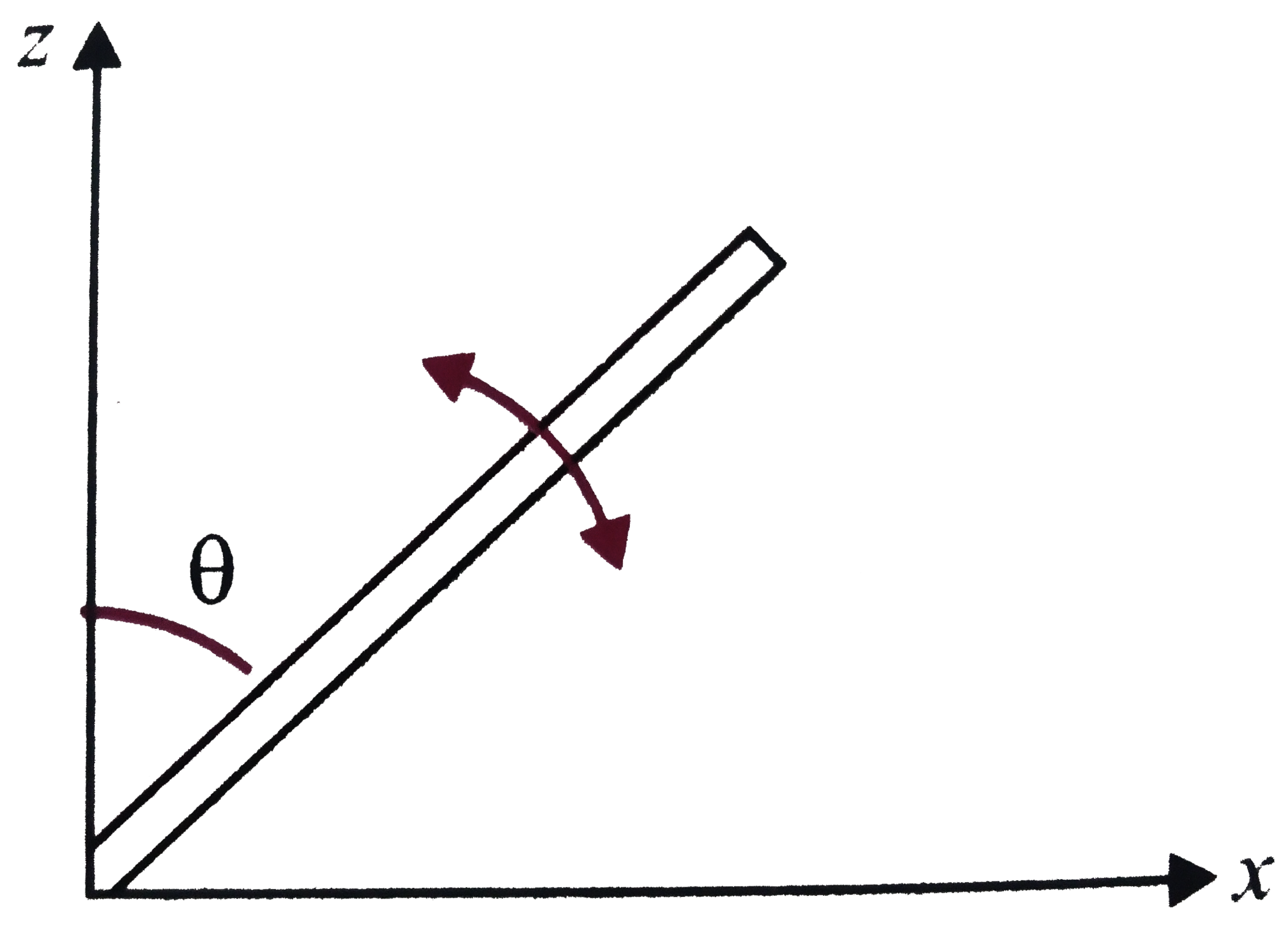 A3g2lcosθB2g3lcosθC3g2lsinθD2g3lsinθ
A3g2lcosθB2g3lcosθC3g2lsinθD2g3lsinθ
Figure shows a rod of length l resting on a wall and the floor. Its lower end A is pulled towards left with a constant velocity u. As a result of this, end A starts moving down along the wall. Find the velocity of the other end B downward when the rod makes an angle θ with the horizontal.

View SolutionAB is a mass less rigid rod of length 2l. It is free to rotate in vertical plane about a horizontal axis passing through its end A. Equal point masses (m each) are stuck at the centre C and end Bof the rod. The rod is released from horizontal position. Write the tension in the rod when it becomes vertical.

View SolutionA thin rod MN free to rotation in the vertical plane about the fixed end N is held horizontal when the end M is released the speed of this end when the rod makes an angle α with the horizontal will be proportional to : (see figure)

View Solution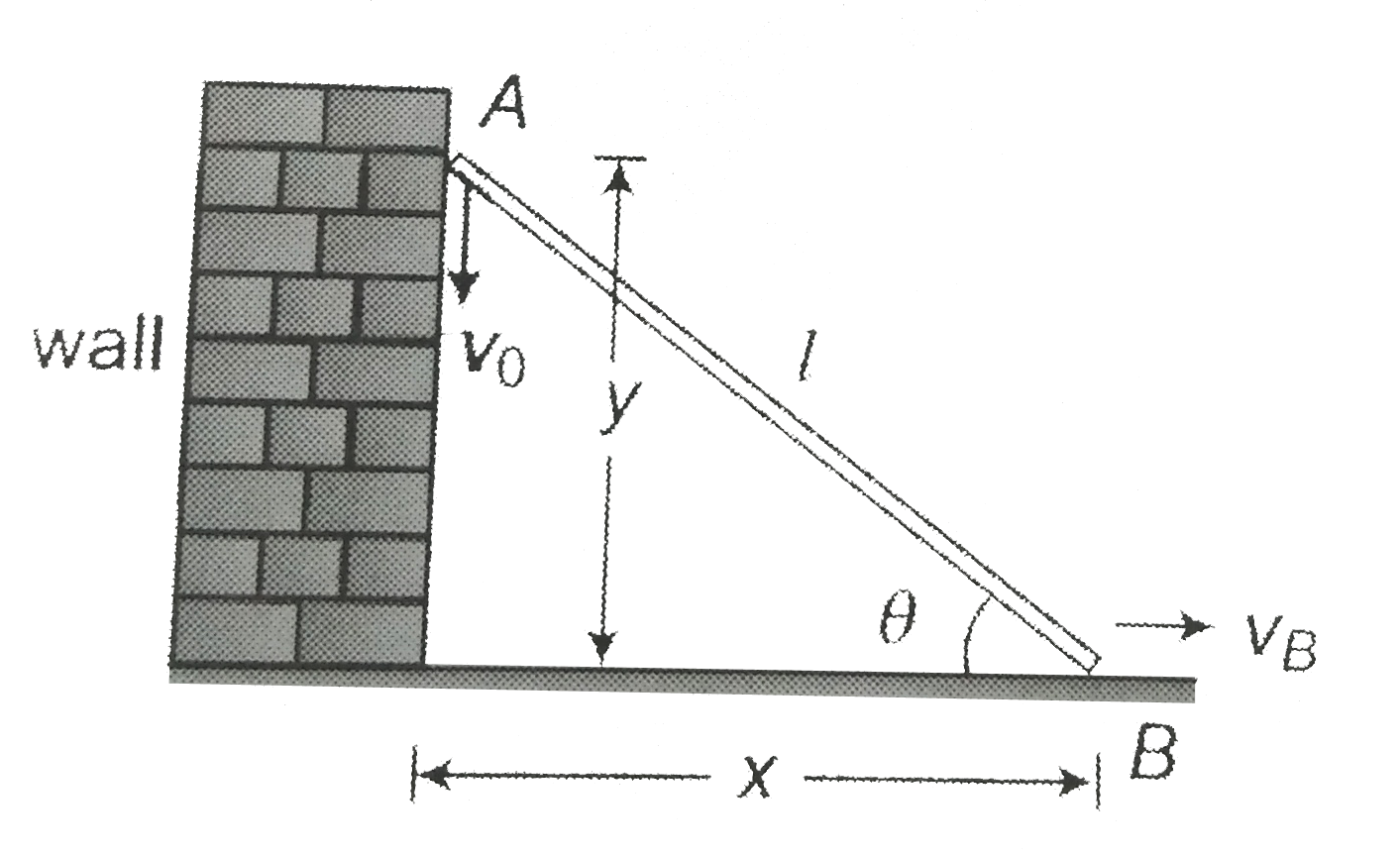
Consider a rod of length l resting on a wall and the floor. If the velocity of the upper end of a rod A is v0 in downward direction, find the velocity of the lower end B at this iinstant, when the rod makes an angle θ with horizontal
View SolutionA uniform rod of mass m and length l0 is rotating with a constant angular speed ω about a vertical axis passing through its point of suspension. Find the moment of inertia of the rod about the axis of rotation if it make an angle θ to the vertical (axis of rotation).
View Solution
