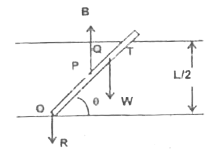
A uniform rod of length $L$ pivoted at the bottom of a pond of depth $L / 2$ stays in stable equilibrium as shown in the figure.

Find the angle $θ$ if the density of the material of the rod is half of the density of water.

Video Solution

Text Solution

Verified by Experts

(a) Weight of the rod W = LA $ρ$ g
(A = area of cross section, $ρ$ = density of material)
Submerged length of the rod
$O T = \frac{L}{2 sin θ}$
Buoyant force, $B = (\frac{L}{2 sin θ}) A ρ_{w} g$
(from Archimedies principle) ( $ρ_{w}$ = density of water)
This acts at P, where $O P = \frac{O T}{2} = \frac{l}{4 sin θ}$
Balancing torque about O
$W . O Q cos θ = B . O P cos θ$
$(L A ρ g) L / 2 = (\frac{L}{2 sin θ}) A ρ_{w} g (\frac{L}{4 sin θ})$
${sin}^{2} θ = \frac{ρ_{w}}{4 ρ}$
$\Rightarrow {sin}^{2} θ = 1 / 2 \Rightarrow θ = 45^{\circ}$

(b) Also, balancing forces
R + W = B
$R = B - W = \frac{ρ A ρ_{w} g}{2 sin θ} - L A ρ g$
$= L A ρ g [\frac{1}{sin θ} - 1] (∵ ρ_{w} = 2 ρ)$
$= (\sqrt{2} - 1) m g$

Updated on:21/07/2023