A uniform rod of length l is spinning with an angular velocity ω=2vl while its centre of mass moves with a velocity v. Find the velocity of the end of the rod.

Velocity of end A →vA=→cA,C=→vC
Hence the velocity of A is
vA=√v2AC+v2C+2vACvCcosθ
we know vC=V,VAC=l2.ω and θ=90∘+30∘=120∘
Hence vA=√v2+l2ω24+lvωcos120∘

But ω=2vl
vAC=l2ω=l2(2vl)=v
which gives vA=v
Let →vA make angle ϕ with the direction of →vC. Then
ϕ=tan−1(vsinθ)vACcosθ+vC
we get ϕ=tan−1(vsin120∘)vcos120∘+v=π2
Topper's Solved these Questions
- RIGID BODY DYNAMICS 1Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 1Exercise:Solved Examples
Explore 9 Videos
- RIGID BODY DYNAMICS 1Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 1Exercise:Exercise 2.1
Explore 6 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBook:CENGAGE PHYSICSChapter:PROPERTIES OF SOLIDS AND FLUIDSExercise:INTEGER_TYPE
Explore 2 Videos
- RIGID BODY DYNAMICS 2Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 2Exercise:Interger
Explore 2 Videos
Similar Questions
A uniform rod of lengh l moving with a downward velocity v0 strikes a peg P. If the coefficient of restitutioin of impact is e, find the velocity of CM of the rod just after impact.

View SolutionA rod od length l is moving in a vertical plane (x−y) when the owest point A of the rod is moved with a velociy v. find the a angular velocity of the rod and b velocity of the end B.

View Solution
Knowledge Check
A uniform rod AB of length l rotating with an angular velocity ω while its centre moves with a linear velocity v=ωl6 If the end A of the rod is suddenly fixed, the angular velocity of
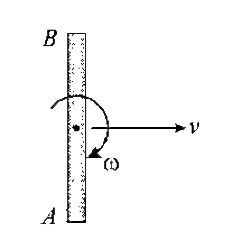 A34ωBω3Cω2D23ω
A34ωBω3Cω2D23ωA uniform rod of mass m and length l is rotating with constant angular velocity ω about an axis which passes thorugh its one end and perpendicular to the length of rod. The area of cross section of the rod is A and its Young's modulus is y. Neglect gravity. The strain at the mid point of the rod is:
Amn2l8AyB3mω2l8AyC3mω2l4AyDmω4AyIn the figure shown the end A of the rod of length L is being pushed down parallel to the inclined surface with a velocity =v let the velocity of end B=u and the angular velocity of the rod = ω then
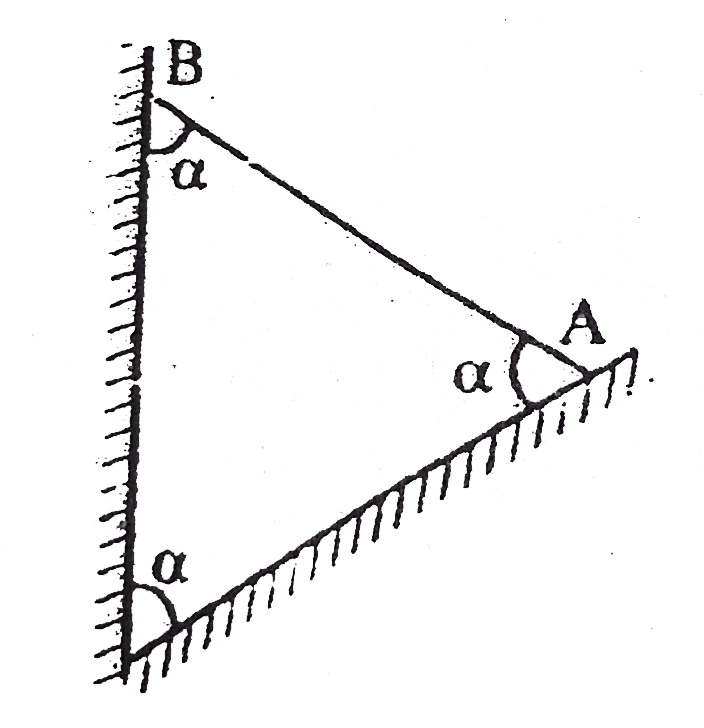 Au=vcosα (upward)Bu=v (downwards)Cω=vsinα/LDω=2vsinα/L
Au=vcosα (upward)Bu=v (downwards)Cω=vsinα/LDω=2vsinα/L
The rod of length l=1m rotates with an angular velocity ω=2rads−1 an the point P moves with velocity v=1ms−1 and acceleration a=1ms−2. Find the velocity and acceleration of Q.

View SolutionA rod PQ of length l is rotating about end P, with an angular velocity ω. Due to electrifugal forceed the free electrons in the rod move toward the end Q and an emf is created. Find the induced emf.

View SolutionA rod of length l is placed perpendicular to a long wire carrying current i. The rod is moved parallel to the wire with a velocity v. Find the emf induced in the rod, if its nearest end is at a distance a from the wire.

View SolutionA rod of length l is placed perpendicular to a long wire carrying current i. The rod is moved parallel to the wire with a velocity v. Find the emf induced in the rod, if its nearest end is at a distance ‘a’ from the wire.
View SolutionA uniform rod of mass m and length l rotates in a horizontal plane with an angular velocity ω about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is
View Solution

