
A rod of length 1 m rotates in the xy plane about the fixed point O in the anticlockwise sense, as shown in figure with velocity ω=a+bt where a=10rads−1 and b=5rads−2. The velocity and acceleration of the point A at t=0 is
+10ˆims−1 and +5ˆims−2
+10ˆjms−1 and (−100ˆi+5ˆj)ms−2
−10ˆjms−1 and (100ˆi+5ˆj)ms−2
−10ˆjms−1 and −5ˆjms−1
The correct Answer is:B
ω=10+5t
α=dωdt=5
At t=0,ω=10rad/s
and α=5rad/s2⇒r=OA=1m
v=(rω)ˆj=(10ˆj)m/s
a=(rα)ˆj−(rω2)ˆi
=(−100ˆi+5ˆj)m/s2
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 2 Multiple Correct
36 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 2
1 Video
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 1 Subjective
32 Videos
- ROTATIONBOOK - DC PANDEYCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEYCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions
17 Videos
Similar Questions
The rod of length l=1m rotates with an angular velocity ω=2rads−1 an the point P moves with velocity v=1ms−1 and acceleration a=1ms−2. Find the velocity and acceleration of Q.
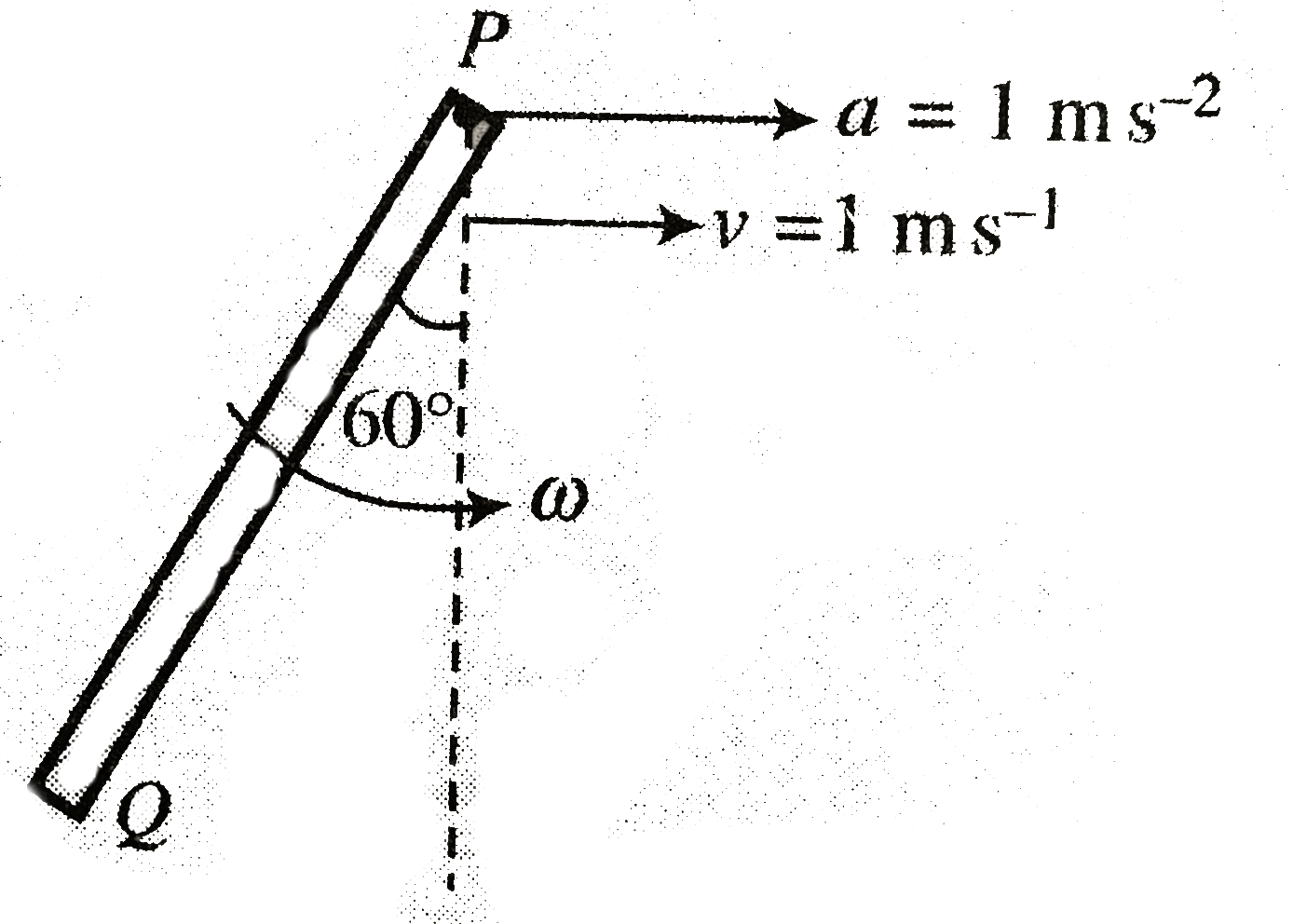
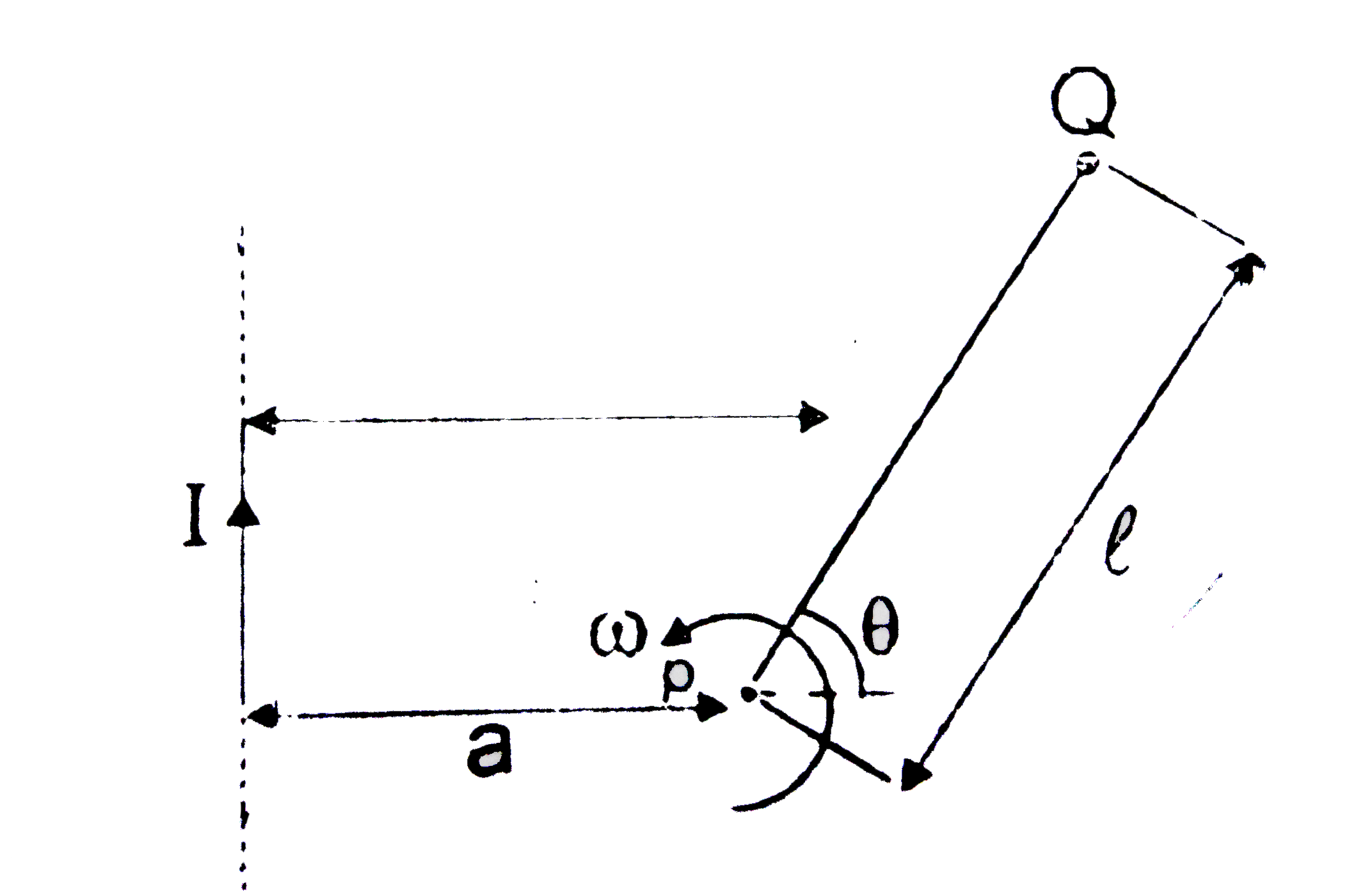
View SolutionIn the figure shown a long conductor carries constant current I. A rod PQ of length l is in the plane of the rod.The rod is rotated about point P with constant angular velocity ω as shown in the figure.Find the e.m.f induced in the rod in the position shown.Indicate which points is at high potential.
View Solution
Knowledge Check
the angular velocity omega of a particle varies with time t as ω=5t2+25rads. the angular acceleration of the particle att=1s is
A10rads2B5rads2CZeroD3rads2A rod OA of length l is rotating (about end O) over a conducting ring in crossed magnetic field B with constant angular velocity ω as shown in figure.
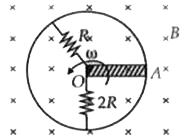 ACurrent flowing through the rod is 3Bωl24RBMagnetic force acting on the rod is 3B2ωl34RCTorque due to magnetic force acting on the rod is 3B2ωl48RDMagnitude of external force that acts perpendicularly at the end of the rod of maintain the constant angular speed is 3B2ωl38R
ACurrent flowing through the rod is 3Bωl24RBMagnetic force acting on the rod is 3B2ωl34RCTorque due to magnetic force acting on the rod is 3B2ωl48RDMagnitude of external force that acts perpendicularly at the end of the rod of maintain the constant angular speed is 3B2ωl38RThe angular velocity of a particle is given by the equation ω=2t2+5rads−1. The instantaneous angular acceleration at t=4 s is
A16rads−2B19rads−2C10rads−2D12rads−2
A conducting rod of length l is rotating with constant angular velocity ω about point O in a uniform magnetic field B as shown in the figure . What is the emf induced between ends P and Q ?

View SolutionTwo solid bodies rotate about stationary mutually perpendicular intersecting axes with constant angular velocities ω1=3.0rad/s and ω2=4.0rad/s. Find the angular velocity and angular acceleration of one body relative to the other.
View SolutionA rod of mass m and length l is rotating about a fixed point in the ceiling with an angular velocity ω as shown in the figure. The rod maintains a constant angle θ with the vertical.
What is the rate of change of angular momentum of the rod ?
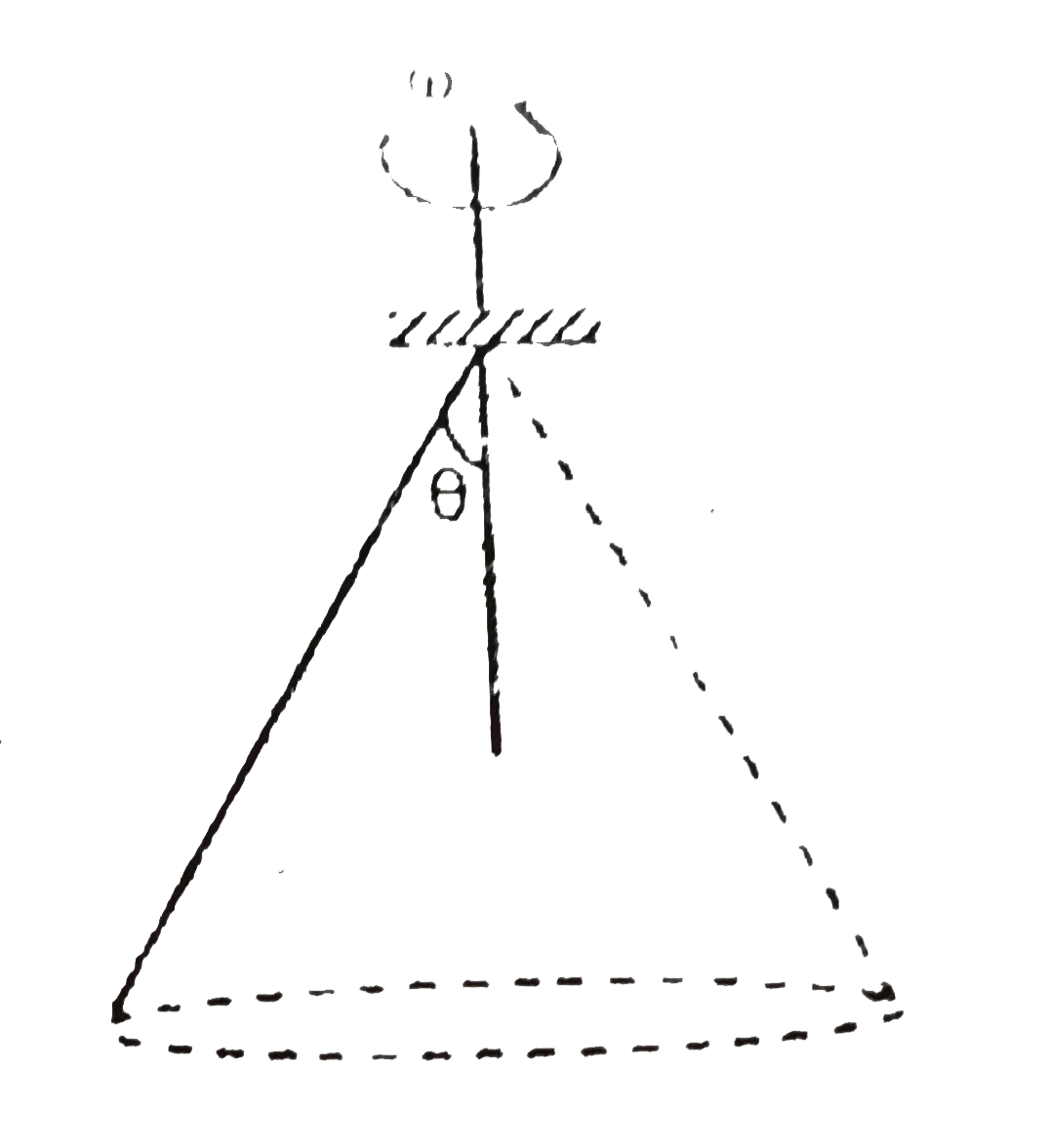
View SolutionA rod of mass m and length l is rotating about a fixed point in the ceiling with an angular velocity ω as shown in the figure. The rod maintains a constant angle θ with the vertical.
What angle will the rod make with the vertical
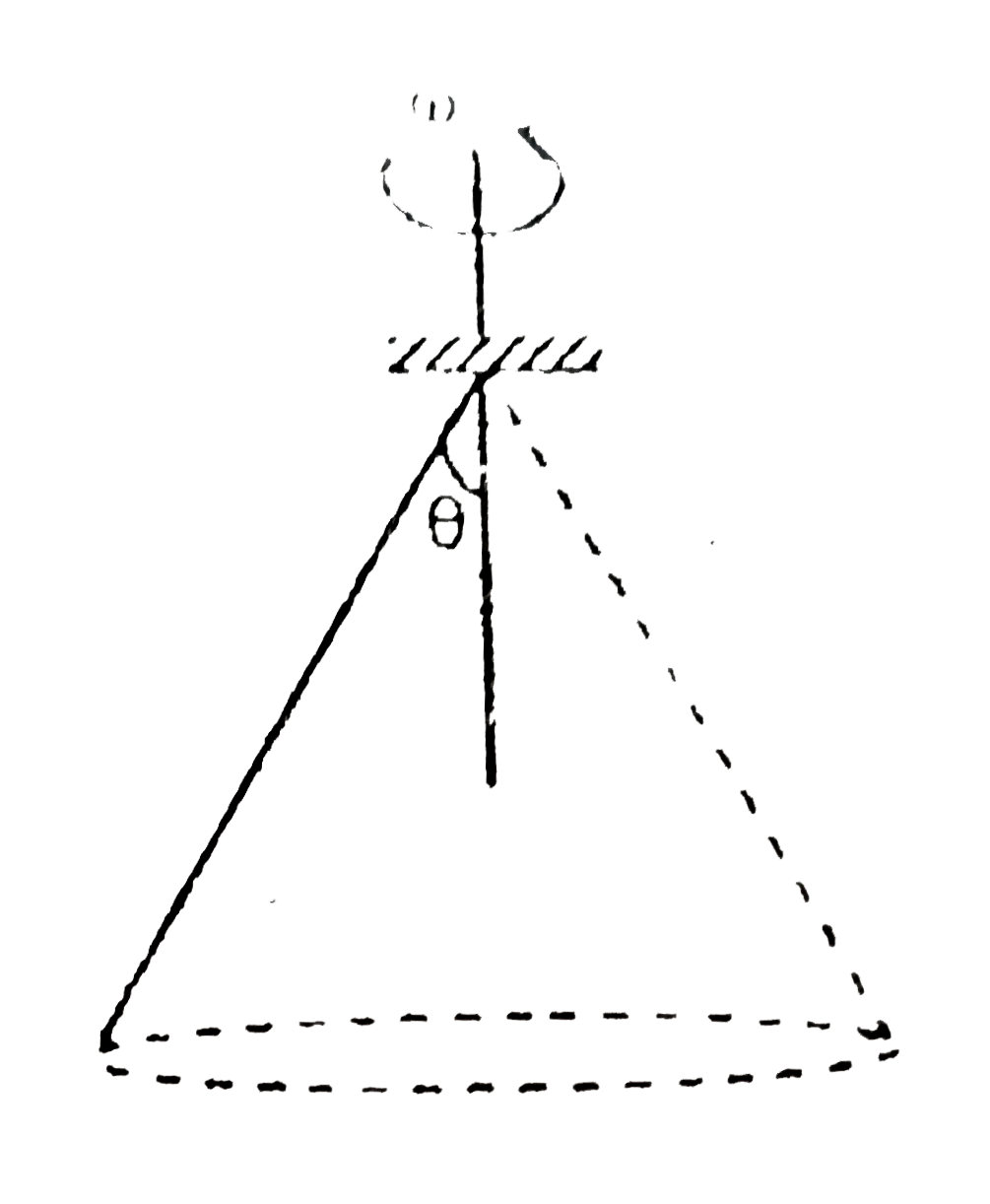
View SolutionA rod of mass m and length l is rotating about a fixed point in the ceiling with an angular velocity ω as shown in the figure. The rod maintains a constant angle θ with the vertical.
What will be the horizontal component of angular momentum of the rod about the point of suspension in terms of m, ω, l and θ.
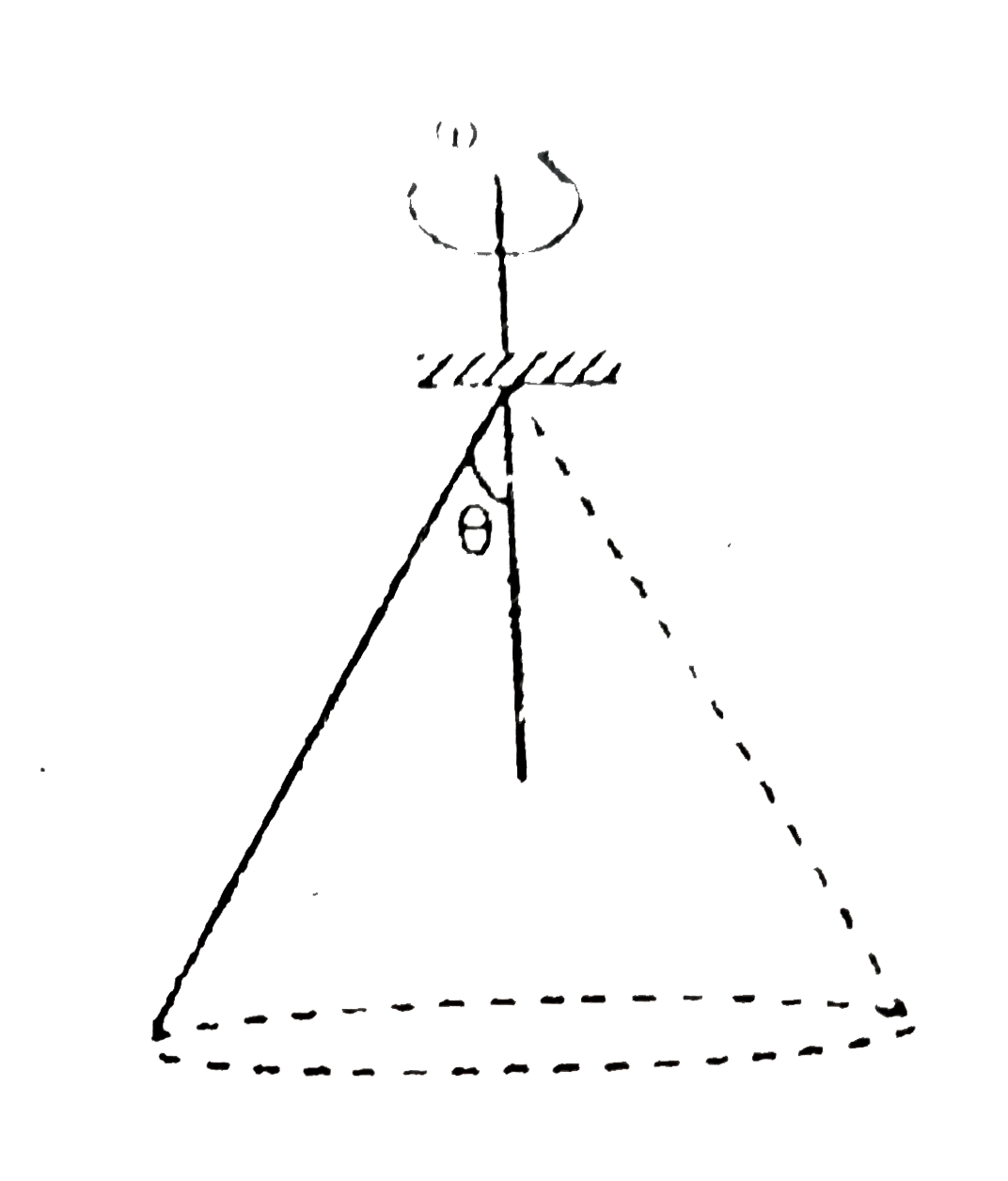
View Solution
