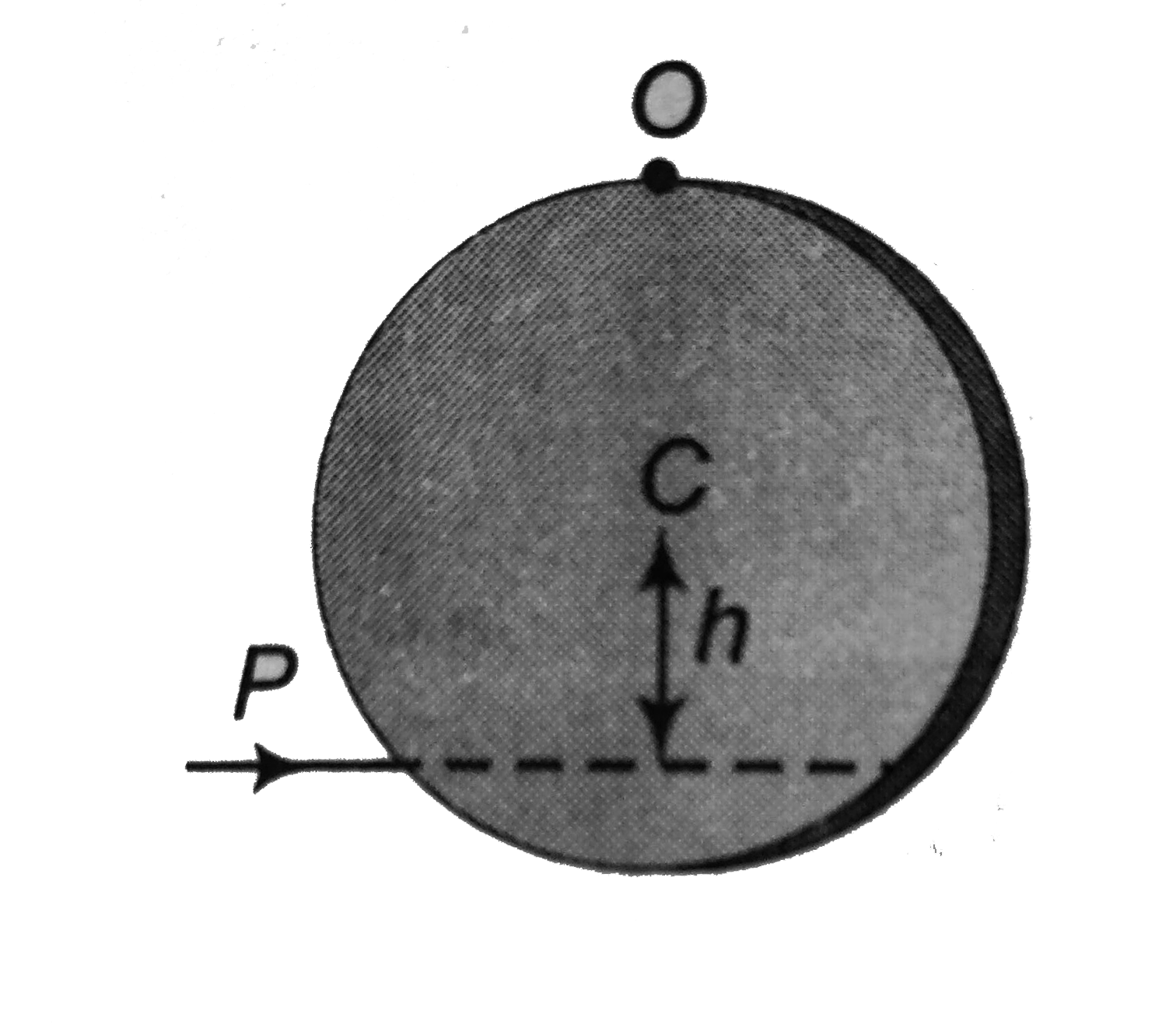
A uniform circular disc of radius R is placed on a smooth horizontal surface with its plane horizontal and hinged at circumference through point O as shown . An impulse P is applied at a perpendicular distance h from its centre C. The value of h so that the impulse due to hinge is zero, is
R
R/2
R/3
R/4
The correct Answer is:B

ω=angular impulseI (about O) ltbr =P(R+h)32mR2
Now, VCOM=Rω=PR(R+h)32mR2
P+PHinge=mvCOM=mpR(R+h)32mR2
solving, this equation we get h=R2
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 2 Multiple Correct
36 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 2
1 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 1 Subjective
32 Videos
- ROTATIONBOOK - DC PANDEYCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEYCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions
17 Videos
Similar Questions
A uniform sphere is placed on a smooth horizontal surface and a horizontal force F is applied on it at a distance h above the surface. The acceleration of the centre :
View SolutionA uniform solid sphere of mass M and radius R is placed on a smooth horizontal surface. It is given a horizontal impulse J at a height h above the centre of mass and sphere starts rolling. Then the value of h and speed of ccentre of mass are
View Solution
Knowledge Check
A disc having radius r=2m is placed on smooth horizontal surface. Velocity of point A and B is given as shown in fig. Distance between point O and axis of rotation at the particular instant is
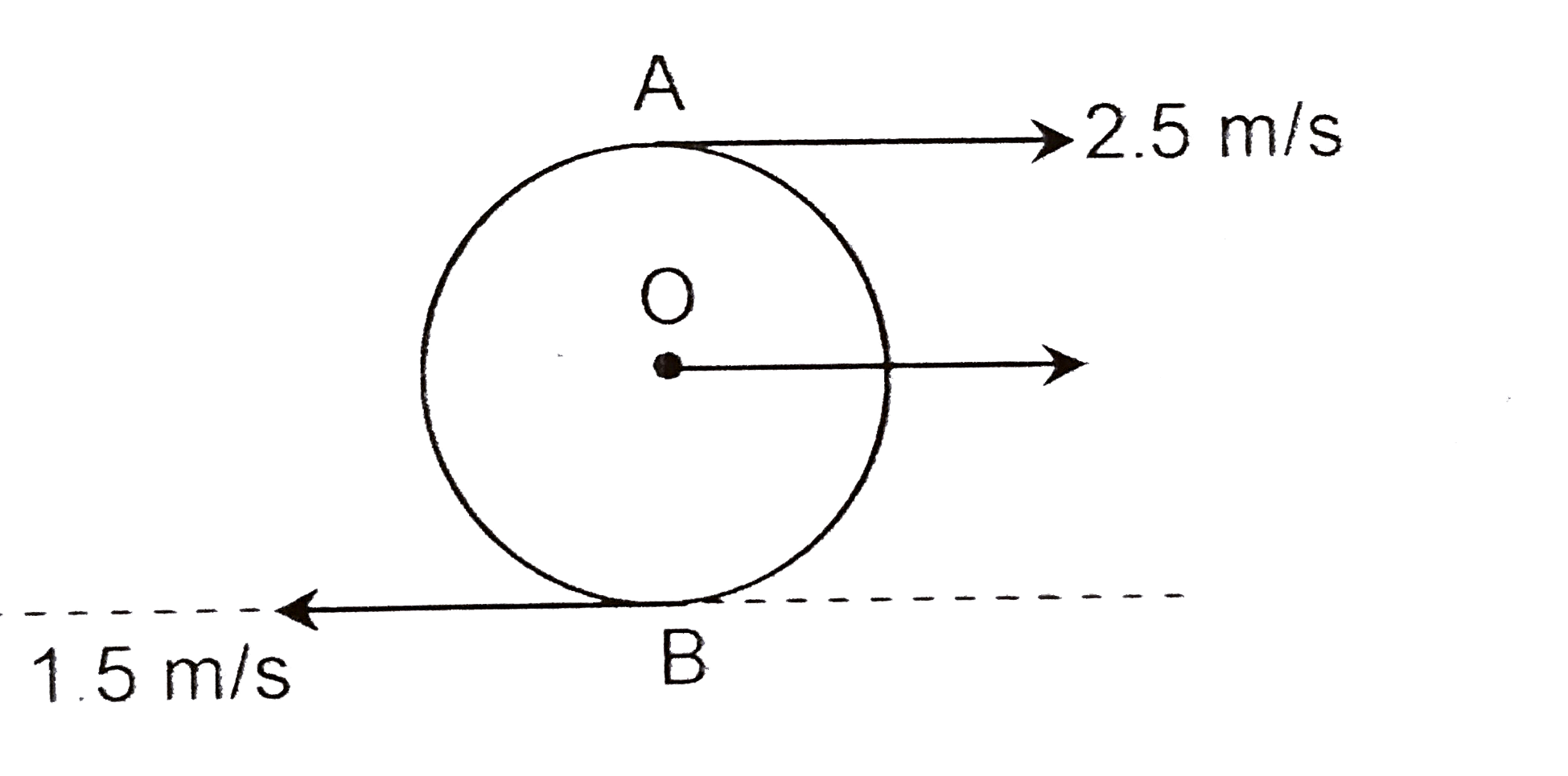 A1mB0.5mC0.25mD2m
A1mB0.5mC0.25mD2mA uniform circular disc of radius r is placed on a rough horizontal surface and given a linear velocity v0 and angular velocity ω0 as shown. The disc comes to rest after moving some distance to the right. It follows that
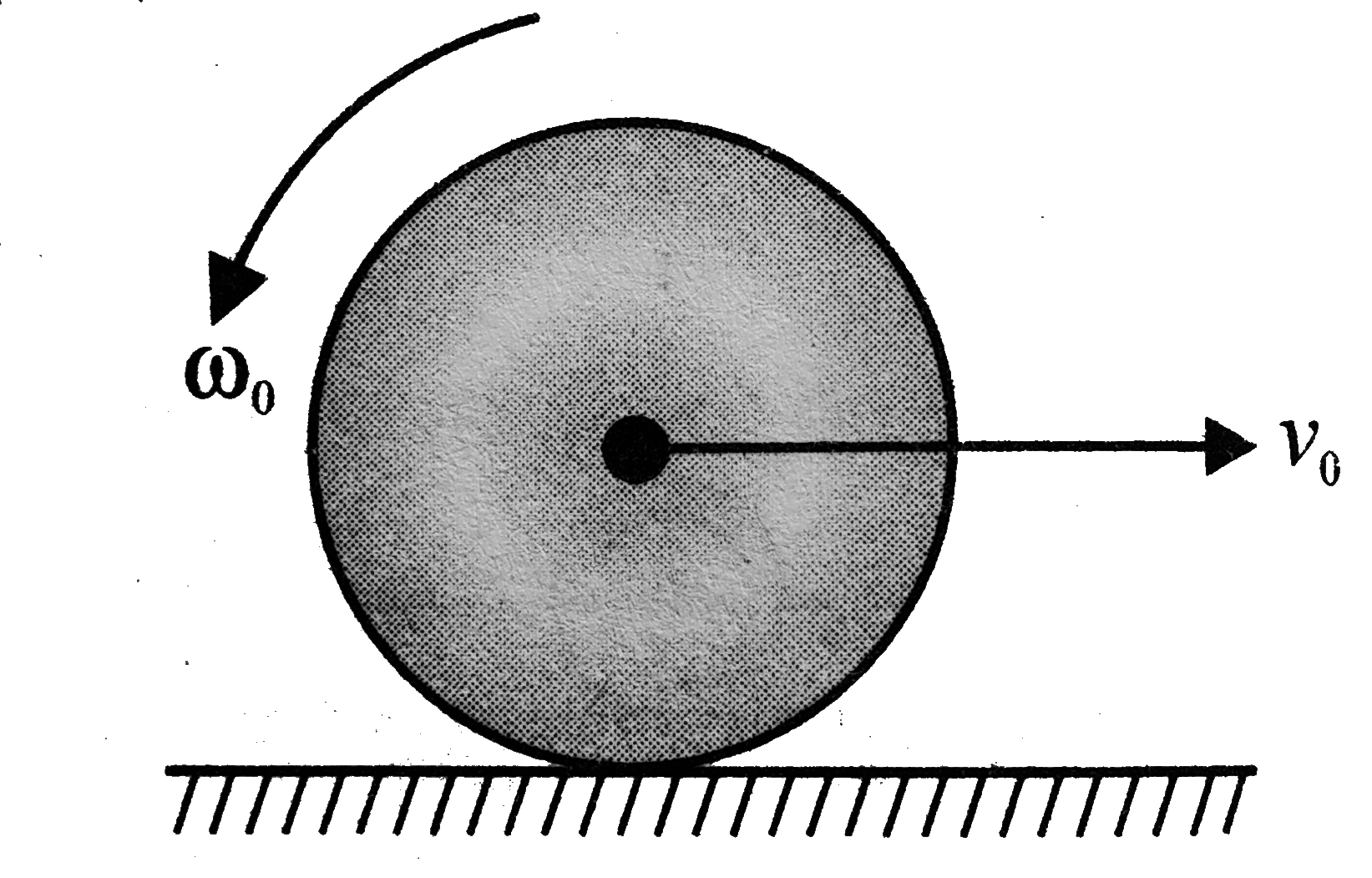 A3v0=2ω0rB2v0=ω0rCv0=ω0rD2v0=3ω0r
A3v0=2ω0rB2v0=ω0rCv0=ω0rD2v0=3ω0rA solid sphere of radius R is placed on a smooth horizontal surface. A horizontal force F is applied at height h from the lowest point. For the maximum acceleration of the centre of mass
Ah=RBh=2RCh=0Dthe acceleration will be same whatever h may be
A rod AB of length 2 m and mass 2 kg is lying on a smooth horizontal x-y plane with its centre at origin O as shown in figure. An impulse J of magnitude 10 N-s is applied perpendicular to AB at A.

The distance of point P from centre of the rod which is at rest just after impact is
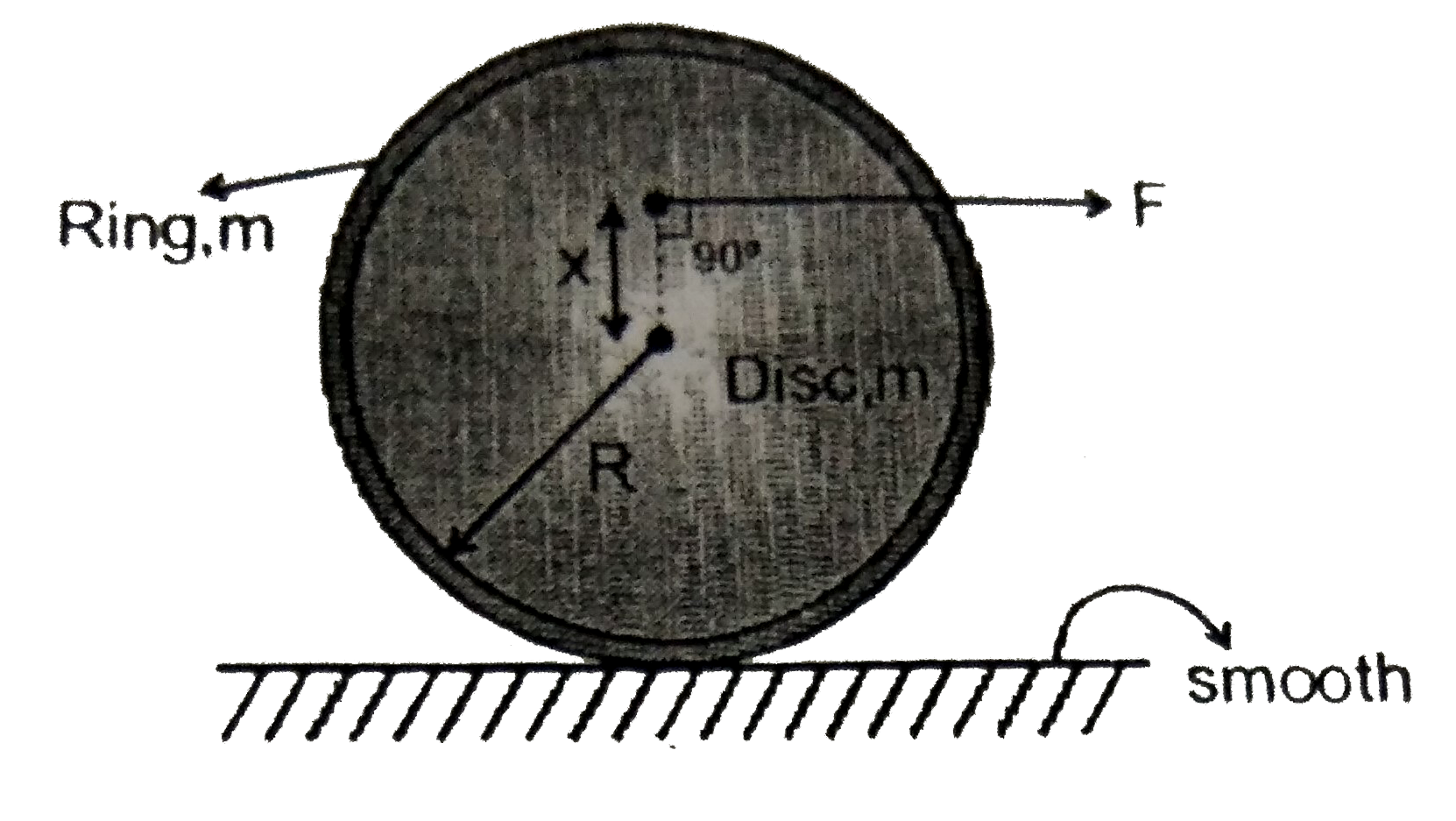
View SolutionA ring and a disc of same mass m and same radius R are joinged concentrically. This system is placed on a smooth plane with the common axis parallel to the plane as shown in figure. A horizontal force F is applied on the system at a point which is at a distance x from the centre. The value of x so that it starts pure rolling is
View SolutionA solid sphere of mass M and radius R is placed on a smooth horizontal surface. It is given a horizontal impulse J at a height h above the centre of mass and sphere starts rolling then, the value of h and speed of centre of mass are –
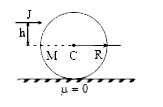
View SolutionA uniform rod of mass m and length l is at rest on smooth horizontal surface. An impulse P is applied to end B as shown.
The point about which rod rotates just after impulse being applied is located at
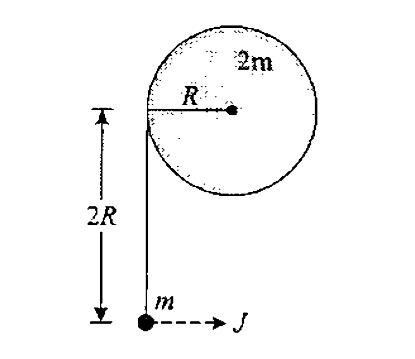
View SolutionA uniform circular disc of mass 2 m and radius R placed freely on a horizontal smooth surface as shown in the figure- 5.116.A particle of mass m is connected to the circumference of the disc with a massless string. Now an impulse J is applied on the particle in the directions shown by dotted line. The acceleration of centre of mass of the disc just after application of implues is (If J =10N−sec.,m=√10kgandR=25cm)
View Solution
