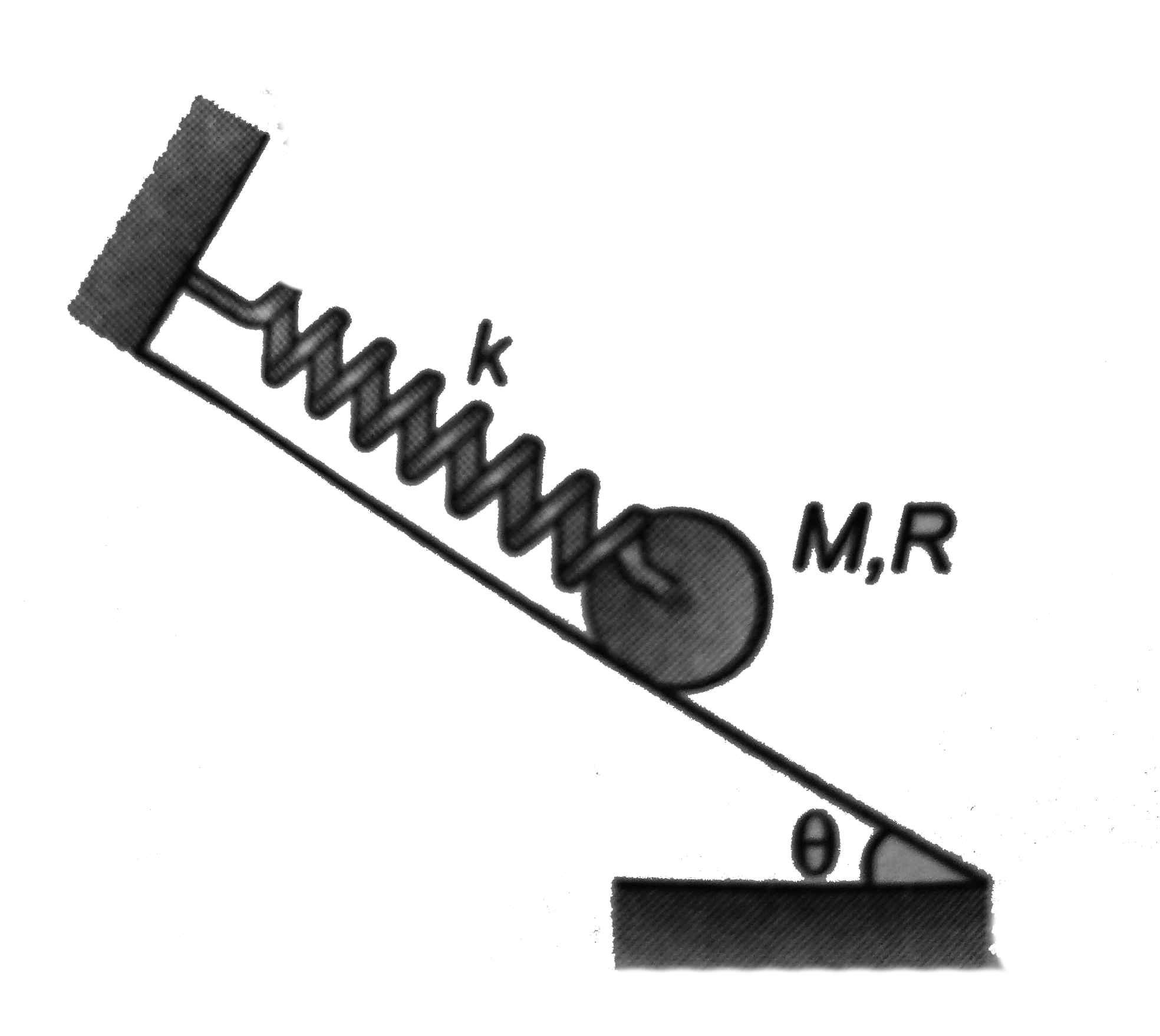
A uniform cylinder of mass $M$ and radius $R$ is released from rest on a rough inclined surface of inclination $θ$ with the horizontal as shown in figure. As the cylinder rolls down the inclined surface, the maximum elongation it the spring stiffness $k$ is

A

$\frac{3}{4} \frac{M g sin θ}{k}$

B

$\frac{2 M g sin θ}{k}$

C

$\frac{M g sin θ}{k}$

D

none of these

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

From energy conservation principle, maximum spring potential energy.
$=$ maximum decrease in gravitational potential energy
$∴ \frac{1}{2} k x_{m}^{2} = M g h = M g (x_{m} sin θ)$
$∴ x_{m} = \frac{2 M g sin θ}{k}$

|

Updated on:21/07/2023

Class 11 PHYSICS RIGID BODY DYNAMICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One or More
A solid cylinder is rolling down a rough inclined plane of inclination $θ$ . Then
AThe friction force is dissipative
BThe friction force is necessarily changing
CThe friction force will aid rotation but hinder translation
DThe friction force is reduced if $θ$ is reduced
Question 2 - Select One or More
A solid cylinder of mass $m$ and radius $r$ is rolling on a rough inclined plane of inclination $θ$ . The coefficient of friction between the cylinder and incline is $μ$ . Then.
Africtional force is always $μ m g cos θ$
Bfriction is a dissipative force
Cby decreasing $θ$ , frictional force decreases
Dfrictiona opposes translation and supports rotation.
Question 3 - Select One
A solid cylinder of mass M and radius R rolls from rest down a plane inclined at an angle $θ$ to the horizontal. The velocity of the centre of mass of the cylinder after it has rolled down a distance d is :
A $\sqrt{\frac{2}{3} g d tan θ}$
B $\sqrt{g d tan θ}$
C $\sqrt{\frac{3}{4} g d sin θ}$
D $\sqrt{\frac{4}{3} g d sin θ}$

DC PANDEY-ROTATIONAL MECHANICS-Level 2 Single Correct

Home
Ask Doubt
Profile