A disc having radius r=2m is placed on smooth horizontal surface. Velocity of point A and B is given as shown in fig. Distance between point O and axis of rotation at the particular instant is
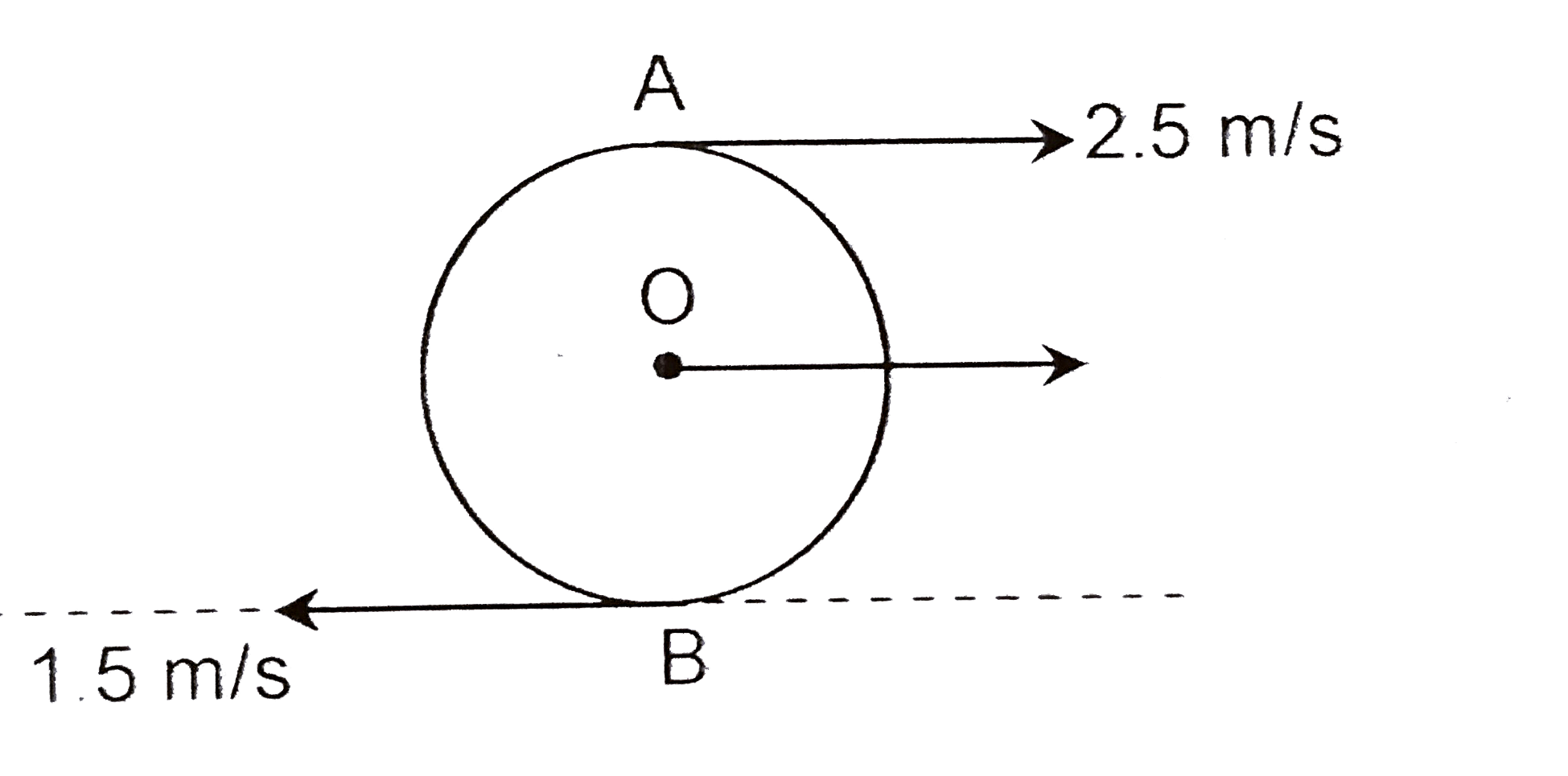
1m
0.5m
0.25m
2m
The correct Answer is:B
2.52+y=1.52−y
∴Y=0.5m

Topper's Solved these Questions
- TEST PAPERSBook:FIITJEEChapter:TEST PAPERSExercise:PHYSICS
Explore 747 Videos
- SIMPLE HARMONIC MOTIONBook:FIITJEEChapter:SIMPLE HARMONIC MOTIONExercise:Assignment Problems (Objective) (Level-II)
Explore 20 Videos
- WORK, ENERGY AND POWER Book:FIITJEEChapter:WORK, ENERGY AND POWER Exercise:COMPREHENSIONS ( Comprehension-II)
Explore 5 Videos
Similar Questions
A disc of radius R is moving on a rough horizontal surface with velocity v and angular speed ω at an instant as shown in figure. Choose the correct statement.

View SolutionA uniform disc of mass m, radius R is placed on a smooth horizontal surface. If we apply a horizontal force F at P as shown in the figure. If F=4N,m=.1kg,R=1m and r=12m then, find the:
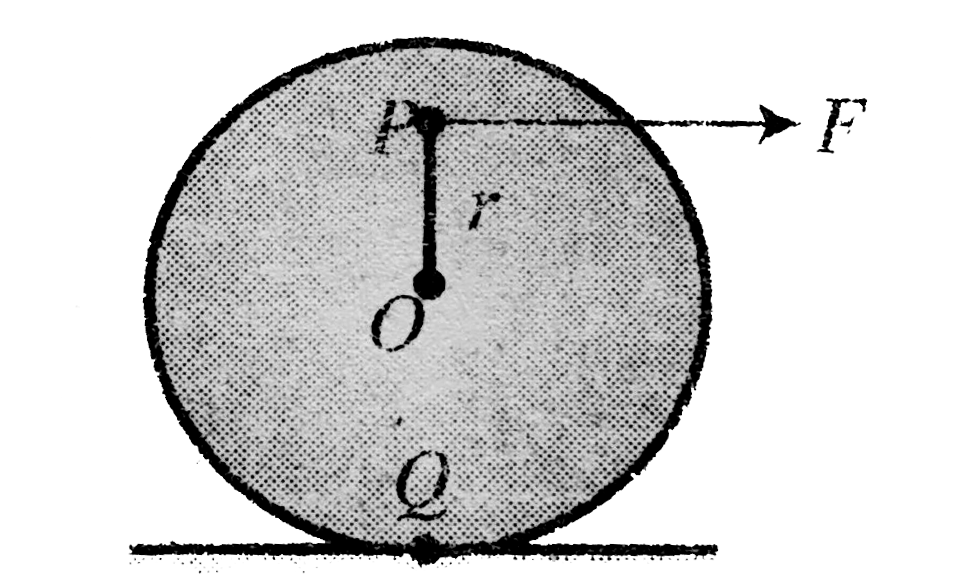
angular acceleration of the disc. (rads−1)
View Solution
Knowledge Check

A uniform circular disc of radius R is placed on a smooth horizontal surface with its plane horizontal and hinged at circumference through point O as shown . An impulse P is applied at a perpendicular distance h from its centre C. The value of h so that the impulse due to hinge is zero, isARBR/2CR/3DR/4A disc of radius R rolls without slipping at speed v along positive x-axis. Velocity of point P at the instant shown in Fig. is
 A→VP=(v+vrsinθR)ˆi+vrcosθRˆjB→VP=(v+vrsinθR)ˆi−vrcosθRˆjC→VP=vrsinθRˆi+vrcosθRˆjD→VP=vrsiθRˆi−vrcosθRˆj
A→VP=(v+vrsinθR)ˆi+vrcosθRˆjB→VP=(v+vrsinθR)ˆi−vrcosθRˆjC→VP=vrsinθRˆi+vrcosθRˆjD→VP=vrsiθRˆi−vrcosθRˆjA disc of radius R rolls on a rough horizontal surface. The distance covered by the point A in one revolution is
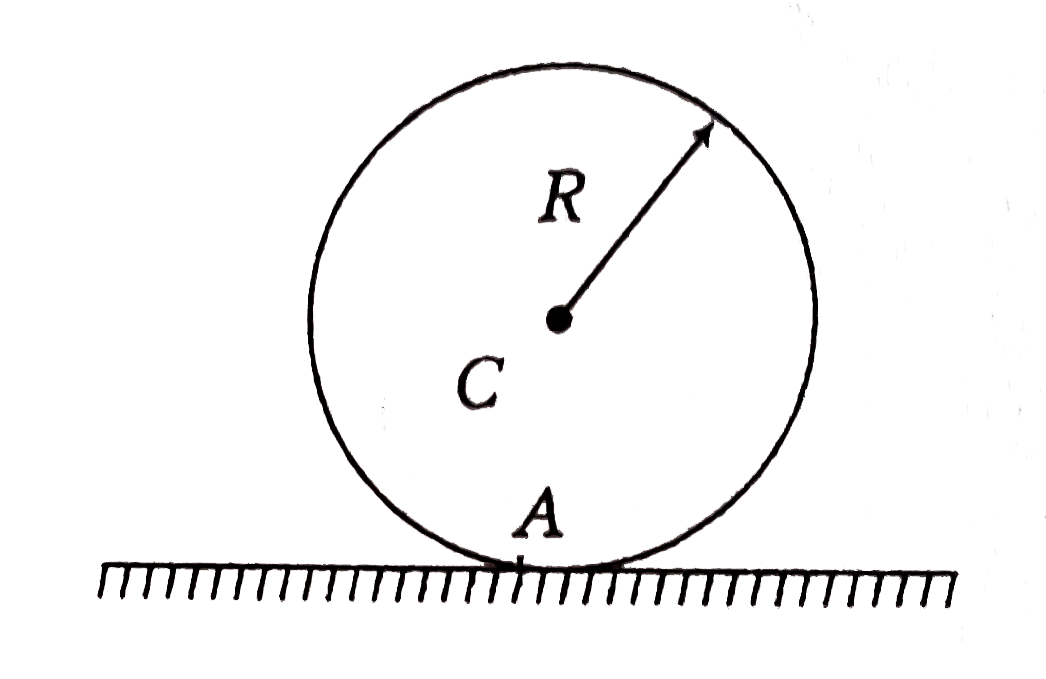 A2πRB2RC8RDπR
A2πRB2RC8RDπR
A uniform disc of mass m, radius R is placed on a smooth horizontal surface. If we apply a horizontal force F at P as shown in the figure. If F=4N,m=.1kg,R=1m and r=12m then, find the:

acceleration of the CM (in ms2)
View SolutionA smooth disc of mass M and radius L√3 is placed at rest horizontally on a smooth horizontal surface. A massless pin is fixed at point P at a distance L/2 from centre O of the disc as shown in the figure. Now a thin uniform rod of mass M and length L is placed horizontally on the surface of the disc parallel to the line OP such that its mid point and centre O of the disc just coincide as shown in figure. Now rod has given angular velocity ω0=24rad/sec in counter clockwies direction as shown. As a result, the end of the rod strikes the pin P and stricks to it rigidly. Calculate the angular velocity of disc just after collision.

View SolutionThe velocity of point A on the rod is 2ms−1 (leftwards) at the instant shown in fig. The velocity of the point B on the rod at this instant is

View SolutionA disc of radius R is rolling purely on a flat horizontal surface, with a constant angular velocity. The angle between the velocity and acceleration vectors of point P is
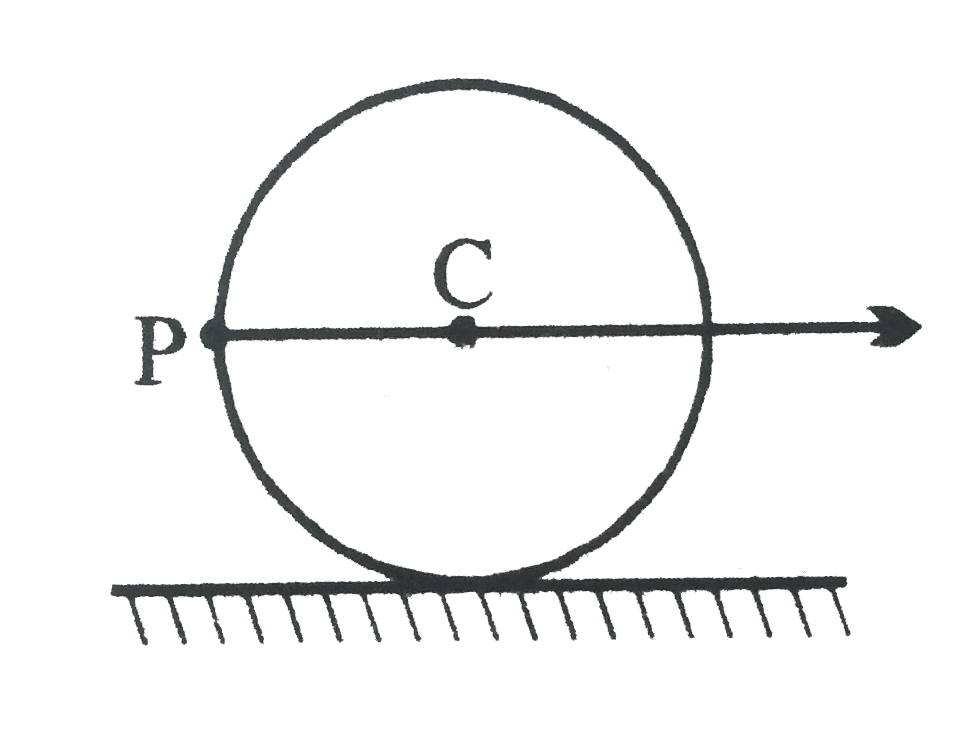 .
.
View Solution
A disc of radius R is rolling purely on a flat horizontal surface, with a constant angular velocity the angle between the velocity ad acceleration vectors of point P is
View Solution

