A man A moves due to East with velocity $6 m s^{- 1}$ and another man B moves in $N - 30^{\circ} E$ with $6 m s^{- 1}$ . Find the velocity of B w.r.t. A.

Video Solution

Text Solution

Verified by Experts

Given, $v_{A} = 6 ˆ i$ ,

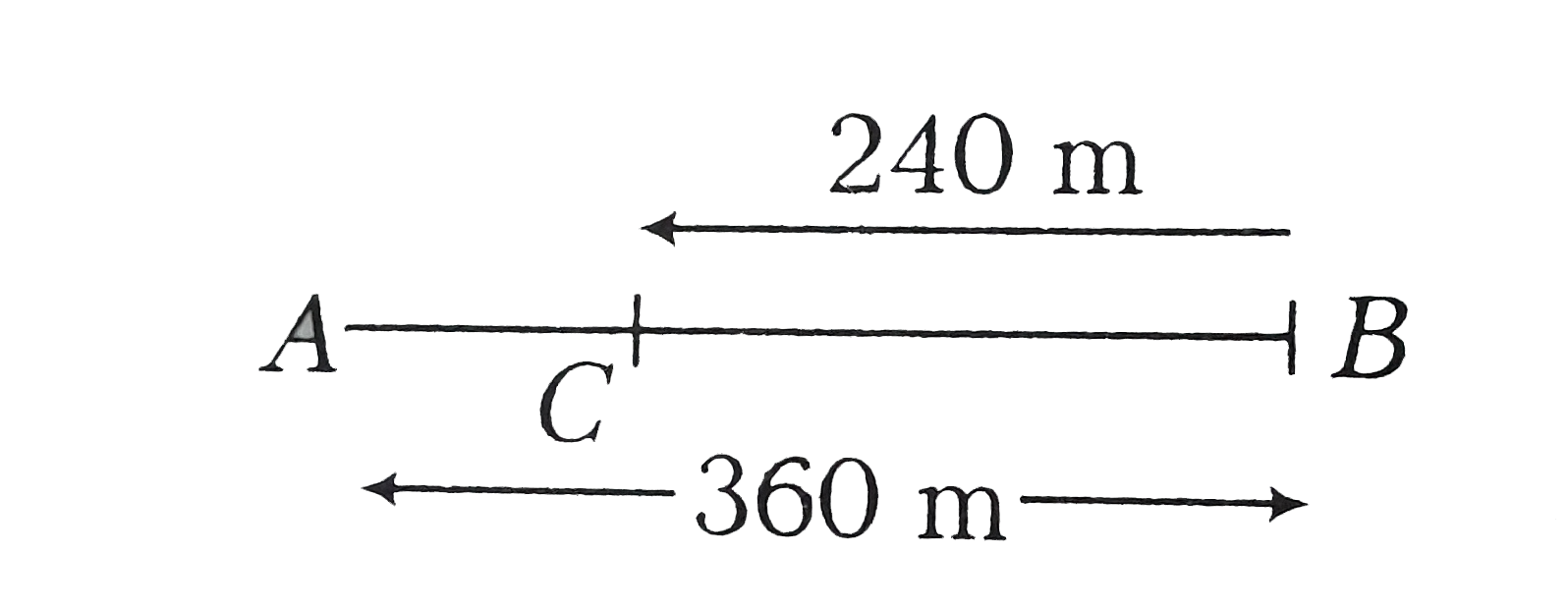
$v_{B} = v_{B} {cos 60}^{\circ} ˆ i + v_{B} {sin 60}^{\circ} ˆ j$
$= 6 (\frac{1}{2}) ˆ i + 6 (\frac{\sqrt{3}}{2}) ˆ j = 3 ˆ i + 3 \sqrt{3} ˆ j$
To find the velocity,
$v_{B A} = v_{B} - v_{A} = (3 ˆ i + 3 \sqrt{3} ˆ j) - 6 ˆ i = - 3 ˆ i + 3 \sqrt{3} ˆ j$
$| v_{B A} | = \sqrt{{(- 3)}^{2} + {(3 \sqrt{3})}^{2}}$
$= \sqrt{9 + 27} = \sqrt{36} = 6 m s^{- 1}$
Here , $ˆ i$ is -ve and $ˆ j$ is +ve. So, second quadrant is possible. Direction,
$tan α = \frac{coefficient of ˆ j}{coefficient of ˆ i} = \frac{3 \sqrt{3}}{- 3} = - \sqrt{3} \Rightarrow α = 60^{\circ}$

|

Updated on:21/07/2023

Class 11 PHYSICS PROJECTILE MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A car A moves along north with velocity 30 km/h and another car B moves along east with velocity 40 km/h. The relative velocity of A with respect to B is
A50 km/h North - East
B50 km/h North-West
C50 km/h at angle ${tan}^{- 1} (3 / 4)$ North of West
D50 km/h at angle ${tan}^{- 1} (3 / 4)$ West of North
Question 2 - Select One
In the figure it is shown that the velocity of lift is $2 m s^{- 1}$ while string is winding on the motor shaft with velocity $2 m s^{- 1}$ and shaft $A$ is moving downward with velocity $2 m s^{- 1}$ with respect to lift , then find out the velocity of block $B$

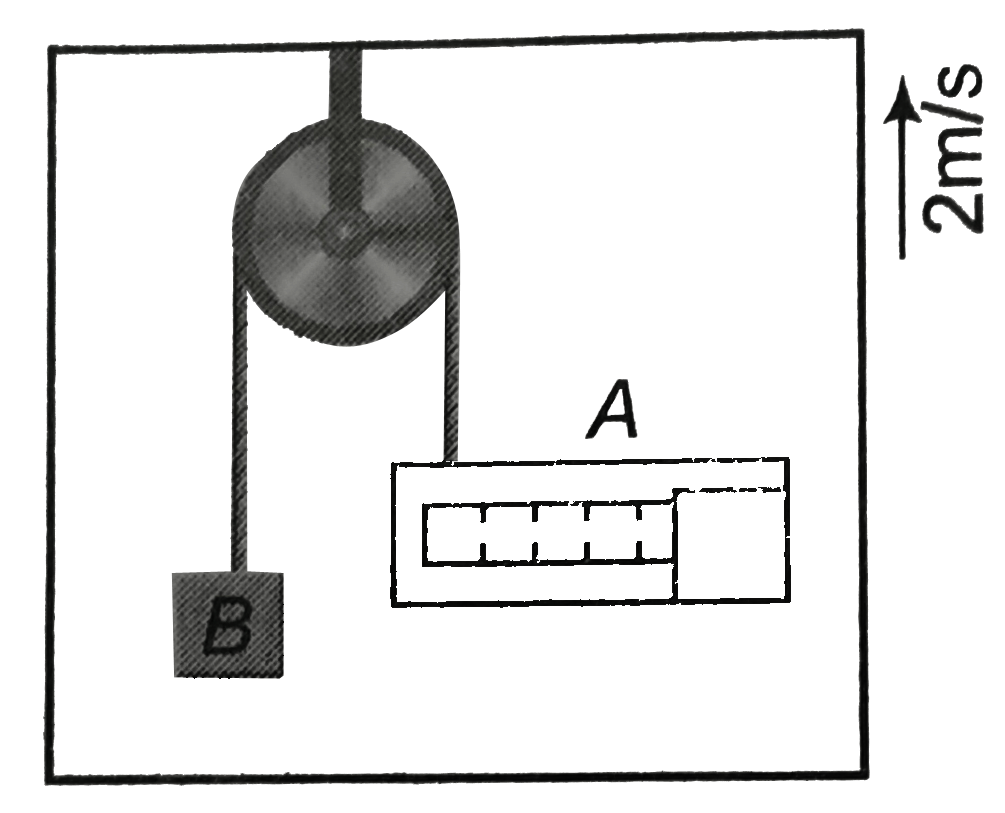A $2 m s^{- 1} ↑ ⏐$
B $2 m s^{- 1} ⏐ ↓$
C $4 m s^{- 1} ⏐ ↓$
D $8 m s^{- 1} ↑ ⏐$
Question 3 - Select One
Out of the two cars A and B car A is moving towards east with velocity of 10 m/s whereas B is moving towards north with a velocity 20 m/s, then velocity of A w.r.t B is ( nearly )
A30 m/s
B10 m/s
C22 m/s
D42 m/s

DC PANDEY-MOTION IN A PLANE-(C )Medical entrances gallery

Home
Ask Doubt
Profile