A thin rod AB of mass M and length L is rotating with angular speed ω0 about vertically axis passing through its ends B on a horizontal smooth table as shown. If at some instant the hinge at end B of rod is opened then which of the following statemtents is / are correct about motion of rod?

the angular speed of the rod after opening the hinge will remain ω0
the angular speed of the rod after opening the hinge will be less then ω0
in the process of opening the hinge the kinetic energy of rod will remain conserved.
angular momentum of rod will remain conserved about centre of mass of rod in the process of opening the hinge
The correct Answer is:A, C, D
Initially ω0 is not changed. After that ω0 decreases because I0ω0=I'ω' initially I0 about B & laterI' is about com.
Then kinetic energy and angular momentum both are conserved due to no external torque.
Topper's Solved these Questions
- SYSTEM OF PARTICLESBook:NARAYNAChapter:SYSTEM OF PARTICLESExercise:Level-VI
Explore 78 Videos
- SYSTEM OF PARTICLESBook:NARAYNAChapter:SYSTEM OF PARTICLESExercise:Level -II(H.W)
Explore 47 Videos
- PHYSICAL WORLDBook:NARAYNAChapter:PHYSICAL WORLDExercise:C.U.Q
Explore 10 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION Book:NARAYNAChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTION Exercise:EXERCISE - IV
Explore 39 Videos
Similar Questions
A uniform rod of mass m and length l0 is rotating with a constant angular speed ω about a vertical axis passing through its point of suspension. Find the moment of inertia of the rod about the axis of rotation if it make an angle θ to the vertical (axis of rotation).
View SolutionA rigid rod of mass m and lengths l, is being rotated in horizontal plane about a vertical axis, passing through one end A. If TA,TBandTC are the tensions in rod at point A, mid point B and point C of rod repsectively, then

View Solution
Knowledge Check
A uniform rod of mass m and length l rotates in a horizontal plane with an angular velocity ω about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is
A12mω2xB12mω2(1−x2l)C12mω2l(1−x2l2)D12mω2l[1−xl]A thin uniform rod of mass m and length L rotates with the constant angular velocity ω about .the vertical axis passing through the rod's suspensjon point O. It describes a carried surface, then:
Acentrifugal force acting on rod is mL2sinθω2 and will pass through centre of massBcentrifugal force acting on rod is mL2sinθω2 and will not pass through centre of massCθ=cos−1(3g2ω2L)Dθ=cos−1(gω2L)A rod AB of mass m and length l is rotating about a vertical axis as shown. It's moment of inertia about this axis is :
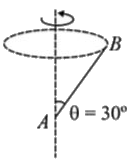 Aml23Bml24Cml216Dml212
Aml23Bml24Cml216Dml212
A rod of mass M and length L lying horizontally is free to rotate about a vertical axis through its end. A horizontal force F on the rod at the other end, the force always remains perpendicular to the rod. Find the angular velocity of the rod when it has turned an angle π/2.
View SolutionA rod of length l is rotating with an angular speed ω about one of its ends which is at a distance a from an infinitely lonf wire carrying current i. Find the emf induced in the rod at the instant shown in .
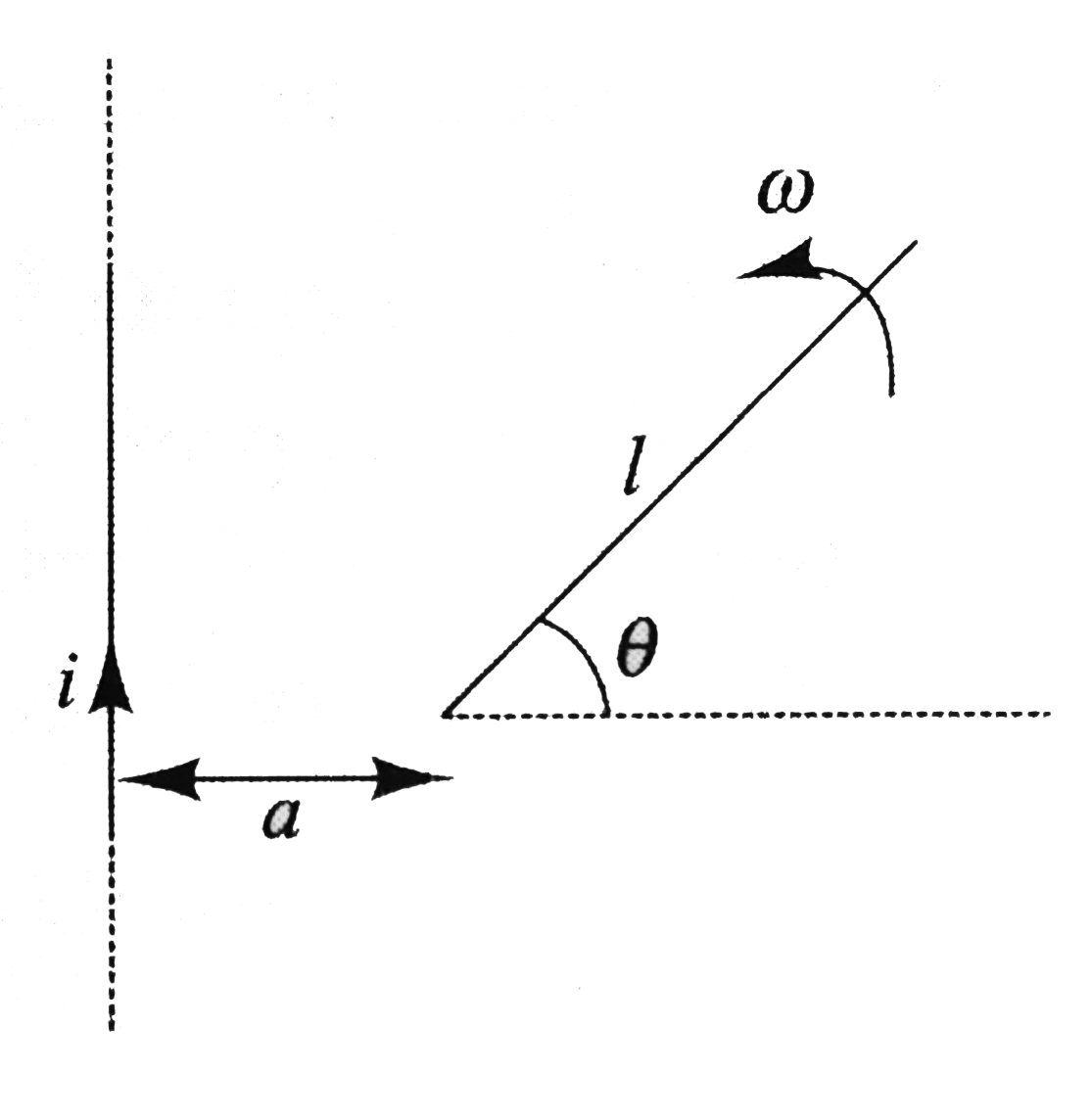
View SolutionA uniform metal rod is rotated in horizontal plane about a vertical axis passing through its end at uniform rate. The tension in the rod is
View SolutionA uniform rod of mass m and length L lies radialy on a disc rotating with angular speed ω in a horizontal plane about vertical axis passing thorugh centre of disc. The rod does not slip on the disc and the centre of the rod is at a distance 2L from the centre of the disc. them the kinetic energy of the rod is

View SolutionA rod of length l is rotated with angular speed ω about an axis passing through the centre of rod and perpendicular to its length. A uniform magnetic field B is applied parallel to the axis of rotation, Potential difference developed between the ends of the rod is
View Solution

