There particles each of mass m can slide on fixed frictioless circular tracks in the same horizontal plane as shown. Particle m1(=m) moves with velocity v0 and hits particle m2(=m), the cofficient of restitution being e=0.5 . Assume that m2 and m3(=m) are at rest initially and lie along a radial line before impact, and the spring is initially unstretched.

Velocity of m2 immediately after impact is
v04
3v04
v02
3v02
The correct Answer is:B
First we apply conservation of momentum on m1 and m2:m1v0=m1v1+m2v2
v0=v1+v2.....(1) As m1=m2 Where v1 and v2 are velocities of m1 and m2 immediately after impact.
From definition of coefficient of restitution.
e=12=−v2−v10−v0 or v0=2(v2−v1)......(2)
On solving eqns. (1) and (2),
We get, v1=v04 and v2=3v04
The spring has maximum extension when angular velocity w of m2 about O is same. Now we apply conservation of angular momentum.
m(34v0)2R=mR2ω+m(2R)2ω or rω=32v05R
velocities of m2=2Rω=35v0
Velocity of m3=Rω=310v0

In order to determine maximum extension in the spring. we apply law of conservation of energy.
12m(34v0)=12mR2(32v05R)+12m(2R)2(32v05R)+12kΔx2max
Omn solving for Δx, we get Δx2max=34v0√m5R
Topper's Solved these Questions
- SYSTEM OF PARTICLESBook:NARAYNAChapter:SYSTEM OF PARTICLESExercise:Level-VI
Explore 78 Videos
- SYSTEM OF PARTICLESBook:NARAYNAChapter:SYSTEM OF PARTICLESExercise:Level -II(H.W)
Explore 47 Videos
- PHYSICAL WORLDBook:NARAYNAChapter:PHYSICAL WORLDExercise:C.U.Q
Explore 10 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION Book:NARAYNAChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTION Exercise:EXERCISE - IV
Explore 39 Videos
Similar Questions
A particle of mass m moving with velocity u collides elastically head on with a particle of mass 2m at rest. After collision the heavier particle moves with velocity?
View SolutionA particle of mass'm' is projected with velocity v0 at an angle 'α' with the horizontal. The coefficient of restitution for any of its impact with the smooth ground is e.

Find total time taken by the particle before it stops moving vertically?
View Solution
Knowledge Check
Three particles each of mass 'm' can slide on fixed frictionless circular track in the same horizontal plane as shown in the figure. Particle m1 moves with velocity v0 and hits particle m2, the coefficient of restitution being θ=1/2. AsSigmae m2 and m3 are initially in rest and lie along a radial line before impact and the spring is initially Unstretched. Then,
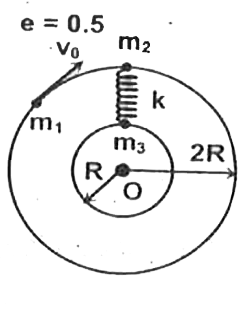
The velocity of m3 when extension in the spring is maximumA110v0B310v0C710v0Dnone of theseThree particles each of mass m can slide on fixed frictionless horizontal circular tracks in the same horizontal plane as shown in the figure. The coefficient of restitution being e=0.5. Assuming that m2 and m3 are at rest initially and lie along a radial line before impact and the string is initially unstretched, then maximum extension in spring in subsequent motion
 A34V0√mkB34V0√m5kC34V0√2m5kD35V0√mk
A34V0√mkB34V0√m5kC34V0√2m5kD35V0√mkA particle moving with velocity (2ˆi−3ˆj) m/s collides with a surface at rest in xz–plane as shown in figure and moves with velocity (2ˆi+2ˆj) m/s after collision. Then coefficient of restitution is :
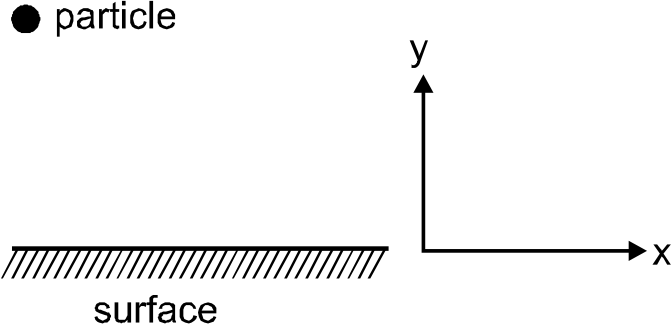 A23B1C√813D45
A23B1C√813D45
A particle of mass m is strikes on ground at an angle of incidence 30∘ with initial speed of 5 m/s . Calculate (i) its velocity after impact (ii) angle of reflection . Given that the coefficient of restitution is 1√3
View SolutionA smooth wedge of mass M is kept at rest on a smooth horizontal surface . Inclined face of the wedge make an angle θ with the horizontal . A particle of mass m collides normal to inclined face of wedge . If speed of the particle just before collision is u and coefficient of restitution is e then find velocity of wedge after collision .
View SolutionA particle of mass m1 collides head on with a stationary particles of mass m2. If m1m2 gte, where e is the coefficient of restitution, then :
View SolutionA particle of mass m moves along line PC with velocity v as shown. What is the angular momentum of the particle about P?
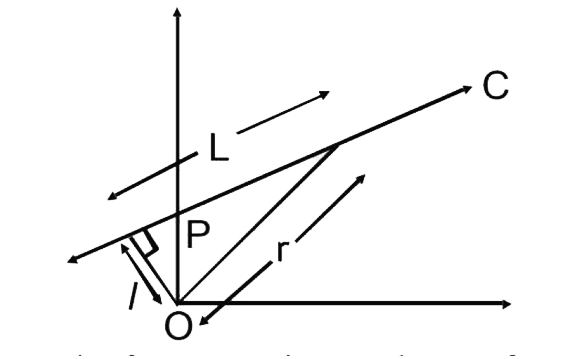
View SolutionA particle of mass m moves along line PC with velocity v as shown. What is the angular momentum of the particle about O?

View Solution

