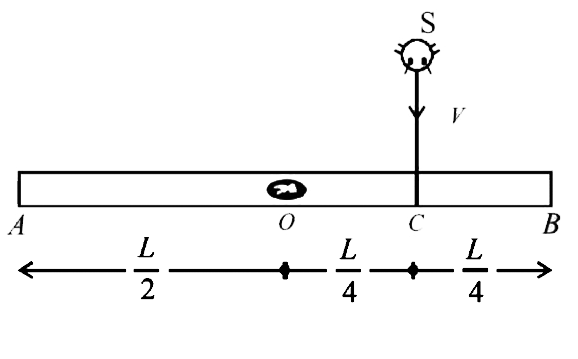
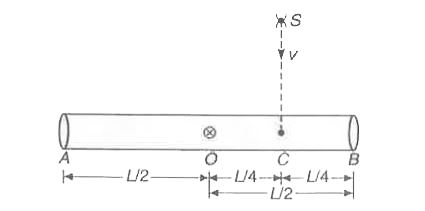
A homogeneous rod AB of length L = 1.8 m and mass M is pivoted at the center O in such a way that it can rotate it can rotate freely position. An insect S of the same mass M falls vertically with speed V on the point C, midway between the points O and B. Immediately after falling, the insect moves towards the end B such that the rod rotates with a constant angular velocity omega.
(a) Determine the angular velocity ω in terms of V and L.
(b) If the insect reaches the end B when the rod has turned through an angle of 90∘, determine V.
37√2gL
712√2gL
112√gL
27√2gL
The correct Answer is:B
A angular momentum of system of rod and insect, just after collision =initial angular momentum of insect about O
∴{ML212+M(L4)2}ω=MυL4
ω=12v7L
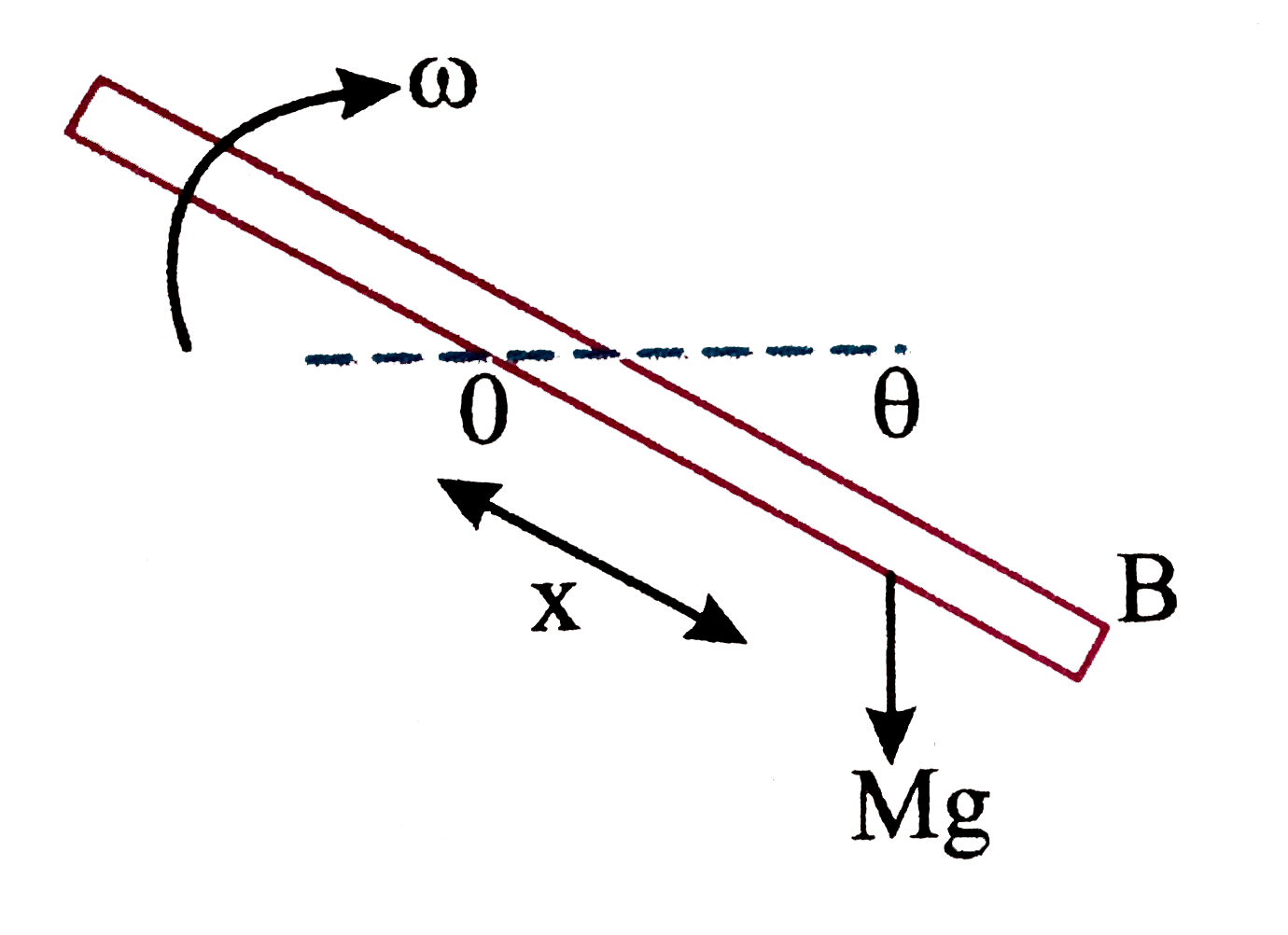
Let the insect fall on the rod at time t=0, then at time t, inclination of rod with horizontal, θ=ωt
∴ Angular momentum
L=Iω=(ML212+Mx2)ω
Torque produced by weight of insect, τ=Mgxcosθ=Mgxcosωt
τ=ddt,LF=μN∴μ=0.2
Topper's Solved these Questions
- SYSTEM OF PARTICLESBook:NARAYNAChapter:SYSTEM OF PARTICLESExercise:Level-VI
Explore 78 Videos
- SYSTEM OF PARTICLESBook:NARAYNAChapter:SYSTEM OF PARTICLESExercise:Level -II(H.W)
Explore 47 Videos
- PHYSICAL WORLDBook:NARAYNAChapter:PHYSICAL WORLDExercise:C.U.Q
Explore 10 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION Book:NARAYNAChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTION Exercise:EXERCISE - IV
Explore 39 Videos
Similar Questions
The point P of a string is pulled up with an acceleration g. Then the acceleration of the hanging disc (w.r.t ground) over which the string is wrapped, is
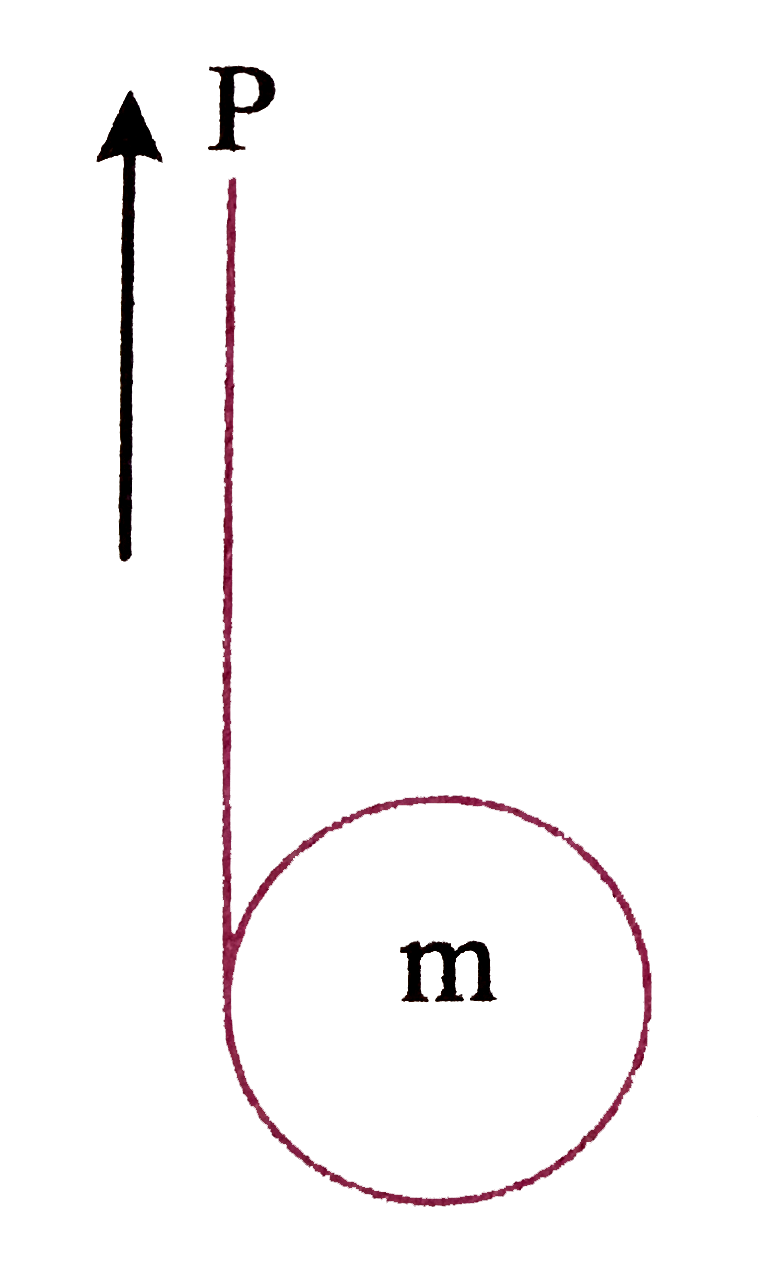
View SolutionFour particles, each of mass 1kg are placed at the corners of a square of side 1m in the XY plane. If the point of intersecting of the diagonals of the square is taken as the origin, the co-ordinates fo the centre of mass are
View SolutionWhat is the discovery of CV Raman?
View SolutionFor which of the following does the centre of mass lie outside the body ?
View SolutionA homogeneous rod AB of length L = 1.8 m and mass M is pivoted at the center O in such a way that it can rotate it can rotate freely position. An insect S of the same mass M falls vertically with speed V on the point C, midway between the points O and B. Immediately after falling, the insect moves towards the end B such that the rod rotates with a constant angular velocity omega.
(a) Determine the angular velocity ω in terms of V and L.
(b) If the insect reaches the end B when the rod has turned through an angle of 90∘, determine V.

View Solution
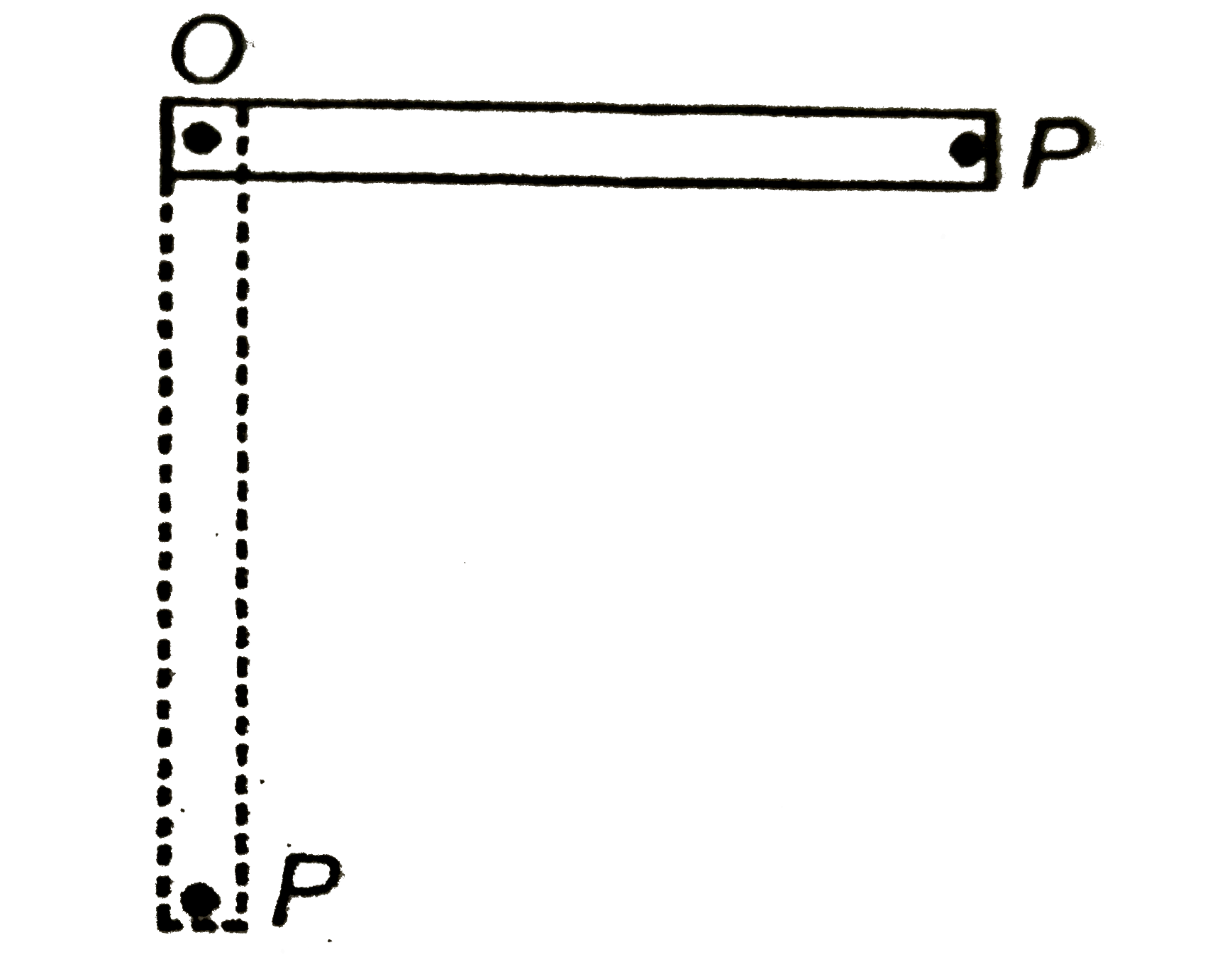
A uniform rod of length L and mass m is free to rotate about a frictionless pivot at one end as shown in figure. The rod is held at rest in the horizontal position and a coin of mass m is placed at the free end. Now the rod is released The reaction on the coin immediately after the rod starts falling is
View SolutionConsider a rod of mass M and length L pivoted at its centre is free to rotate in a vertical position plane. The rod is at rest in the vertical position. A bullet of mass M moving horizontally at a speed v strikes and embedded in one end of the rod. The angular velocity of the rod just after the collision will be.
View SolutionA uniform rod AB of mass m and length 2a is falling freely without rotationb under gravity with AB horizontal. Suddenly the end A is fixed when the speed of the rod is v. The angular speed which the rod begains to rotate is
View SolutionA rod AB of mass m and length L is rotating in horizontal plane about one of its ends which is pivoted. The constant angular speed with which the rod is rotating is omega . The force applied on the rod by the pivot is
View SolutionA rod of mass m and length L is pivoted at the bottommost point O and can freely rotate about the point O . The rod is disturbed from the vertical position so that it starts rotating about O . When it makes an angle theta with the vertical
View SolutionA rod of mass m and length L is pivoted at a point O and kept in horizontal position as shown in figure. Now it is released from this position so that it can rotates freely about the point O in downward direction. When it becomes vertical
View Solutionलम्बाई L=1.8 मी तथा द्रव्यमान M किग्रा की एक समांग छड़ AB अपने केंद्र O पर इस प्रकार कीलकित है कि यह ऊर्ध्वाधर तल में चित्रानुसार स्वतंत्र रूप से घूम सकती है। आरंभ में छड़ क्षैतिज अवस्था में है। उसी द्रव्यमान M का एक कीड़ा S, बिंदुओं O व B के बीच C पर वेग v से ऊर्ध्वाधर गिरता है। गिरने के तुरंत बाद कीड़ा सिरे B की ओर इस प्रकार रेंगता है कि छड़ नियत कोणीय वेग ω से घूमती है।
a. कोणीय वेग ω का मान v तथा L के पदों में ज्ञात कीजिए।
b. यदि कीड़े के B पर पहुंचने पर छड़ 90∘C घूम जाती है तो v का मान ज्ञात कीजिए।
View Solutionएक समरूप छड़ AB की लम्बाई l तथा द्र्वयमान m है , यह बिंदु A के परित घूर्णन के लिए स्वतंत्र है । क्षैतिज स्थिति में विराम से छड़ को छोड़ा जाता है । छड़ का A के परित : जड़त्व आघूर्ण ml23 हो तब का प्रारम्भिक कोणीय त्वरण होता -

View SolutionA rod of mass m,length l pivoted at its centre is free to rotate in a vertical plane.The rod is at rest and is in vertical position.A bullet of mass m/2 moving horizontally with speed v strikes and sticks to one end of the rod. Angular velocity of system just after collision is
View SolutionA homogeneous rod of length L=1.8 m and mass M is pivoted at the centre O in such a way that it can rotate freely in the vertical plane as shown fig. The rod is initially in the horizontal position. An insect S of the same mass M falls vertically with speed V on the point C, midway between the point O & B. Immediately after falling the insect moves towards the end B such that the rod rotates with constant angular velocity ω

View SolutionA homogeneous rod XY of length 'L' and mass 'M' pivoted at the centre C such that it can rotate freely in vertical plane. Initially the rod is in the horizontal position .A blob of wax of same mass M as that of the rod falls vertically with the speed 'V' and the sticks to the rod midway between points 'C' and 'Y'. If the rod rotates with angular speed ω what will be angular speed in terms of V and L?
View Solution