A thin uniform rigid rod of mass m and length l is in mechanical equilibrium under the constraints of horizontal and vertical rough surfaces. Then select correct option(s):

the net torque of normal reaction about O is equal to mgl2cosθ
the net torque due to friction about O is zero
the net torque due to normal reaction is numerically equal to the net torque due to the frictional force about the CM of the rod
all of the above
The correct Answer is:A, B, C, D
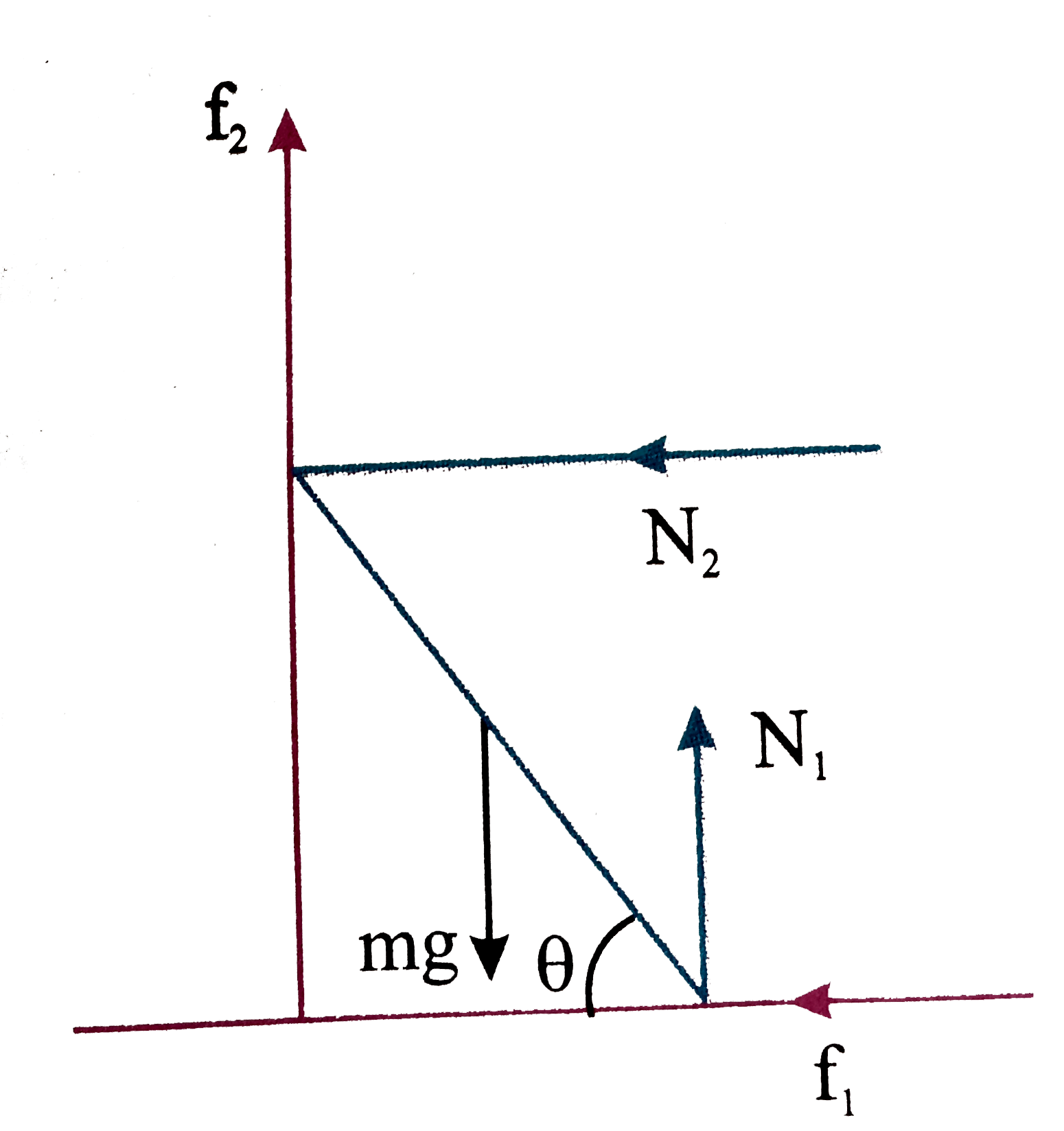
N1=mg−f2.....(1),N2=f1.....(2)
Now taking moment about A
N2×lsinθ+f2×lcosθ=mgl2×cosθ......(3)
Take moment about point B
N1×Icosθ=mg×l2cosθ+f1×lsinθ....(4)
τ0(of normals)=
N1lcosθ+N2×lsinθ=mg2
lcosθ+mg2cotθ=2mglcosθ/2
B,C&Dare easily explain
Topper's Solved these Questions
- SYSTEM OF PARTICLESBook:NARAYNAChapter:SYSTEM OF PARTICLESExercise:Level-VI
Explore 78 Videos
- SYSTEM OF PARTICLESBook:NARAYNAChapter:SYSTEM OF PARTICLESExercise:Level -II(H.W)
Explore 47 Videos
- PHYSICAL WORLDBook:NARAYNAChapter:PHYSICAL WORLDExercise:C.U.Q
Explore 10 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION Book:NARAYNAChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTION Exercise:EXERCISE - IV
Explore 39 Videos
Similar Questions
Find the M.I. of thin uniform rod of mass M and length L about the axis as shown.

View SolutionA uniform rod of mass M and length L is standing vertically along the y-axis on a smooth horizontal surface as shown. A small disturbance causes the lower end to slip on the smooth horizontal surface and rod starts falling. The path followed by centre of mass of the rod during the fall is

View Solution
Knowledge Check
A thin uniform rigid rod of length l is hinged at one end so that it can move ina vertical plane by rotating about a horizontal axis through upper end. The lower end is given a sharp blow and made to acquire a linear velocity Maximum height attained by lower end of the rod is:
 Av203g for v0<√6glB3v20g for v0<√6glC2l for v0≥√6glDl for v0=√3gl
Av203g for v0<√6glB3v20g for v0<√6glC2l for v0≥√6glDl for v0=√3glA thin uniform vertical rod of mass m and length l pivoted at point O is shown in Fig. The combined stiffness of the springs is equal to k. The mass of the springs is negligible. The angular frequency of small oscillation is
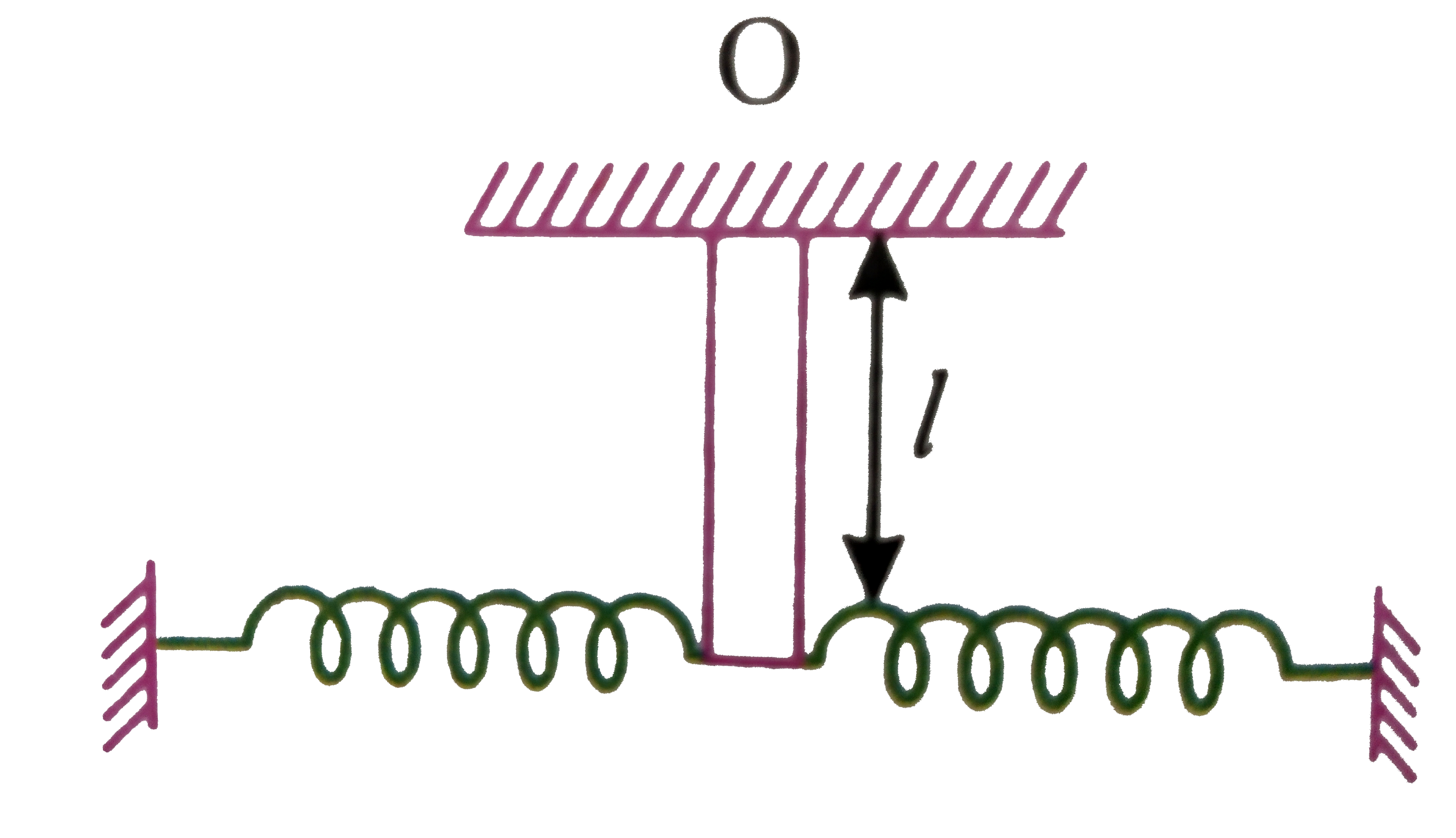 A√3k2m+glB√3k2m+3glC√3km+3g2lD√3km+2g3l
A√3k2m+glB√3k2m+3glC√3km+3g2lD√3km+2g3l
A thin uniform vertical rod of mass m and length l pivoted at point O is shown is Fig. The combined stiffness of the springs is equal to k. The mass of the spring is negligible. The frequency of small oscillation is .A√3k2m+glB√3k2m+3glC√3km+3g2lD√3km+2g3l
Find the frequency of small oscillatinos of a thin uniform vertical rod of mass m and length l hinged at the point O (figure). The combined stiffness fo the springs is equal to x. The mass of the springs is negligible.
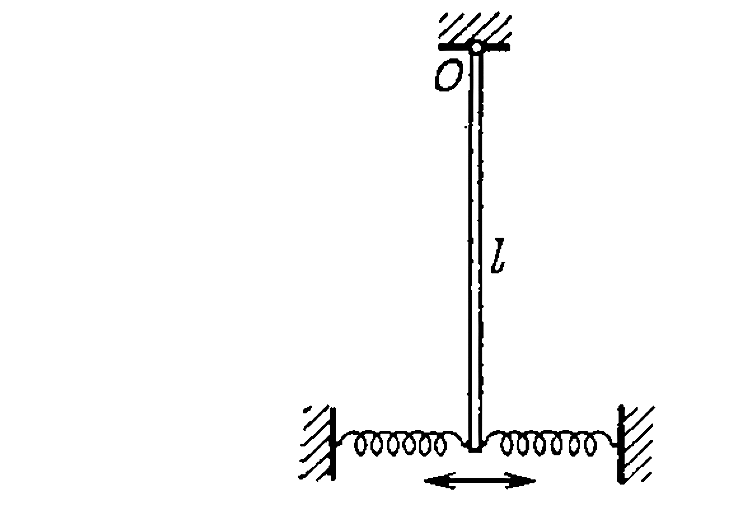
View SolutionA uniform stick of mass M and length L is kept vertical on a frictionless horizontal floor. If the stick is allowed to fall, then mark the correct alternatives
View SolutionA uniform thin rod of mass m and length l is standing on a smooth horizontal surface. A slight disturbance causes the lower end to slip on the smooth surface and the rod starts falling. Find the velocity of centre of mass of the rod at the instant when it makes an angle θ with horizontal.
View SolutionA thin uniform rod of mass m and length L rotates with the constant angular velocity ω about .the vertical axis passing through the rod's suspensjon point O. It describes a carried surface, then:
View SolutionA thin uniform rod of mass m and length l is kept on a smooth horizontal surface such that it can move freely. At what distance from centre of rod should a particle of mass m strike on the rod such that the point P at a distance l3 from the end of the rod is instantaneously at rest just after the elastic collision?
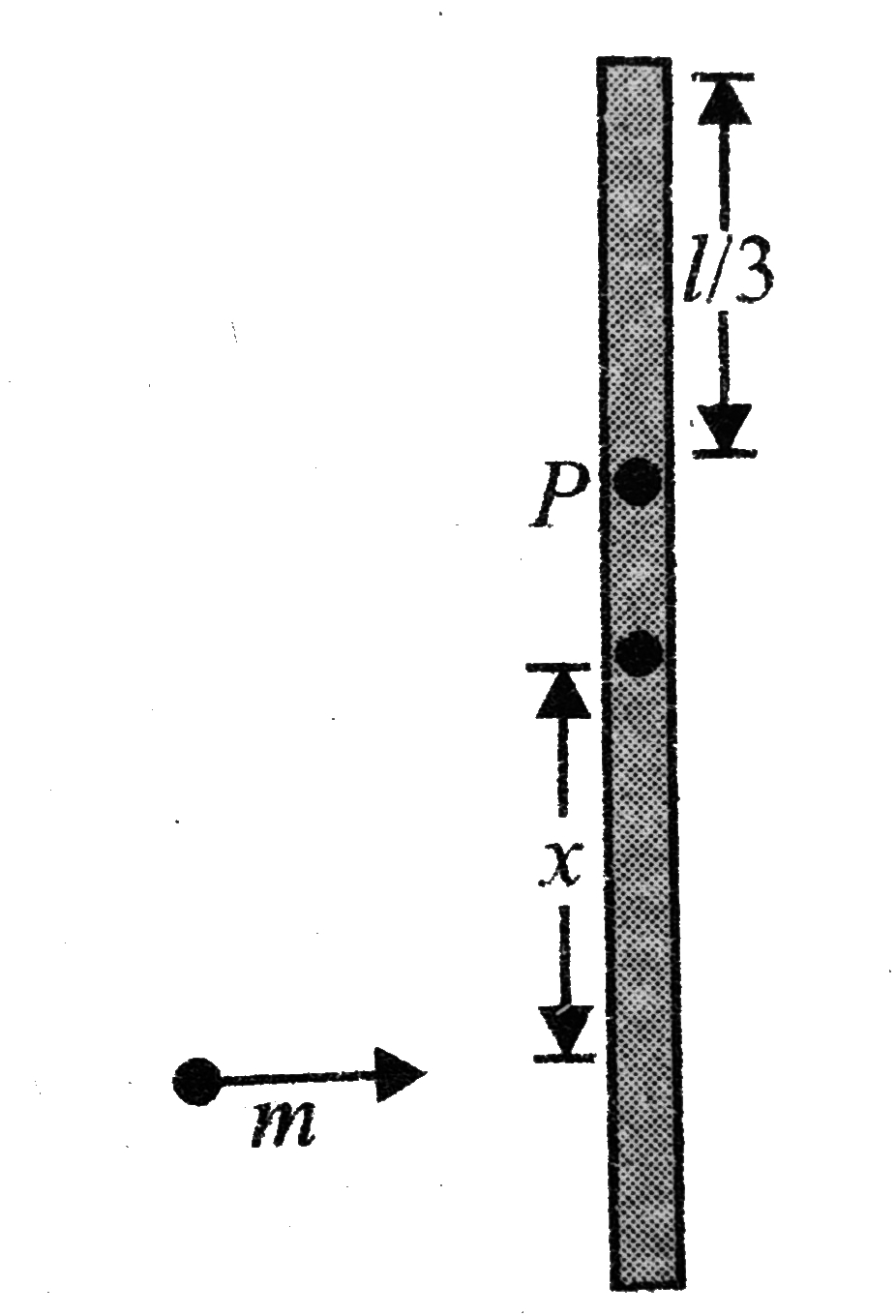
View Solution
