A man of mass 100kg stands at the rim of a turtable of radius 2m and moment of inertia 4000kgm2 mounted on a vertical frictionless shaft at its centre. The whole system is initially at rest. The man now walks along the outer edge of the turntable with a velocity of 1m/s relative to the earth
a. With what angular velocity and in what direction does the turntable rotate?
b. Through what angle will it have rotated when the man reaches his initial position on the turntable?
c. Through what angle will it have rotated when the man reaches his initial position relative to the earth?
π11rad/sec
3π11rad/sec
2π11rad/sec
4π11rad/sec
The correct Answer is:A
If the man complete one revolution relative to the table then θmt=2π,2π=θm−θt
2π=ωmt−ωtt(where t is time taken)
t=2π/(ωm−ωt)=2π(0.5+0.05)
Angular displacement of table is
θt=ωtt=−5.05×(2π/0.55)=−2π11radian
Topper's Solved these Questions
- SYSTEM OF PARTICLESBook:NARAYNAChapter:SYSTEM OF PARTICLESExercise:Level-VI
Explore 78 Videos
- SYSTEM OF PARTICLESBook:NARAYNAChapter:SYSTEM OF PARTICLESExercise:Level -II(H.W)
Explore 47 Videos
- PHYSICAL WORLDBook:NARAYNAChapter:PHYSICAL WORLDExercise:C.U.Q
Explore 10 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION Book:NARAYNAChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTION Exercise:EXERCISE - IV
Explore 39 Videos
Similar Questions
A man of mass m stands on a horizontal platform in the shape of a disc of mass m and radius R, pivoted on a vertical axis through its centre about which it can freely rotate. The man starts to move around the centre of the disc in a circle of radius r with a velocity v relative to the disc. Calculate the angular velocity of the disc.
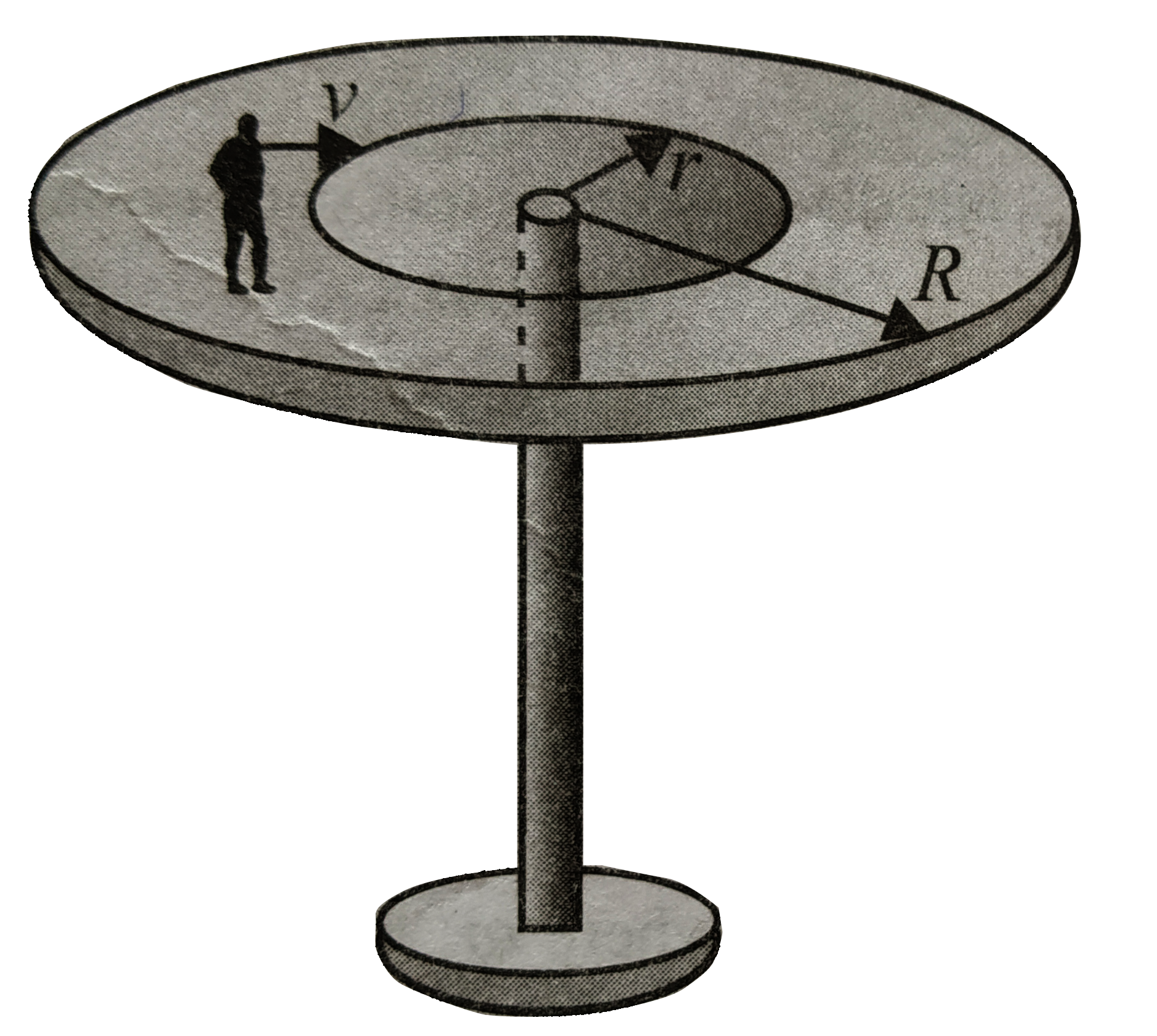
View Solutionwhat is the momentum of a man of mass 75kg when he walks with a velocity of 2m/s?
View Solution
Knowledge Check
A circular platform is mounted on a vertical frictionless axle. Its radius is r=2m and its moment of inertia is I=200kg−m2. It is initially at rest. A 70kg man stands on the edge at speed v0=1.0m/s relative to the ground. The angular velocity of the platform is:
A1.2rad/sB0.4rad/sC2.0rad/sD0.7rad/sA circular platform is mounted on a vertical frictionless axle. Its radius is r=2m and its moment of inertiaI=200kgm2. It is initially at rest. A 70kg man stands on the edge of the platform and begins to walk along the edge at speed v0=1ms−1 relative to the ground. The angular velocity of the platform is.
A1.2rads−1B0.4rads−1C0.7rads−1D2rads−1A man stands at the centre of turn table and the turn table is rotating with certain angular velocity. If he walks towards rim of the turn table, then
Amoment of inertia of the system decreasesBangular momentum of system increasesCangular velocity of the system increasesDkinetic energy of the system decreases
If a constant torque of 500 Nm turns a wheel of moment of inertia 100kgm2 about an axis through its centre, find the gain in angular velocity in 2s.
View SolutionA person of mass m stands at the edge of a circular platform of radius R and moment of inertia. A platform is at rest initially. But the platform rotate when the person jumps off from the platform tangentially with velocity u with respect to platfrom. Determine the angular velocity of the platform.
View SolutionSuppose a person of mass m stands at the edge of a circular platform of radius R and moment of inertia I. The platform is at rest initially, but the platform begins to rotate when the person begins to move with velocity v. Determine the angular velocity of the platform.
View SolutionA 60.0−kg woman stands at the western rim of a horizontal turntable having a moment of inertia of 50kg.m2 and radius of 2.0m. The turntable is initially at rest and free to rotate abot a frictionless, vertical axle through its centre. The woman then starts walking around the rim clockwise(as viewed from above the system) at constant speed of 1.50m/s relative to the Earth. The final angular velocity of the woman and the turntable systems.
View SolutionA disc of moment of inertia 2kgm2 is acted upon by a constant torque of 40 Nm. If it is initially at rest, then the time taken by it to acquire an angular velocity 100 rad/s will be
View Solution

