A string is wrapped several time on a cylinder of mass M and radius R, the cylinder is pivoted about its axis of symmetery . A block mass of m tied to the string rests on support so that the string is black. The block is lifted upto a height h and the support is removed. (shown in figure)
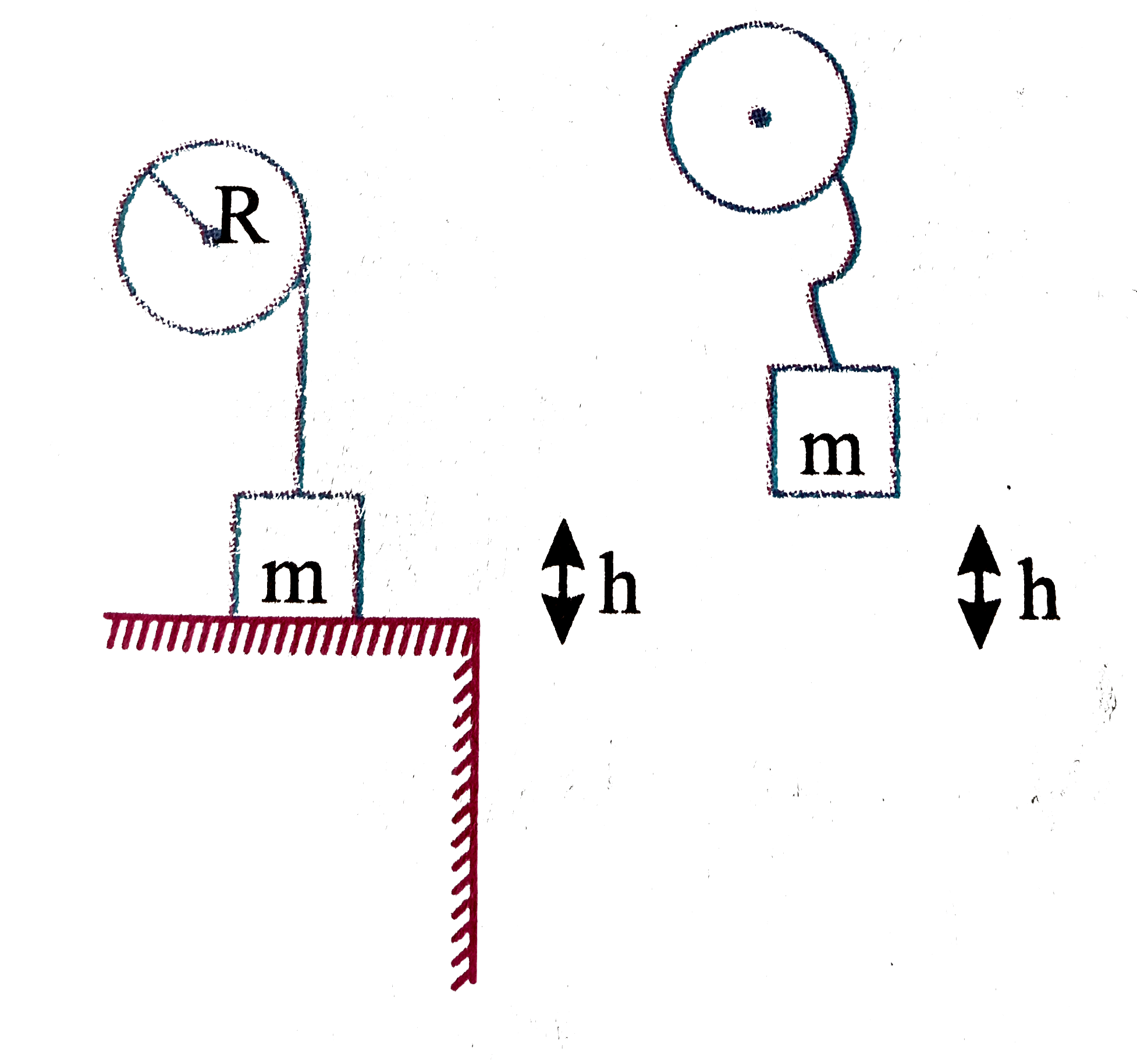
If M=m, what friction of KE is lost due to the jerk developed in the string
1/2
2/3
1/3
1/4
The correct Answer is:C
For M=m,K1=2K03 so the fraction lost is (K0−K1K0)=13
Topper's Solved these Questions
- SYSTEM OF PARTICLESBook:NARAYNAChapter:SYSTEM OF PARTICLESExercise:Level-VI
Explore 78 Videos
- SYSTEM OF PARTICLESBook:NARAYNAChapter:SYSTEM OF PARTICLESExercise:Level -II(H.W)
Explore 47 Videos
- PHYSICAL WORLDBook:NARAYNAChapter:PHYSICAL WORLDExercise:C.U.Q
Explore 10 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION Book:NARAYNAChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTION Exercise:EXERCISE - IV
Explore 39 Videos
Similar Questions
A string is wrapped several times on a cylinder of mass M and radius R. the cylinder is pivoted about its adxis of block symmetry. A block of mass m tied to the string rest on a support positioned so that the string has no slack. The block is carefully lifted vertically a distance h, and the support is removed as shown figure.
a. just before the string becomes taut evalute the angular velocity ω0 of the cylinder ,the speed v0 of the falling body, m and the kinetic energy K0 of the system.
b. Evaluate the corresponding quanitities ω1,v1 and K1 for the instant just after the string becomes taut.
c. Why is K1 less than K0? Where does the energy go?
d. If M=m, what fraction of the kinetic energy is lost when the string becomes taut?
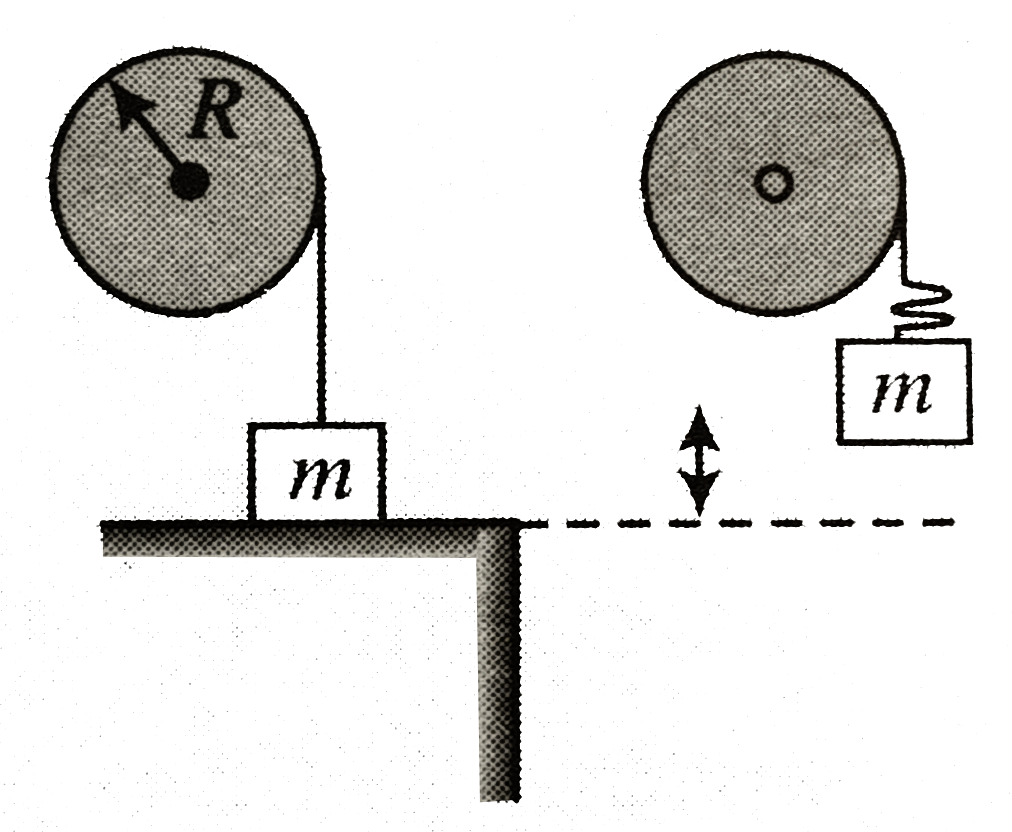
View SolutionA horizontal, homogeneous cylinder of mass M and radius R is pivoted about its axis of symmetry. A string is wrapped several times around the cylinder and tied to a body of mass m resting on a support positioned so that the string has no slack. The body of mass m is then lifted vertically to a distance h, and then released.
(a) Evaluate the angular velocity ω0 of the cylinder, the speed v0 of the falling body of mass m, and the kinetic energy K0 of the system, just before the string becomes taut.
(b) Evaluate the corresponding quantities, ω1,v1,andK1, for the instant just after the string becomes taut.
View Solution
Knowledge Check
A string is wrapped several time on a cylinder of mass M and radius R, the cylinder is pivoted about its axis of symmetery . A block mass of m tied to the string rests on support so that the string is black. The block is lifted upto a height h and the support is removed. (shown in figure)
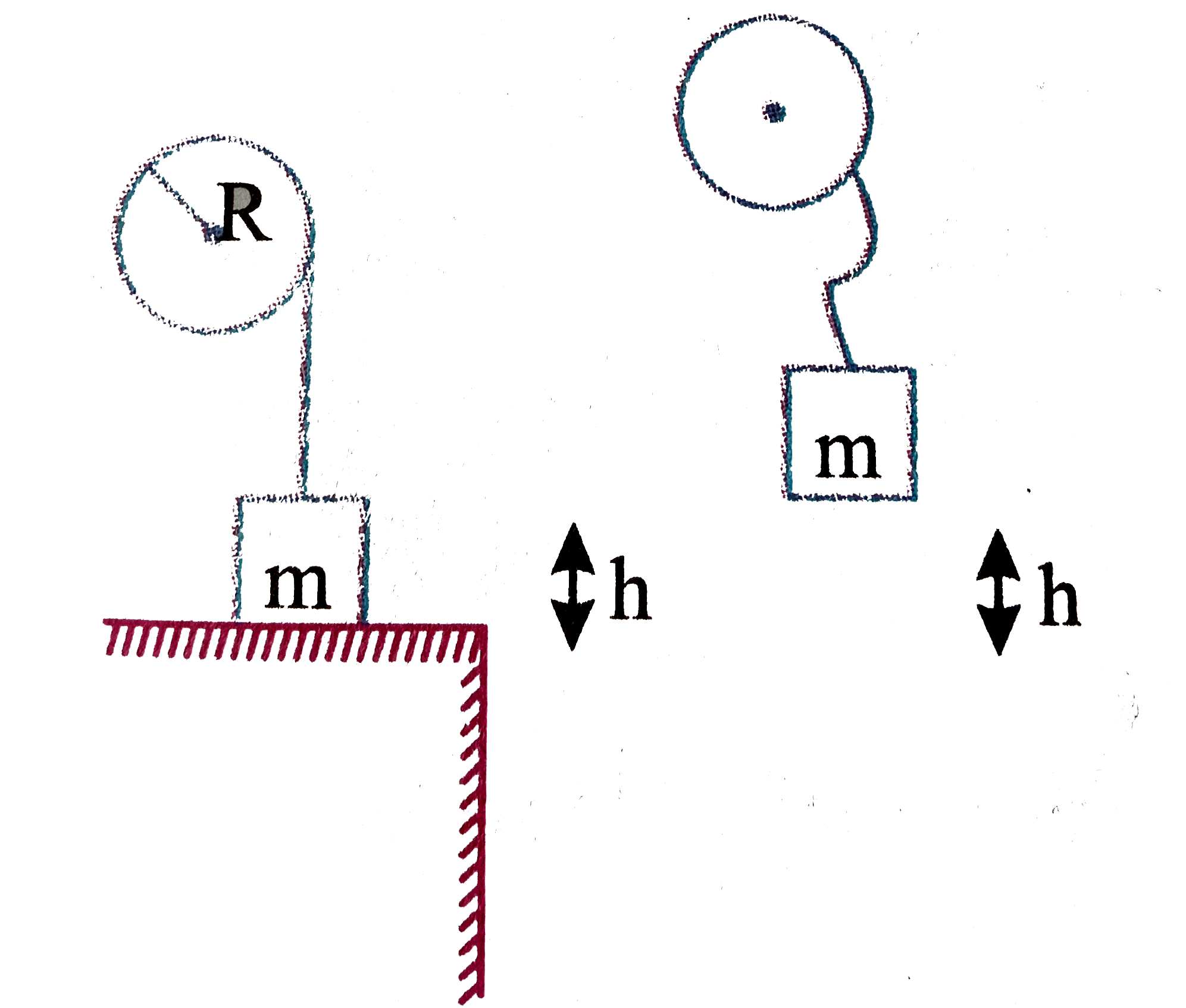
What is the angular velocity of cylinder just before the string becomes tautAzeroB√2ghRC√ghRD√ghRA string is wrapped several time on a cylinder of mass M and radius R, the cylinder is pivoted about its axis of symmetery . A block mass of m tied to the string rests on support so that the string is black. The block is lifted upto a height h and the support is removed. (shown in figure)
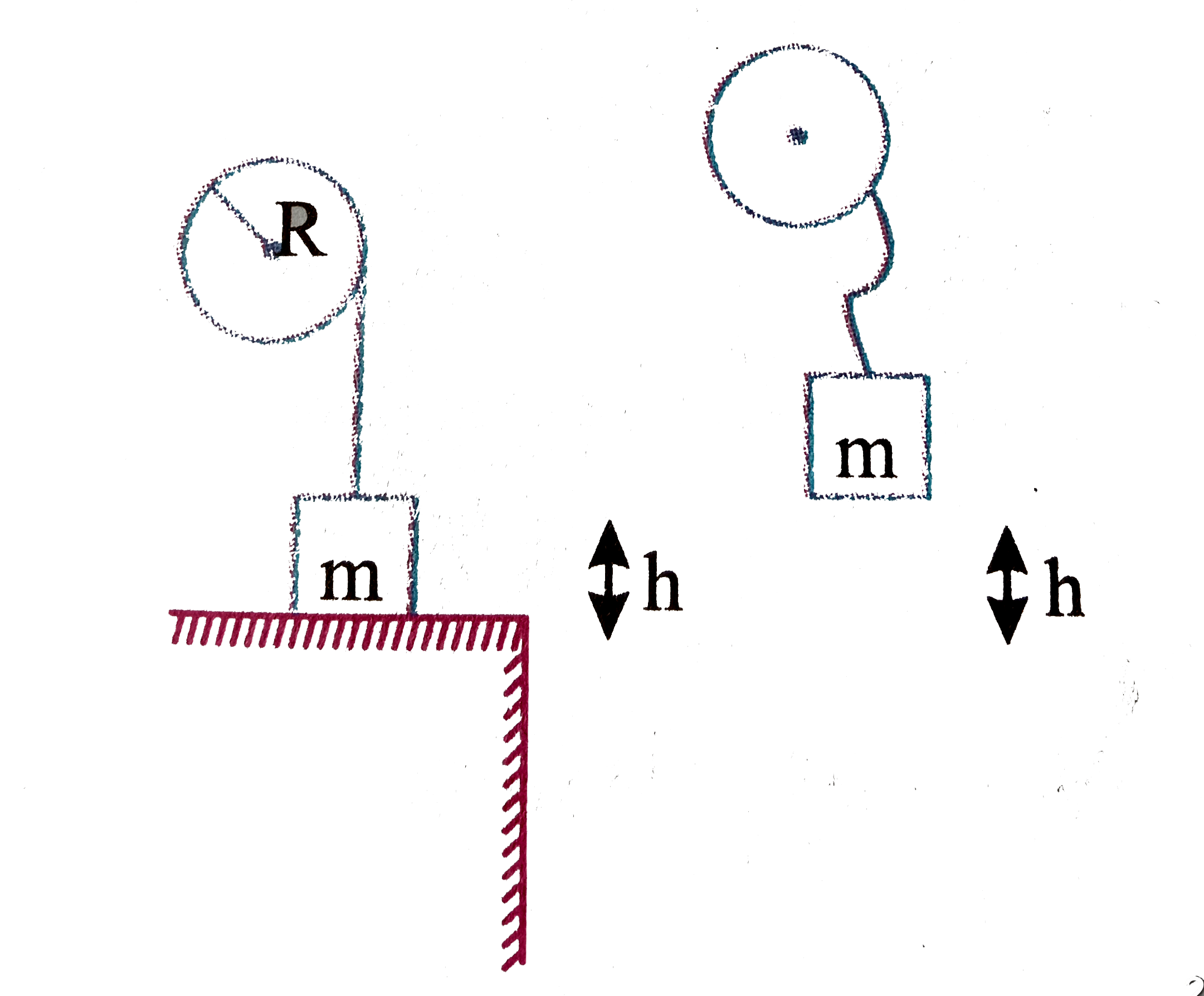
When the string experience a jerk, a large impulsive force is generated for a short duration, so that contribution of weight mg can be neglected suring this duration. then what will be speed of blocks m, just after string has becomes tautA√2gh[1+Mm]B√2gh[1+M2m]C√gh[1+Mm]D√gh[1+M2m]A string is wrapped around a cylinder of mass M and radius R. The string is pulled vertically upwards to prevent the centre of mass from falling as the cylinder unwinds the string. The tension in the string is
A2Mg/3BMg/2CMg/3DMg/6
A string is wrapped around a cylinder of mass M and radius R. The string is pulled vertically upwards to prevent the centre of mass from falling as the cylinder unwinds the string. The tension in the string is
View SolutionA string of negligible mass is wrapped on a cylindrical pulley of mass M and radius R. The other end of string is tied to a bucket of mass m. If the pulley rotates about a horizontal axis then the tension in the string is :
View SolutionA string wrapped around a cyliner of mass m and radius R. The end of the string is connected to block of same mass hanging vertically. No friction exists between the horizontal surface and cylinder.
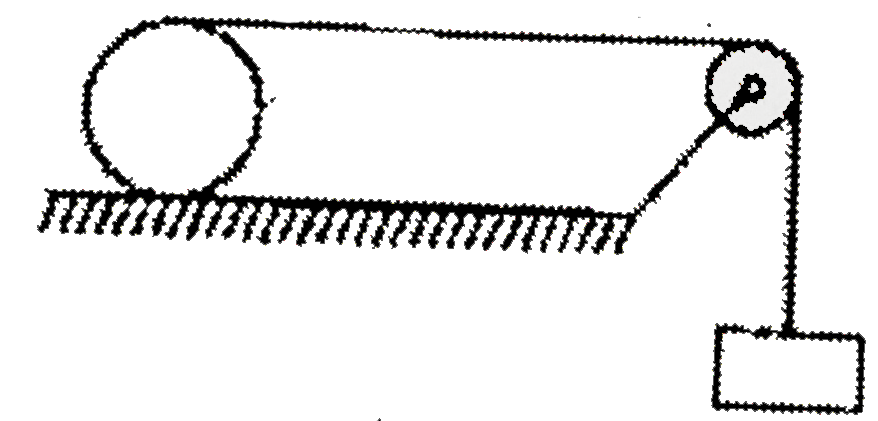
Velocity of point of contact 'of cylinder at this moment is:
View SolutionA string wrapped around a cyliner of mass m and radius R. The end of the string is connected to block of same mass hanging vertically. No friction exists between the horizontal surface and cylinder.
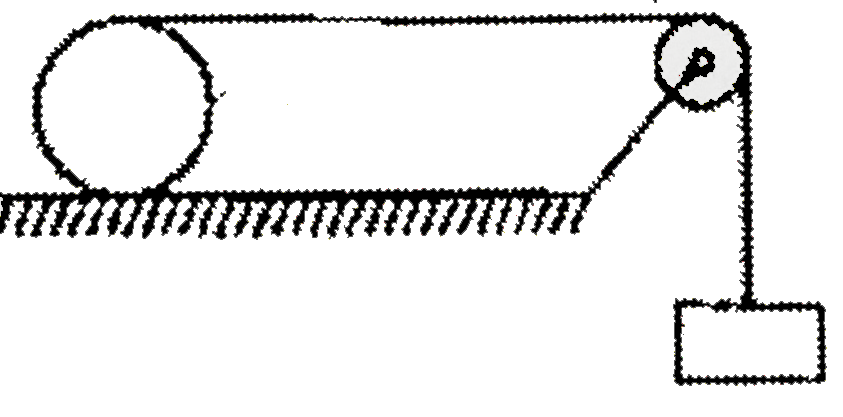
Acceleration of cylinder is:
View SolutionA string wrapped around a cyliner of mass m and radius R. The end of the string is connected to block of same mass hanging vertically. No friction exists between the horizontal surface and cylinder.
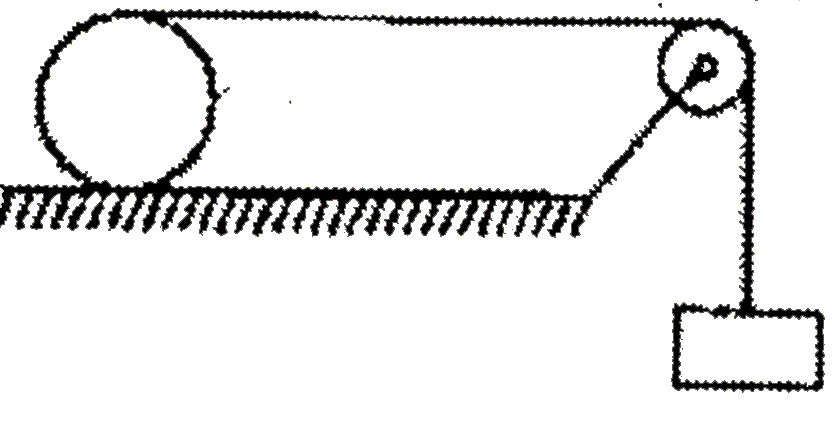
Acceleration of hanging mass is:
View Solution

