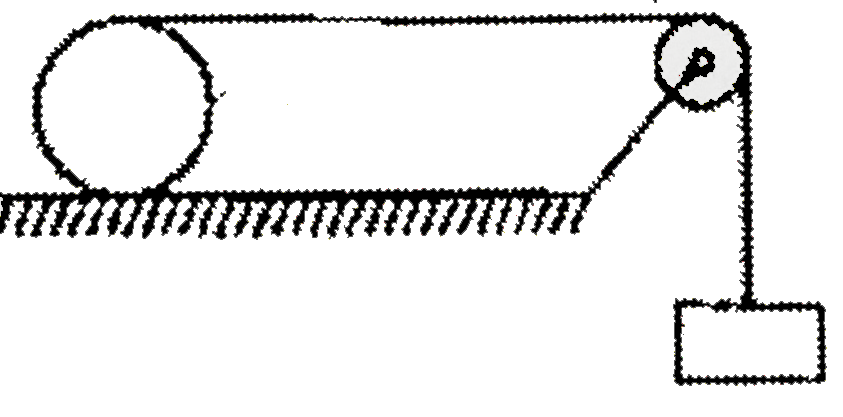
A string of negligible mass is wrapped on a cylindrical pulley of mass M and radius R. The other end of string is tied to a bucket of mass m. If the pulley rotates about a horizontal axis then the tension in the string is :
mg
(M+m)g
Mmg(M+2m)
2mg(M+2m)
The correct Answer is:C
To find the tension in the string wrapped around a cylindrical pulley with a bucket hanging from it, we can follow these steps:
Step 1: Identify the forces acting on the bucket
The forces acting on the bucket of mass m are:
- The gravitational force downward, which is mg (where g is the acceleration due to gravity).
- The tension T in the string acting upward.
Step 2: Write the equation of motion for the bucket
Since the bucket is accelerating downwards, we can write the equation of motion as:
mg−T=ma
where a is the acceleration of the bucket.
Step 3: Identify the torque acting on the pulley
The tension T in the string creates a torque on the pulley. The torque τ can be expressed as:
τ=T⋅R
where R is the radius of the pulley.
Step 4: Relate torque to angular acceleration
The torque is also related to the angular acceleration α of the pulley by the equation:
τ=I⋅α
where I is the moment of inertia of the pulley. For a solid cylinder, the moment of inertia I is given by:
I=12MR2
Thus, we can write:
T⋅R=12MR2⋅α
Step 5: Relate linear acceleration to angular acceleration
The linear acceleration a of the bucket is related to the angular acceleration α of the pulley by:
a=Rα
Substituting this into the torque equation gives:
T⋅R=12MR2⋅aR
Simplifying this, we find:
T=12Ma
Step 6: Substitute a back into the equation of motion
Now we have two equations:
1. mg−T=ma
2. T=12Ma
Substituting T from the second equation into the first gives:
mg−12Ma=ma
Rearranging this leads to:
mg=ma+12Ma
Factoring out a:
mg=a(m+12M)
Solving for a:
a=mgm+12M
Step 7: Substitute a back to find T
Now substitute a back into the equation for T:
T=12Ma=12M⎛⎝mgm+12M⎞⎠
This simplifies to:
T=Mmg2(m+12M)=Mmg2m+M
Final Answer
Thus, the tension in the string is:
T=Mmg2m+M
The forces acting on the bucket of mass m are:
- The gravitational force downward, which is mg (where g is the acceleration due to gravity).
- The tension T in the string acting upward.
Since the bucket is accelerating downwards, we can write the equation of motion as:
mg−T=ma
where a is the acceleration of the bucket.
The tension T in the string creates a torque on the pulley. The torque τ can be expressed as:
τ=T⋅R
where R is the radius of the pulley.
The torque is also related to the angular acceleration α of the pulley by the equation:
τ=I⋅α
where I is the moment of inertia of the pulley. For a solid cylinder, the moment of inertia I is given by:
I=12MR2
Thus, we can write:
T⋅R=12MR2⋅α
The linear acceleration a of the bucket is related to the angular acceleration α of the pulley by:
a=Rα
Substituting this into the torque equation gives:
T⋅R=12MR2⋅aR
Simplifying this, we find:
T=12Ma
Now we have two equations:
1. mg−T=ma
2. T=12Ma
mg−12Ma=ma
Rearranging this leads to:
mg=ma+12Ma
Factoring out a:
mg=a(m+12M)
Solving for a:
a=mgm+12M
Now substitute a back into the equation for T:
T=12Ma=12M⎛⎝mgm+12M⎞⎠
This simplifies to:
T=Mmg2(m+12M)=Mmg2m+M
Thus, the tension in the string is:
T=Mmg2m+M
Similar Questions

Consider the arrangement shown in figure. The string is wrapped around a uniform cylinder which rolls without slipping. The other end of the string is passed over a masslessm frictionless pulley to a falling weight, determine the acceleration of the falling mass m in terms of only the mass of the cylinder M, the mass m and g
View SolutionA string wrapped around a cyliner of mass m and radius R. The end of the string is connected to block of same mass hanging vertically. No friction exists between the horizontal surface and cylinder.
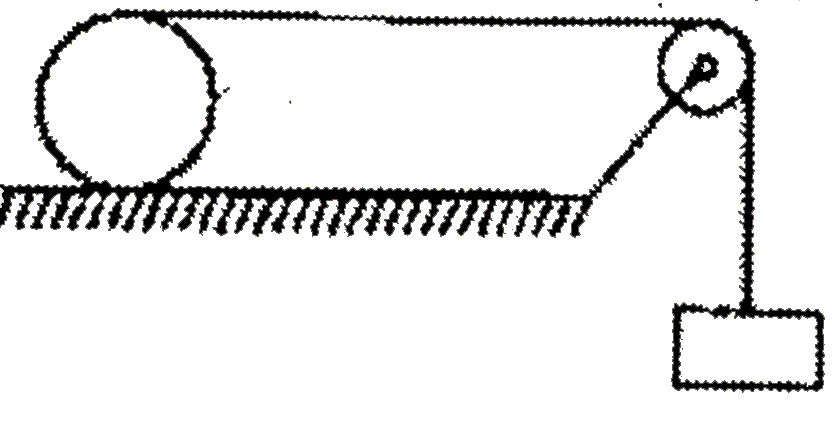
Acceleration of hanging mass is:
View Solution
Knowledge Check
A string is wrapped around a cylinder of mass M and radius R. The string is pulled vertically upwards to prevent the centre of mass from falling as the cylinder unwinds the string. The tension in the string is
A2Mg/3BMg/2CMg/3DMg/6A string is wrapped around a cylinder of mass M and radius R. The string is pulled vertically upwards to prevent the centre of mass from falling as the cylinder unwinds the string. The tension in the string is
AMg6BMg3CMg2D2Mg3An ideal inextensible string is wrapped over the disc of mass m and radius R. The other end of the string is connected to mass m. the string is passing over an ideal pulley A as shown in the figure. At any time t, mass m and disc are moving downward with acceleration of magnitude a1 and a2 respectively. The disc is rotating clockwise with angular acceleration of magnitude α . There is no slipping betweeb string and disc. choose the incorrect option
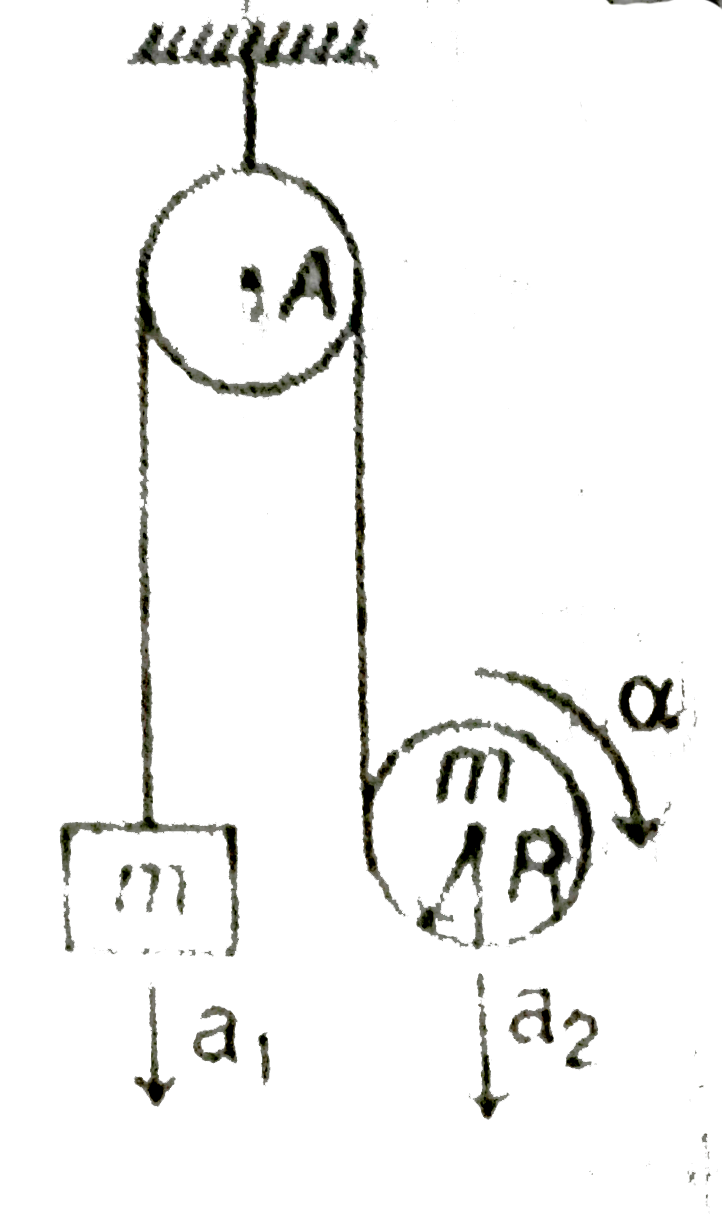 Aa1=a2BαR>a1CαR=a1DαR<a2
Aa1=a2BαR>a1CαR=a1DαR<a2
A stone of mass 50 g is tied to the end of a string 2 m long and is set into rotation in a horizontal circle with a uniforn speed of 2m/s .Then tension in the string is
View SolutionA string wrapped around a cyliner of mass m and radius R. The end of the string is connected to block of same mass hanging vertically. No friction exists between the horizontal surface and cylinder.
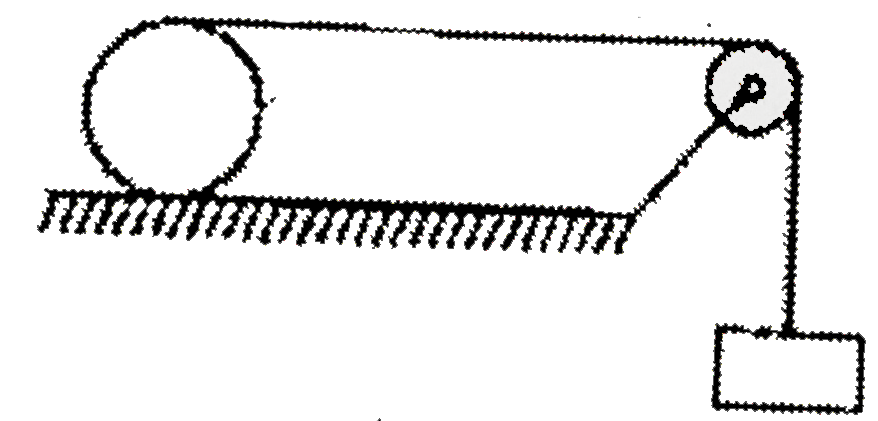
Velocity of point of contact 'of cylinder at this moment is:
View SolutionA string wrapped around a cyliner of mass m and radius R. The end of the string is connected to block of same mass hanging vertically. No friction exists between the horizontal surface and cylinder.
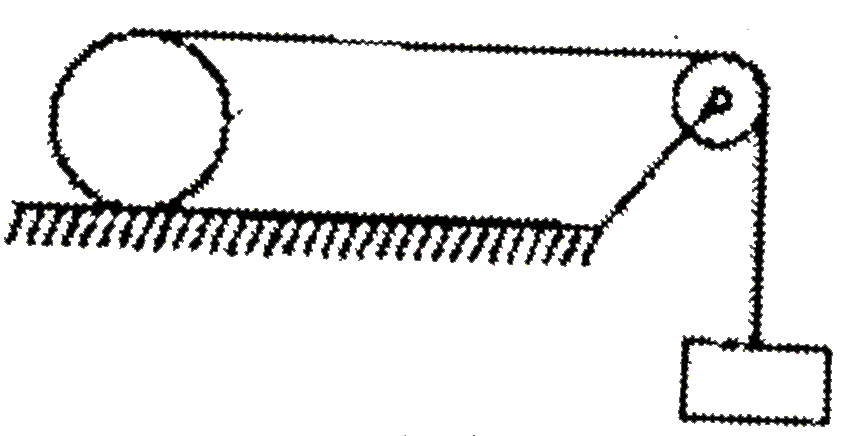
Velocity of hanging block at this moment is: is:
View SolutionA string wrapped around a cyliner of mass m and radius R. The end of the string is connected to block of same mass hanging vertically. No friction exists between the horizontal surface and cylinder.
Acceleration of cylinder is:
View SolutionA string of length L is fixed at one end and carries a mass M at the other end. The string makes 2/π revolution per second around the vertical axis through the fixed end as shown in the figure, then tension in the string is.

View Solution