
Consider the arrangement shown in figure. The string is wrapped around a uniform cylinder which rolls without slipping. The other end of the string is passed over a masslessm frictionless pulley to a falling weight, determine the acceleration of the falling mass m in terms of only the mass of the cylinder M, the mass m and g
let T be the tension in the string and f the force of (static) friction, between the cylinder and the surface.
a1= acceleration of centre of mass of cylinder
towards right
a2= downward acceleration of block m
α= angular acceleration of cylinder (clockwise)
Acceleration equations
for block mg−T=ma2
for cylinder T+f=Ma1 ..(ii)
α=(T−f)R12MR2 ..(iii)
Contact equations
The string is attached to the mass m at the highest point of the cylinder, hence
vm=vCOM+Rω ..
differentiating we get a2=a1+Rα ..(iv)
We also have (for rolling without slipping)
a1=Rα ..(v)
Solving these equations, we get
a2=8mg3M+8m
alternate solution (energy methode)
since, there is not slipping at all contact mechanical energy of the system will remain conserved.
∴ decrease in gravitational potential energy of block m in time t= increase in translational kinetic energy of block + increase in rotational as well as translational kinetic energy of cylinder
∴mgh=12mv22+12Iω2+12Mv21
or mg(12a2t2)=12m(a2t)2+12(12MR2)(αt)2+12M(a1t)2 ..(vi)
Solving Eqs. (iv) (V) and (vi) we get the same result.
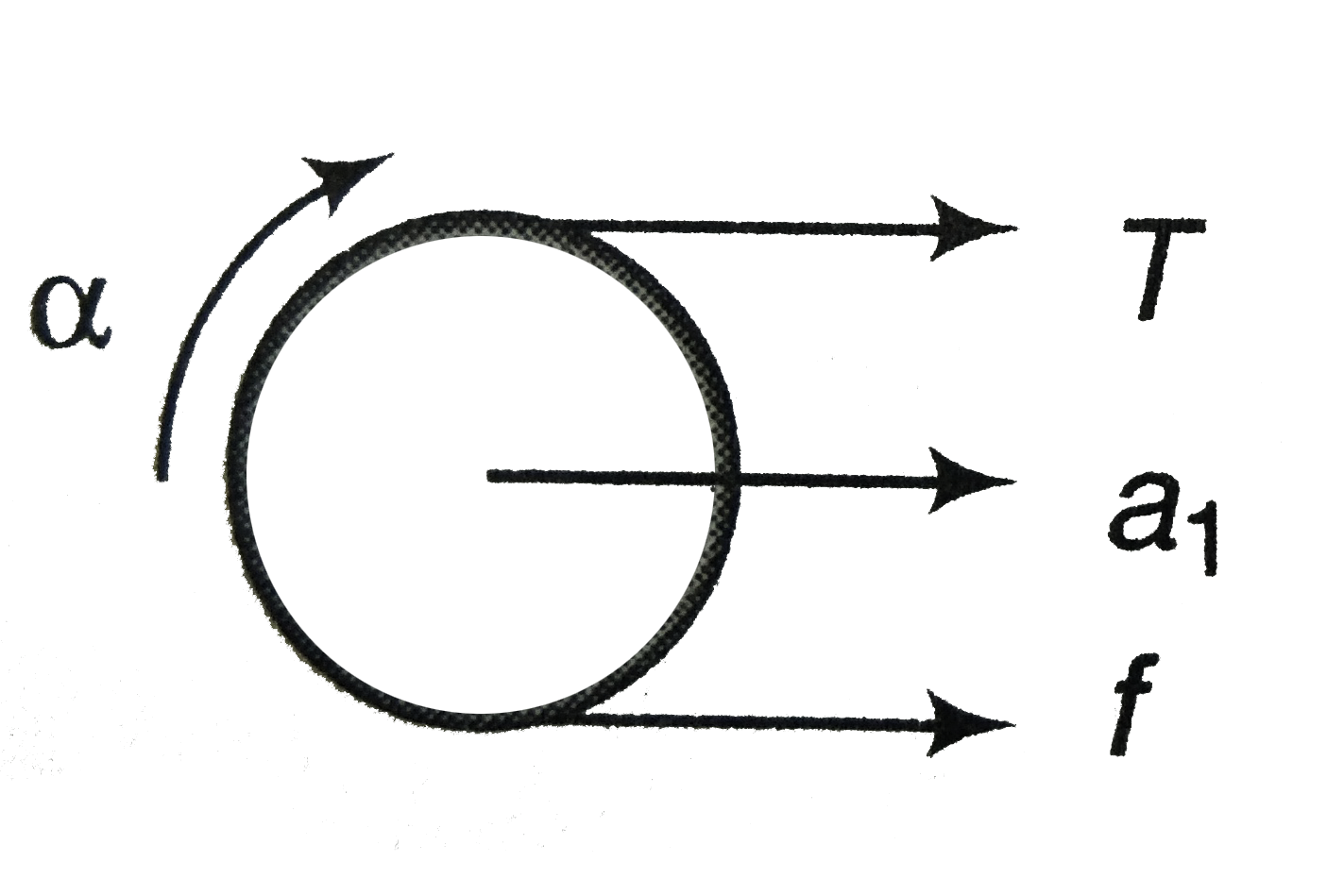

Topper's Solved these Questions
- ROTATIONAL MECHANICSBook:DC PANDEYChapter:ROTATIONAL MECHANICSExercise:Miscellaneous Examples
Explore 2 Videos
- ROTATIONAL MECHANICSBook:DC PANDEYChapter:ROTATIONAL MECHANICSExercise:Solved Example
Explore 1 Video
- ROTATIONAL MECHANICSBook:DC PANDEYChapter:ROTATIONAL MECHANICSExercise:Subjective Questions
Explore 2 Videos
- ROTATIONBook:DC PANDEYChapter:ROTATIONExercise:(C) Chapter Exercises
Explore 39 Videos
- ROTATIONAL MOTIONBook:DC PANDEYChapter:ROTATIONAL MOTIONExercise:Integer Type Questions
Explore 17 Videos
Similar Questions
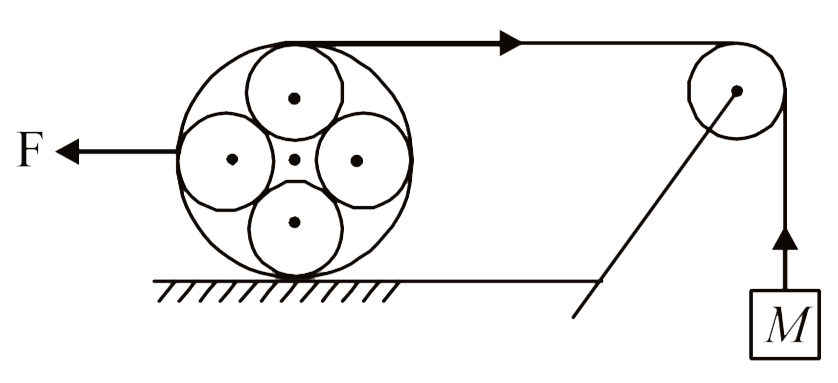
Four identical spheres having mass M and radius R are fixed tightly within a massless ring such that the centres of all spheres lie in the plane of ring. The ring is kept on a rough horizontal table as shown. The string is wrapped around the ring can roll without slipping. The other end of the string is passed over a massless frictionless pulley to a block of mass M. A force F is applied horizontally on the ring, at the same level as the centre, so that the system is in equilibrium.
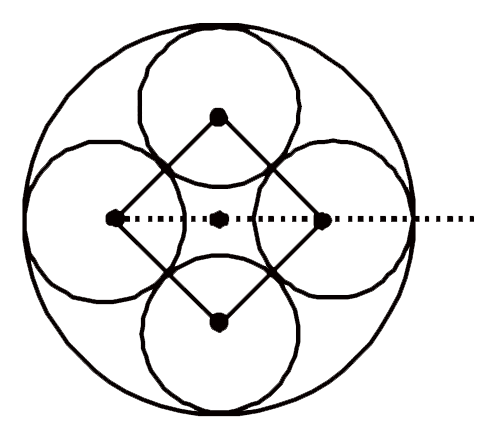
The magnitude of F is
View SolutionFour identical spheres having mass M and radius R are fixed tightly within a massless ring such that the centres of all spheres lie in the plane of ring. The ring is kept on a rough horizontal table as shown. The string is wrapped around the ring can roll without slipping. The other end of the string is passed over a massless frictionless pulley to a block of mass M. A force F is applied horizontally on the ring, at the same level as the centre, so that the system is in equilibrium.
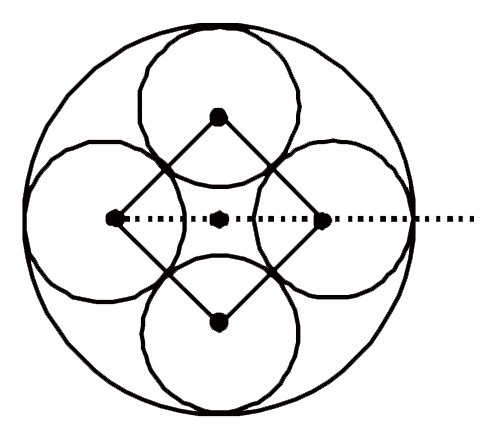
The moment of inertia of the combined ring system about the centre of ring will be
View Solution
Knowledge Check
Two particles of masses m and M(M>m) are connected by a cord that passes over a massless, frictionless pulley. The tension T in the string and the acceleration a of the particles is
AT=2mM(M−m)g,aMm(M+m)gBT=2mM(M+m)g,a=(M−mM+m)gCT=(M−mM+m)g,a=(2mM(M+m))gDT=(Mm(M+m)g,a=(2mM(M+m))gTwo masses m and m (m>m) are connected by massless flexible and inextensible string passed over massless and frictionless pulley. The acceleration of centre of mass is
A(m1−m2m1+m2)2gBm1−m2m1+m2gCm1+m2m1−m2gDZeroA string wrapped around a cyliner of mass m and radius R. The end of the string is connected to block of same mass hanging vertically. No friction exists between the horizontal surface and cylinder.
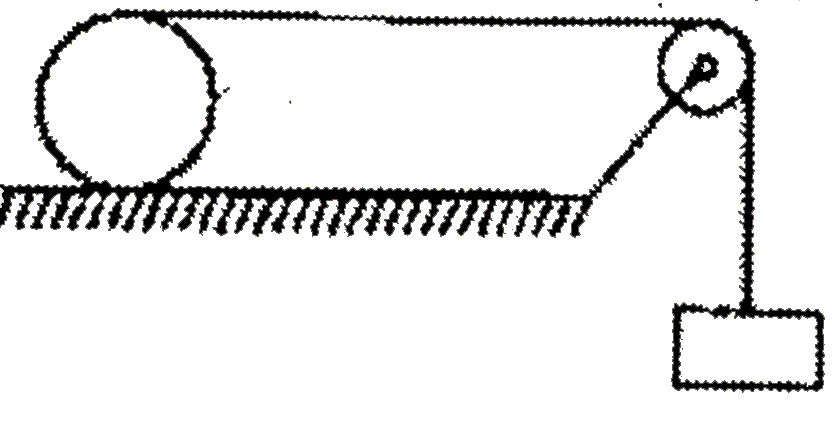
Acceleration of hanging mass is:AgBg2Cg4D3g4
Two masses M and m are connected at the two ends of an inextensible string. The string passes over a smooth frictionless pulley. Calculate the acceleration of the masses and the tension in the string. Given M>m.
View SolutionA string of negligible mass is wrapped on a cylindrical pulley of mass M and radius R. The other end of string is tied to a bucket of mass m. If the pulley rotates about a horizontal axis then the tension in the string is :
View SolutionA uniform cylinder free to turn around a fixed axis has a string wrapped around it as shown. The string is pulled with a force F equal to the cylinders weight. What is the acceleration of the string?
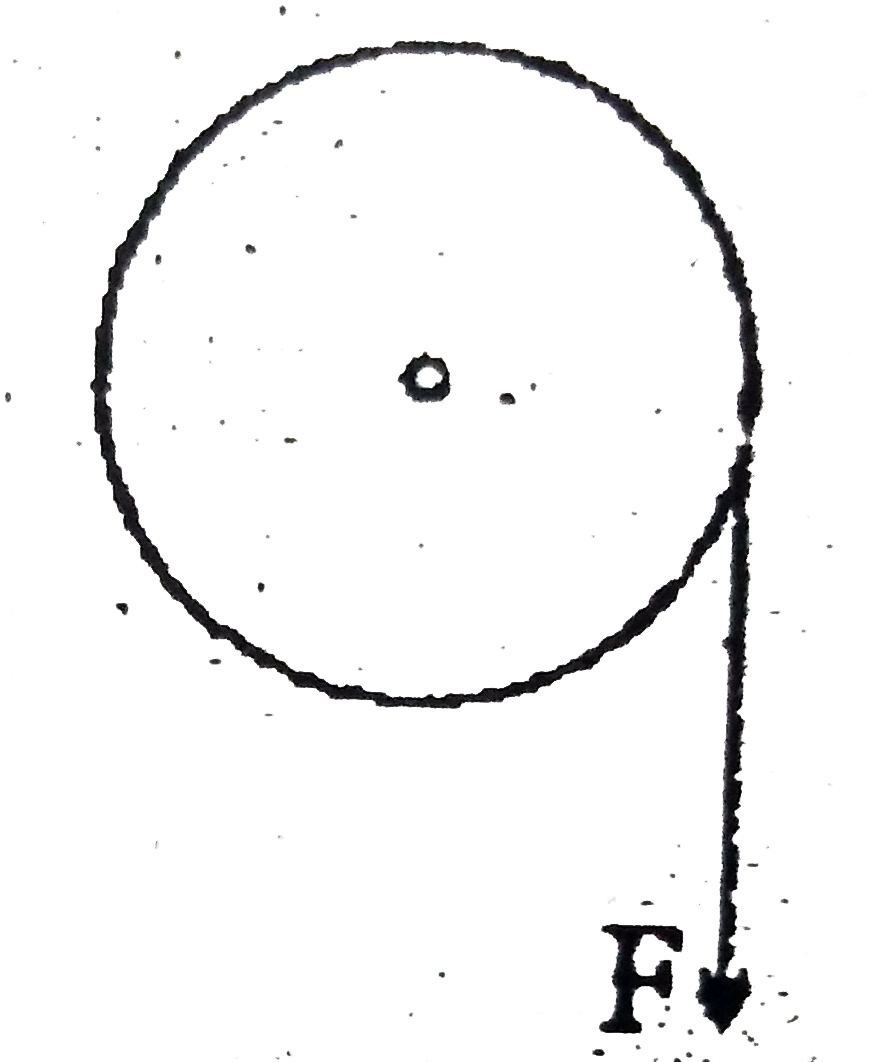
View SolutionA string is wrapped around a cylinder of mass M and radius R. The string is pulled vertically upwards to prevent the centre of mass from falling as the cylinder unwinds the string. The tension in the string is
View SolutionA string wrapped around a cyliner of mass m and radius R. The end of the string is connected to block of same mass hanging vertically. No friction exists between the horizontal surface and cylinder.
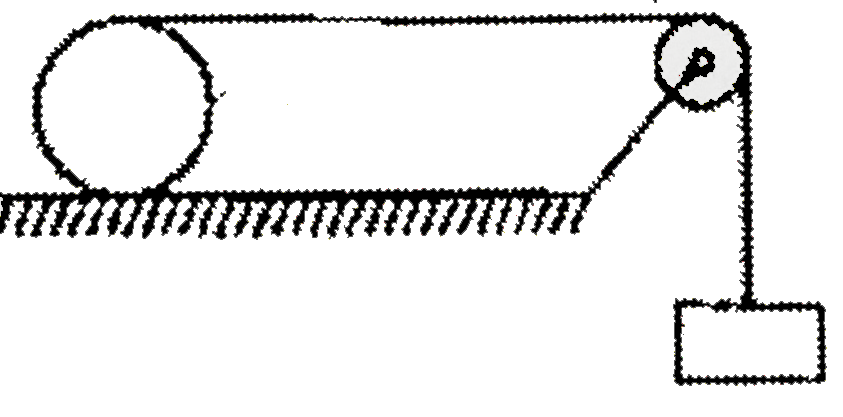
Acceleration of cylinder is:
View Solution

