Two uniform thin rods A and B of length 0.6 m each and of masses 0.01 kg and 0.02kg respectively are rigidly joined end to end. The combination is pivoted at the lighter end, P as shown in fig. Such that it can freely rotate about point P in a vertical plane. A small object of mass 0.05kg, moving horizontally, hits the lower end of the combination and sticks to it what should be the velocity of the object so that the system could just be reised to the horizontal position.
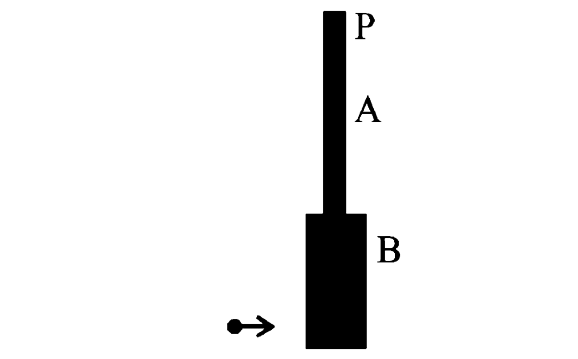


System is free to rotate but not free to translete. During collision net torque on the system (rod A+rodB+mass m ) about point P is zero
therefore, angular momentum of system before collision
= angular momentum of system just after collisio (about P)
Let ω be the angular velocity of system just after collision then
Li=Lf⇒mv(2l)=Iω ..(i)
=m(2l)2+mA(l2/3)+mB[l212+(l2+l)2]
given l=0.6m,m=0.05kg,mA=0.01kg and mB=0.02kg
Substituting the values we get
I=0.09kg−m2
therefore, from Eq. (i)
ω=2mvlI=(2)(0.05)(v)(0.6)0.09
ω=0.67v (ii)
Now after collision, mechanical energy will be conserved.
Therefore, decrease in rotational KE= increase in gravitational PE
or 12Iω2=mg(2l)+mAg(l2)+mBg(l+l2)
ω2=gl(4m+mA+3mB)I
=(9.8)(0.6)(4×0.05+0.01+3×0.02)0.09
=17.64(rad/s)2
∴ω=4.2rad/s ..(iii)
Equating Eqs. (ii) and (iii) we get
v=4.20.67m/s or v=6.3m/s
Topper's Solved these Questions
- ROTATIONAL MECHANICSBook:DC PANDEYChapter:ROTATIONAL MECHANICSExercise:Miscellaneous Examples
Explore 2 Videos
- ROTATIONAL MECHANICSBook:DC PANDEYChapter:ROTATIONAL MECHANICSExercise:Solved Example
Explore 1 Video
- ROTATIONAL MECHANICSBook:DC PANDEYChapter:ROTATIONAL MECHANICSExercise:Subjective Questions
Explore 2 Videos
- ROTATIONBook:DC PANDEYChapter:ROTATIONExercise:(C) Chapter Exercises
Explore 39 Videos
- ROTATIONAL MOTIONBook:DC PANDEYChapter:ROTATIONAL MOTIONExercise:Integer Type Questions
Explore 17 Videos
Similar Questions
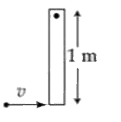
A thin rod of mass 0.9 kg and length 1 m is suspended , at rest form one end so that it can freely oscillate in the vertical plane. A particle of move 0.1 kg moving in a striaght line with velcoity 80 n/s hits the rod at is bottom most point and sticks to it (see figure) . The angluar speed ( in rad/s) of the rod immediately after the collision will be .
View SolutionA uniform rod ofmass M and length L is hanging from its one end free to rotate in a veritcal plane.A small ball of equal mass is attached of the lowe end as shown. Time period of small oscillations of the rod is

View Solution
Knowledge Check
A uniform rod of mass m and length l is hinged at upper end. Rod is free to rotate in vertical plane. A bail of mass m moving horizontally with velocity v0 collides at lower end of rod perpendicular to it and sticks to it. The minimum velocity of the ball such that combined system just completes the vertical circle will be
A2[√2gl]B√2glC2[√gl]D√glA slender rod is hinged at its top end and hanging freely in a vertical position. A tiny ball, moving horizontally, hits the lower end of the rod elastically and comes to rest. The ratio of the mass of rod to the mass of the ball must be
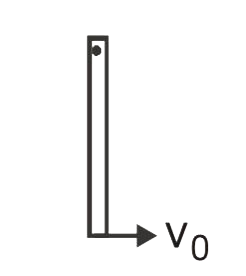
A3:2B3:1C5:3Dinsufficient dataA thin uniform rod is free to rotate about a fixed smooth horizontal axis as shown. A point mass hits horizontally with velocity v0 to the one end B of the rod. When it hits, it sticks to the rod, then :
 AMinimum value of v0 for the rod to rotate by an angle π2is2√gL .BAngular acceleration of the rod when the rod is horizontal is 9g8L .CForce applied by the axis on the rod in the horizontal state is 5mg/6 .Dfor a small velue of v0 the rod performes small oscillations with a period of 43π√lg
AMinimum value of v0 for the rod to rotate by an angle π2is2√gL .BAngular acceleration of the rod when the rod is horizontal is 9g8L .CForce applied by the axis on the rod in the horizontal state is 5mg/6 .Dfor a small velue of v0 the rod performes small oscillations with a period of 43π√lg
A thin uniform rigid rod of length L is hinged at one end so that it can move in a vertical plane by rotating about a horizontal axis through upper end. The lower end is given a sharp blow and made to acquire a linear velocityvo . Find the maximum height to which the lower end can rise.
View SolutionA ligh rod of length 1 m is pivoted at its centre and two masses of 5 kg and 2 kg are hung from the ends as shown in the figure. Find the initial angular acceleration of the rod assuming that it was horizontal in the beginning.

View SolutionA uniform rod of mass 20 Kg and length 1.6 m is piovted at its end and swings freely in the vertical plane. Angular acceleration of the rod just after the rod is relased from rest in the horizontal position is

View SolutionA thin uniform rigid rod of length l is hinged at one end so that it can move ina vertical plane by rotating about a horizontal axis through upper end. The lower end is given a sharp blow and made to acquire a linear velocity Maximum height attained by lower end of the rod is:

View SolutionA thin uniform rod of length l and mass m is freely pivoted about its end. The rod is initially held horizontally and released from rest. When the rod is vertical, an impulse J is applied to bring it to rest (this is in addition to any impulse provided by the pivot)

What is the angular velocity of the rod at the moment it reaches the vertical position ?
View Solution

