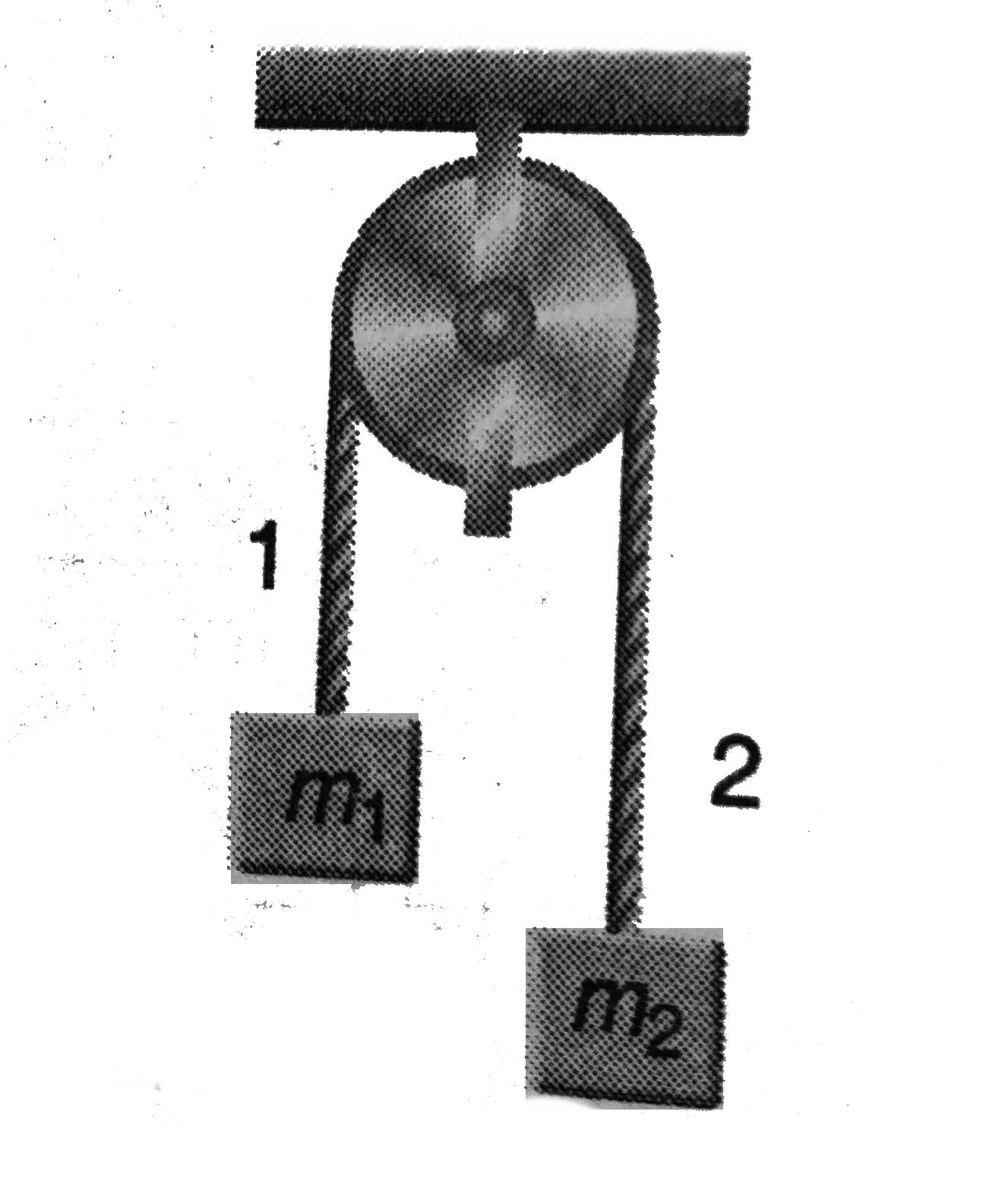
In the arrangement shown in figure the mass of the uniform solid cylindrical pulley of radius is equal to and the masses of two bodies are equal to and . The thread slipping and the friction in the axle of the pulley are supposed to be absent. Find the angular acceleration of the cylinder and the ratio of tensions of the vertical sections of the thread in the process of motion.
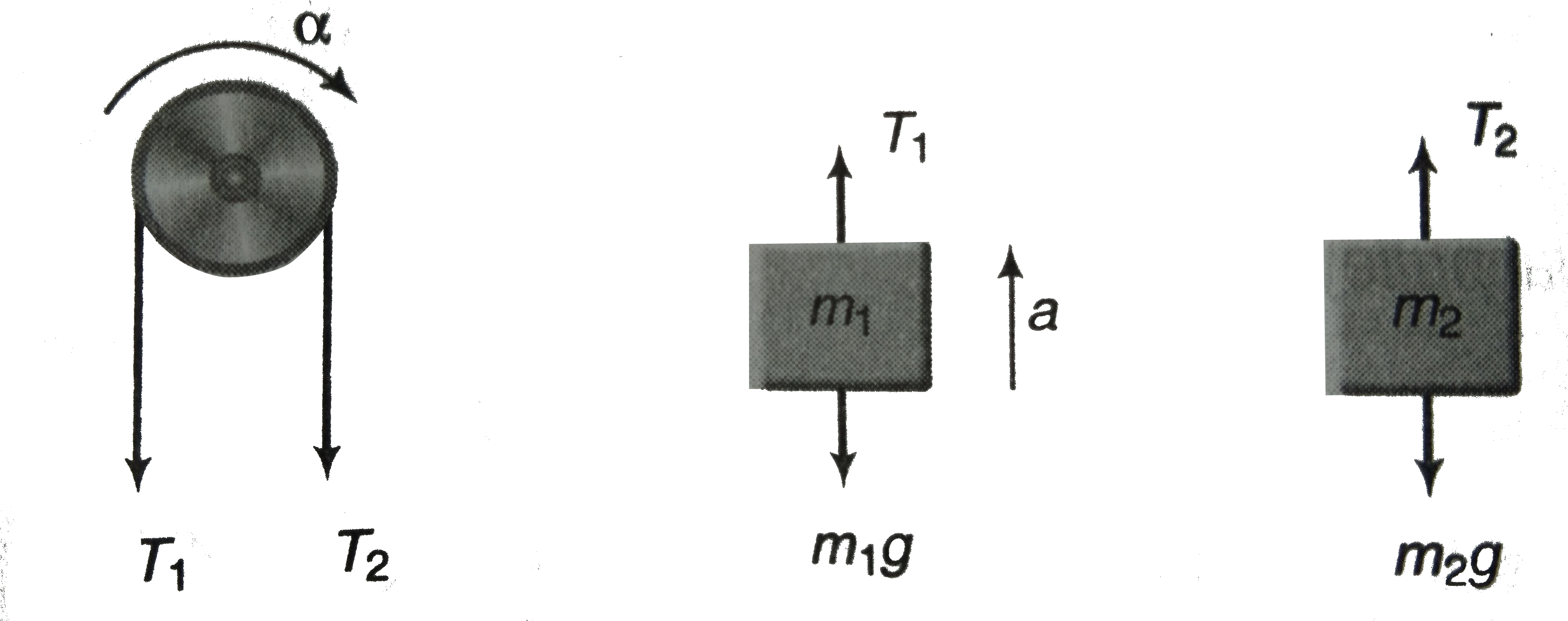
Let angular acceleration of the pulley and linear acceleration of two bodies
Equations of motion are
for mass ..(i)
for mass ..(ii)
for pulley
For no slipping condition ..(iv)
Solving these equation, we get
and
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Miscellaneous Examples
2 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Solved Example
1 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
- ROTATIONBOOK - DC PANDEYCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEYCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions
17 Videos
Similar Questions
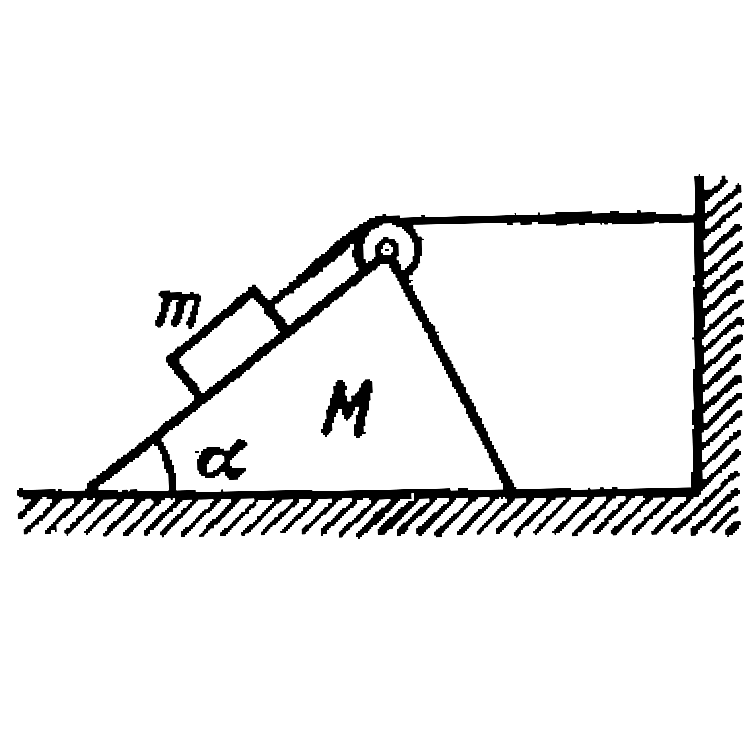
In the arrangement shown in figure the masses m of the bar and M of the wedge, as well as the wedge angle α, are known. The masses of the pulley and the thread are negligible. The friction is absent. Find the acceleration of the wedge M.
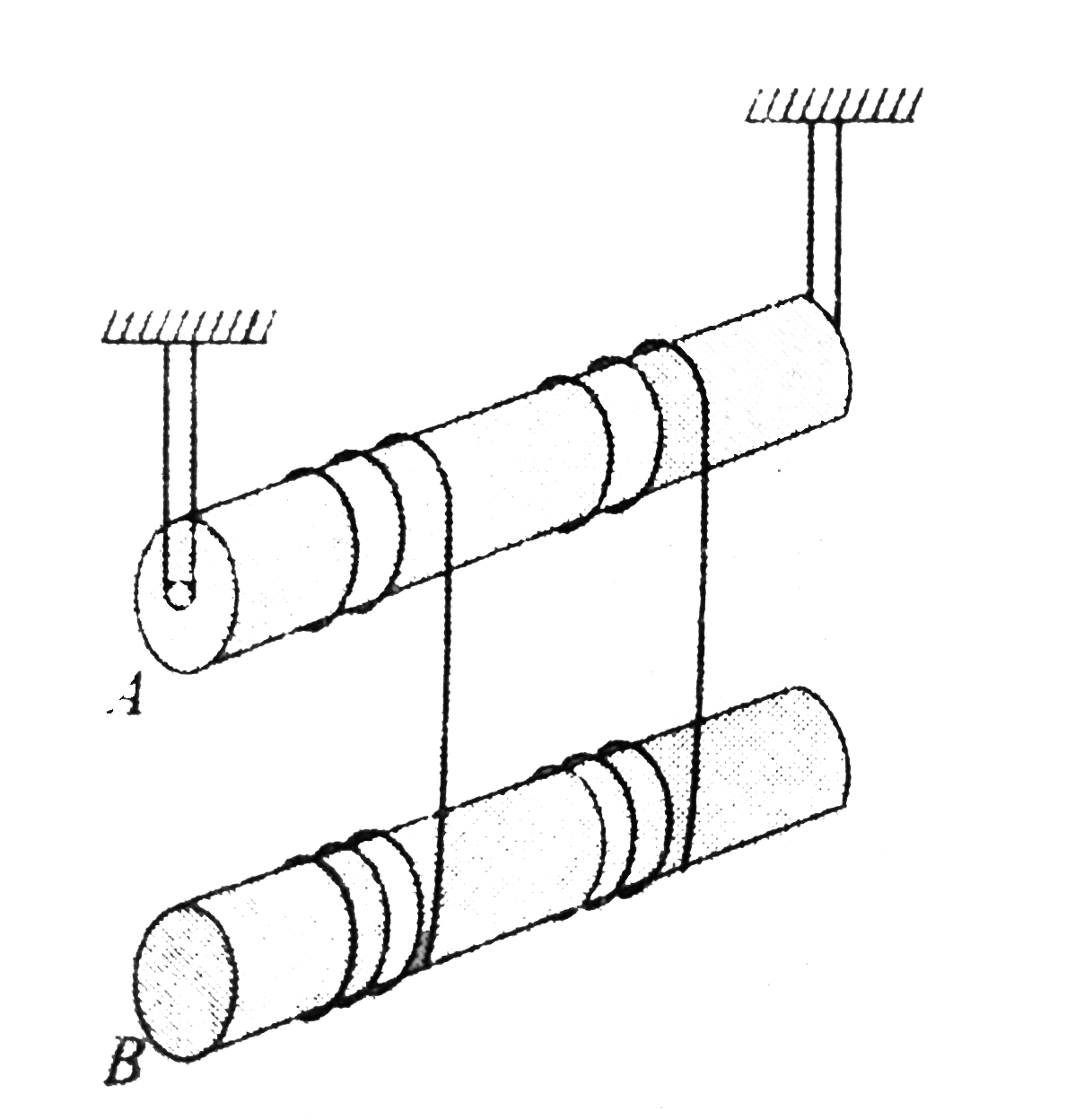
View SolutionThe arrangement shown in figure consists of two identical, uniform, solid cylinders, each of mass m, on which two light threads are wound symmetrically.
Find the tensions of each thread in the process of motion. The friction in the axle of the upper cylinder is assumed to be absent.
View Solution
Knowledge Check
Two bodies with masses m1 and m2(m1>m2) are joined by a string passing over fixed pulley. Assume masses of the pulley and thread negligible. Then the acceleration of the centre of mass of the system (m1+m2) is
A(a) (m1−m2m1+m2)gB(b) (m1−m2m1+m2)2gC(c) m1gm1+m2D(d) m2gm1+m2
In the arrangement shown in fig the bodies have masses m0,m1andm2 the friction is absent the masses of pulleys and the threads are negligible find the acceleration of the body m1
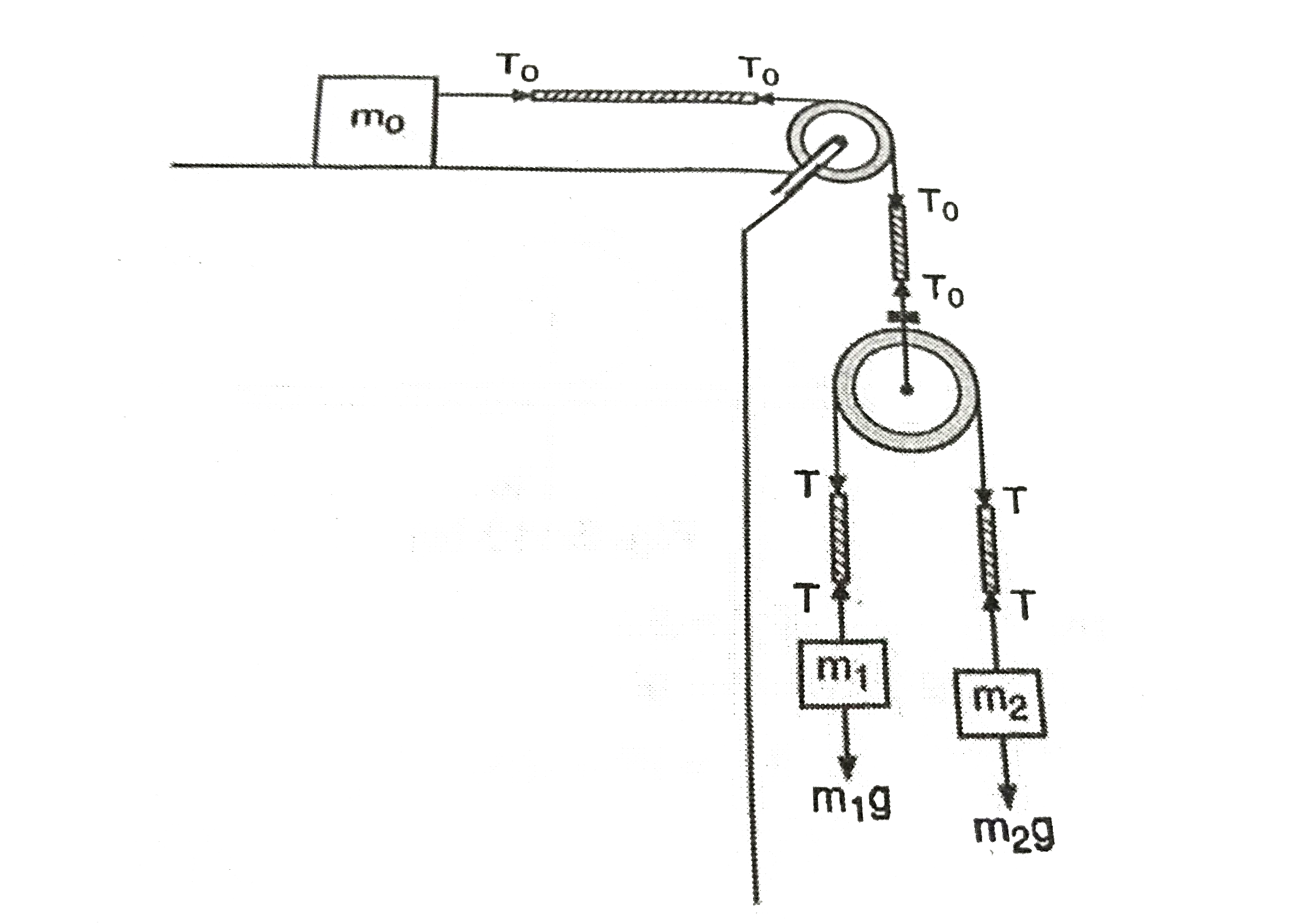
View SolutionA pulley fixed to the ceiling carries a thread with bodies of masses m1 and m2 attached at its ends. The masses of the pulley and thread are negligible, friction is absent. Find the acceleration of the centre of mass(acm) of this system.
View SolutionA pulley fixed to the ceiling carried a thread with bodies of masses m1 and m2 attached to its ends. The mases of the pulley and the thread are negligible and friction is absent. Find the acceleration of the centre of mass of this system.
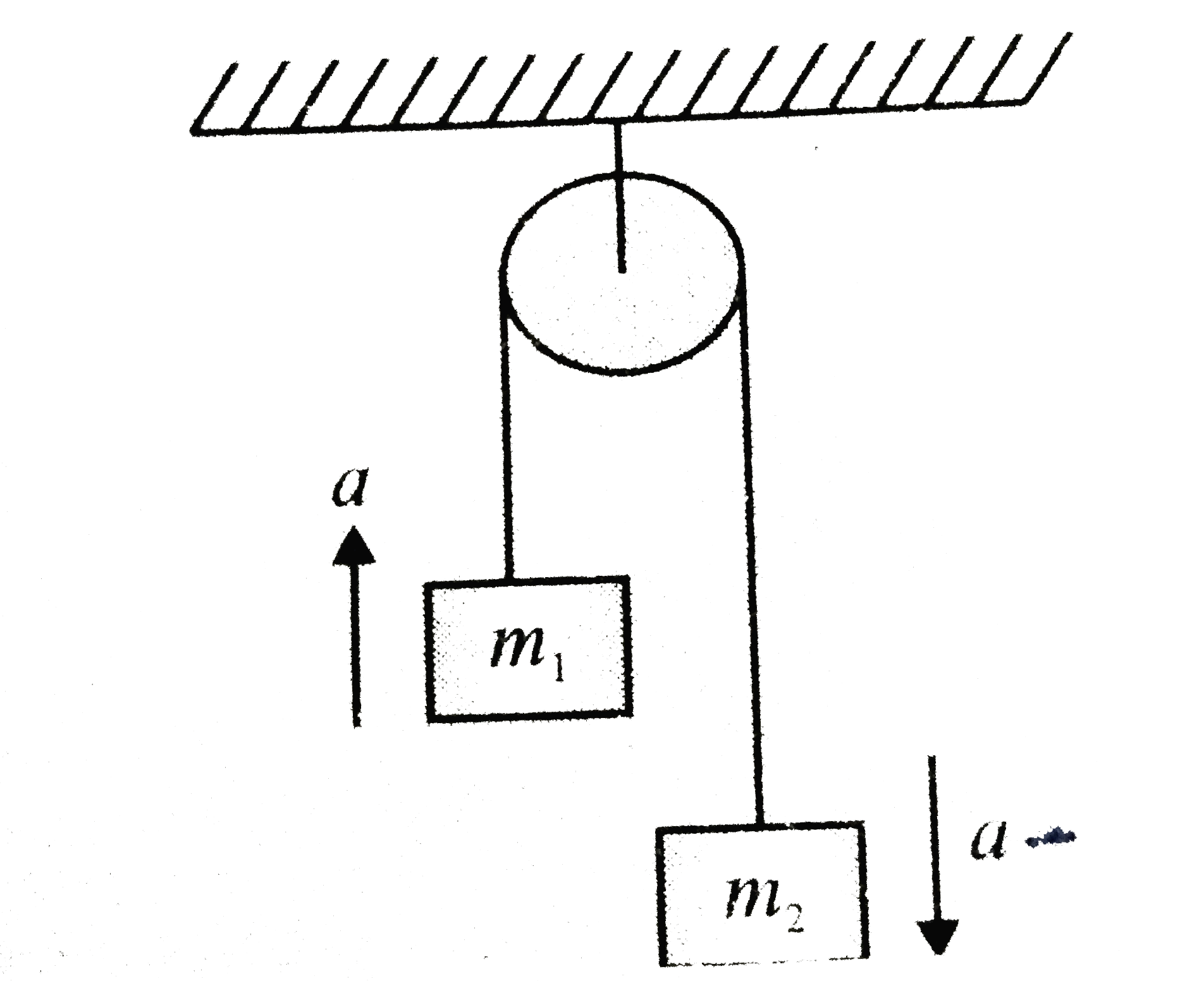
View SolutionIn the arrangement shown in figure the bodies have masses m0, m1, m2, the friction is absent, the masses of the pulleys and the threads are negligible. Find the acceleration of the body m1. Look into possible cases.

View SolutionA pulley fixed to the ceiling carries a thread with bodies of masses m1 and m2 attached to its ends. The masses of the pulley and the thread are negligible, friction is absent. Find the acceleration wC of the centre of inertia of this system.
View SolutionA rod AB of mass m is hung by two ideal threads. Find the ratio of tensions in the two threads (T1T2).
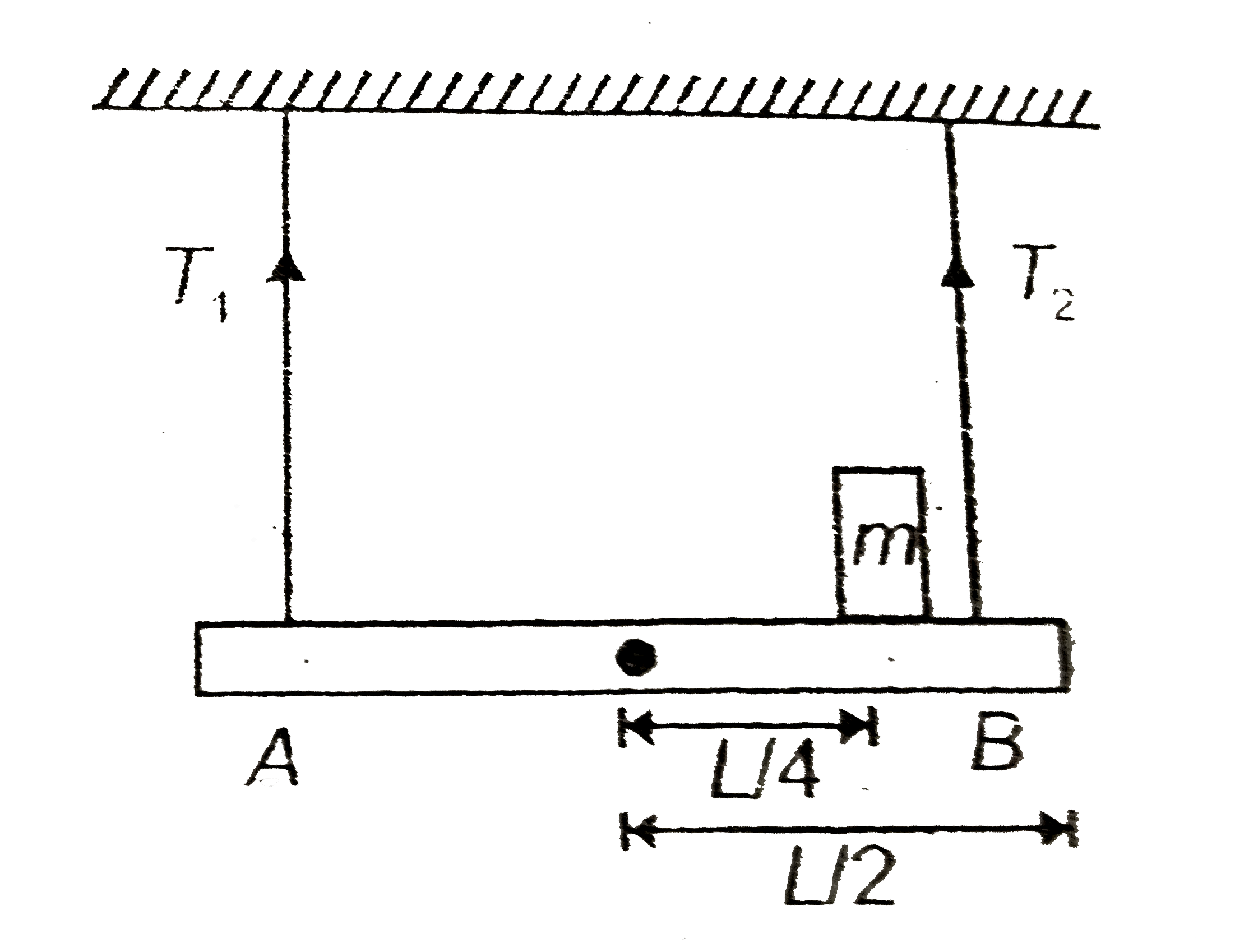
View SolutionIn the arrangement shown in figure the masses of the wedge M and the body m are known. The appreciable friction exists only between the wedge and the body m, the friction coefficient being equal to k. The masses of the pulley and the thread are negligible. Find the acceleration of the body m relative to the horizontal surface on which the wedge slides.

View Solution
