The arrangement shown in figure consists of two identical, uniform, solid cylinders, each of mass m, on which two light threads are wound symmetrically.
Find the tensions of each thread in the process of motion. The friction in the axle of the upper cylinder is assumed to be absent.

Let the lower cylinder go down by x when the upper cylinder A rotates through θ and the lower one rotates through θ'. Since both cylinders unwind themselves, therefore
x=R(θ+θ')
We can write a=R(α+α')

Where a=downward acceleration of A
α= angular acceleration of A
α'= angular acceleration of B
Considering the rotational motion of A
τ=2TR=(12MR2)×α⇒4TR
Considering the rotational motion of B
τ=2TR=(12mR2)×a'⇒α'=4TR
Considering the downward motion of B
mg−2T=ma
mg−2T=mR(α+α')=mR(4TR+4TR)
mg−2T=8T⇒T110mg
Topper's Solved these Questions
- RIGID BODY DYNAMICS 1Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 1Exercise:Solved Examples
Explore 9 Videos
- RIGID BODY DYNAMICS 1Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 1Exercise:Exercise 2.1
Explore 6 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBook:CENGAGE PHYSICSChapter:PROPERTIES OF SOLIDS AND FLUIDSExercise:INTEGER_TYPE
Explore 2 Videos
- RIGID BODY DYNAMICS 2Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 2Exercise:Interger
Explore 2 Videos
Similar Questions

In the arrangement shown in figure the mass of the uniform solid cylindrical pulley of radius R is equal to m and the masses of two bodies are equal to m1 and m2. The thread slipping and the friction in the axle of the pulley are supposed to be absent. Find the angular acceleration of the cylinder and the ratio of tensions T1T2 of the vertical sections of the thread in the process of motion.
View SolutionThin threads are tightly wound on the ends of a uniform solid cylinder of mass m. The free ends of the threads are attached to the ceiling of an elevator car. The car starts going up with an acceleration w0. Find the acceleration w′ . Find the acceleration w′ of the cylinder relative to the car and the force F exerted by the cylinder on the ceiling (through the threads).
View Solution
Knowledge Check
For the arrangement shown in the figure the coefficient of friction between the two blocks is μ. If both the blocks are identical and moving ,then the acceleration of each block is
 AF2m−2μgBF2mCF2m−μgDzero
AF2m−2μgBF2mCF2m−μgDzeroA uniform cylinder of mass m rests on two rough horizontal planks. A thread is wound on the cylinder. The hanging end of the thread is pulled vertically down with a constant force F
ASince horizontal acceleration is provided by the friction acting on the cylinder, its translation kinetic energy (12mv2) is equal to work done by this friction,BSince moment about instantaneous axis of rotation is produced by force F. kinetic energy (12Iω2) is equal to work done by F where I is moment of inertia about the instantaneous axis of rotation and ω is the-angular velocity.CSince cylinder is moving, energy is lost against friction.DWork done by F+ work done by friction on cylinder =totalKE of the cylinder.In the arrangement shown in figure two equal masses (each m) hung light cords wrapped around a uniform solid cylinder of mass M and radius R. The cylinder is free to roate about a harizontal axis. If the system is released from rest then, the tension in each cord is-
 AMmg4m+MBMmgm+MCMmgM+3mDMmg2m+M
AMmg4m+MBMmgm+MCMmgM+3mDMmg2m+M
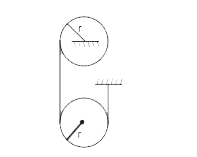
Two uniform cylinders, each of mass m=10 kg and radius r = 150 mm, are connected by a rough belt as shown. If the system is released from rest, determine
the tension in the portion of the belt connecting the two cylinders.
View SolutionA solid uniform cylinder of mass m performs small oscillations due to the action of two springs of stiffness k each (figure). Find the period of these oscillation in the absendce of sliding.
x
View SolutionA cylinder of mass m is suspended through two strings wrapped around it as shwon in figure . Find a. the tension T in the string and b. the speed o the cylinder as it falls through a distance h.

View SolutionA uniform solid. cylinder A of mass can freely rotate about a horizontal axis fixed to a mount of mass m2. A constant horizontal force F is applied to the end K of a light thread tightly wound on the cylinder. The friction between the mount and the supporting horizontal plane is assumed to be absent. Find the acceleration of the point K.
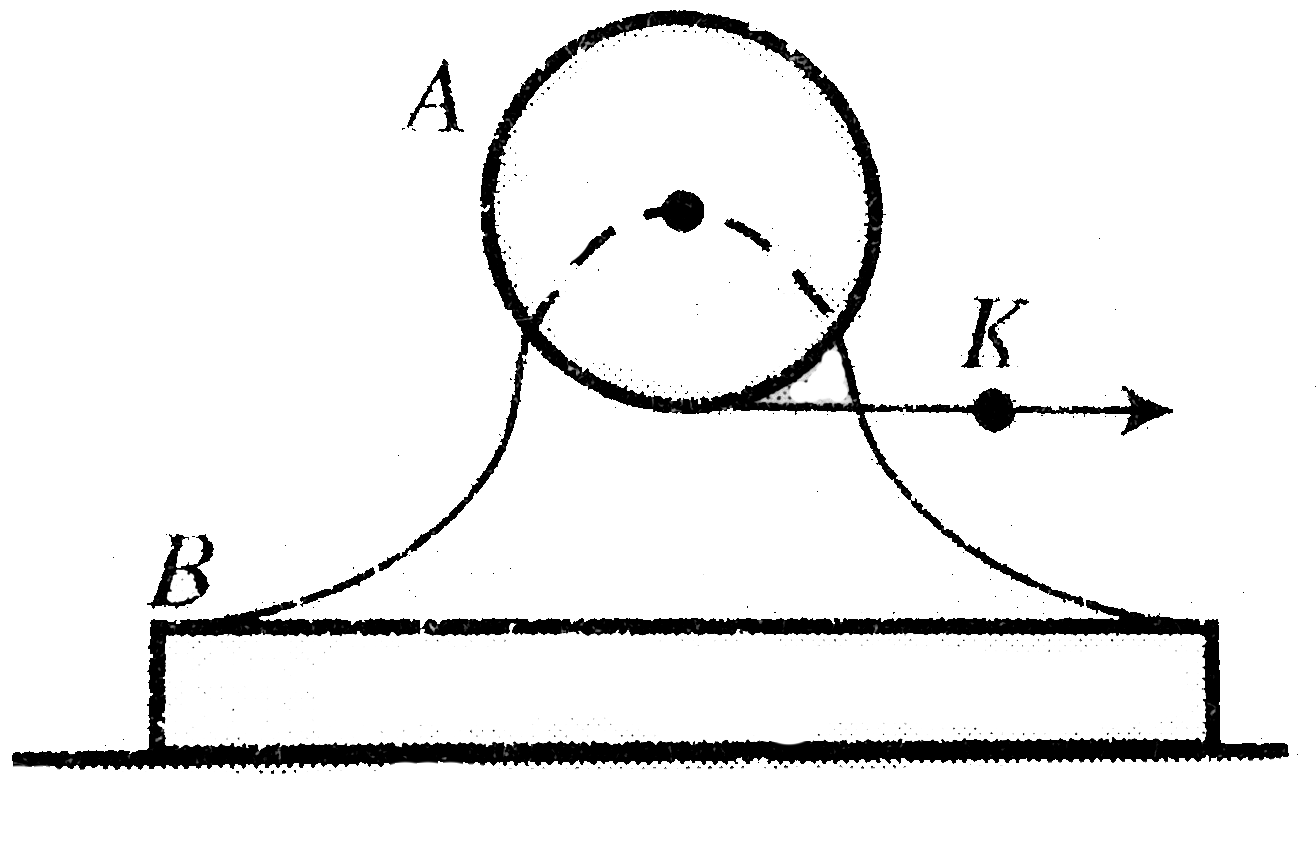
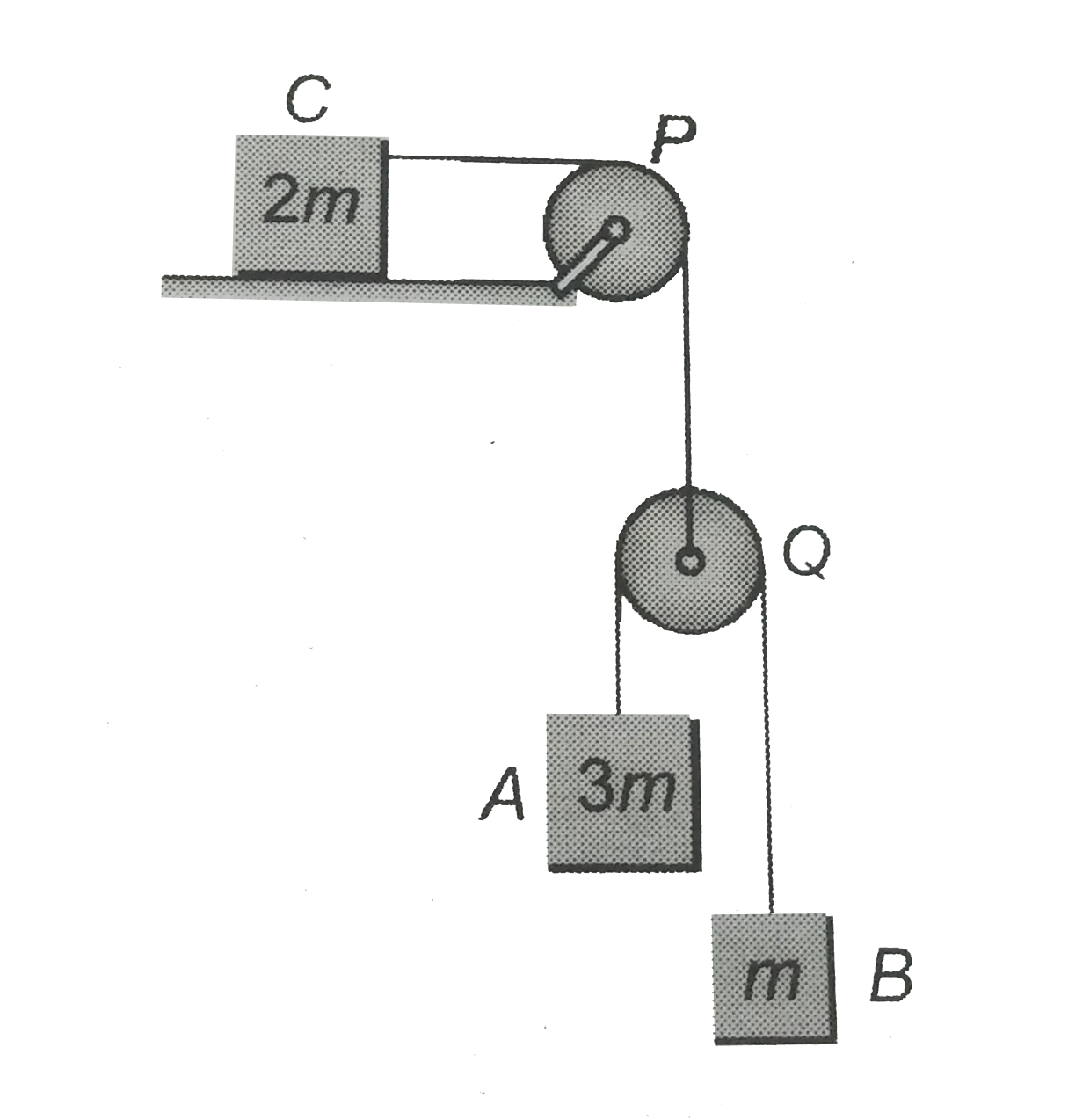
View SolutionIn the arrangement shown in the figure, the blocks have masses 3m,m and 2m, the friction is absent, the masses of the pulleys and the threads are negligible. Find the acceleration of mass 3m.
View Solution

