A rotating disc moves in the positive direction of the x-axis. Find the equation $y (x)$ describing the position of the instantaneous axis of rotation if at the initial moment of the centre $c$ of the disc was located at the point O after which it moved with constant velocity v while the disc started rotating counterclockwise with a constant angular acceleration $a l h p a$ . the initial angular velocity is equal to zero.

Video Solution

Text Solution

Verified by Experts

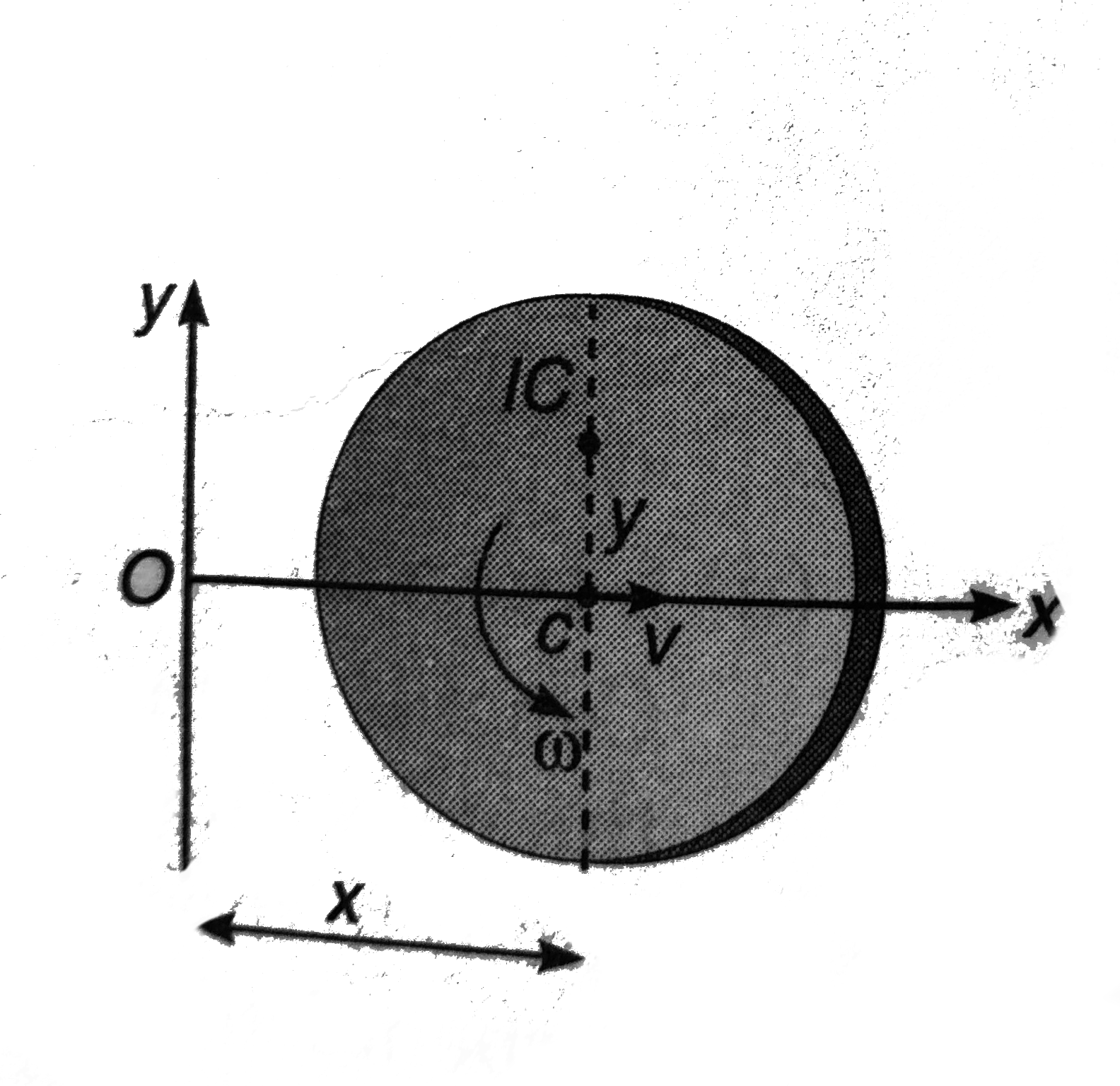
$t = \frac{x}{v}$ and $ω = α t = \frac{α x}{v}$
The positive of IC will be at a distance
$y = \frac{v}{ω}$ or $y = \frac{v}{\frac{α x}{v}}$
or $y = \frac{v^{2}}{α x}$ or $x y = \frac{v^{2}}{α} =$ constant
this is the desired $x . y$ equation. This equation represents a rectangular hyperbola.

Updated on:21/07/2023

Two particles P and Q are located at distance $r_{p} and r_{Q}$ respectively form the centre of rotating disc such that $r_{P} > r_{Q}$ . The disc is rotating with constant angular acceleration. We can say
Aboth P and Q have the same acceleration
Bboth P and Q do not have the same acceleration
CP has greater acceleration than Q
DQ has greater acceleration than P
An ant is sitting at the edge of a rotating disc. If the ant reaches the other end, after moving along the diameter, the angular velocity of the disc will:-
Aremain constant
Bfirst decreases and then increases
Cfirst increases, then decrease
DIincrease continuously
A circular disc is rotating about its own axis at uniform rate completes $30$ rotations in one minute.The angular velocity of disc in rad $s^{- 1}$ is
A $2 π$
B $π$
C $\frac{π}{2}$
D $\frac{π}{4} i$