A non-conducting disc having unifrom positive charge $Q$ , is rotating about its axis with unifrom angular velocity $ω$ .The magnetic field at the centre of the disc is.

directed outward

having magnitude $\frac{μ_{0} Q ω}{4 π R}$

directed inwards

having magnitude $\frac{μ_{0} Q ω}{2 π R}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A, D

Updated on:21/07/2023

a conducting disc of radius $R$ roatates about its axis when an angular velocity $ω$ .Then the potential difference between the centre of the disc and its edge is (no magnetic field is present ):
Azero
B $\frac{m_{e} ω^{2} R^{2}}{2 e}$
C $\frac{m_{e} ω^{2} R^{2}}{3 e}$
D $\frac{e m_{e} ω^{2} R^{2}}{2}$
A conducting disc of radius $r$ spins about its axis an angular velocity $ω$ . There is a uniform magnetic field of magnitude $B$ perpendicular to the plane of the disc $C$ is the centre of the disc.
(i) No emf is induced in the disc
(ii) The potential difference between $C$ and the rim is $1 / 2 B r^{2} ω$
$C$ is at a higher potential than the rim
(iv) Current flows between $C$ and the rim

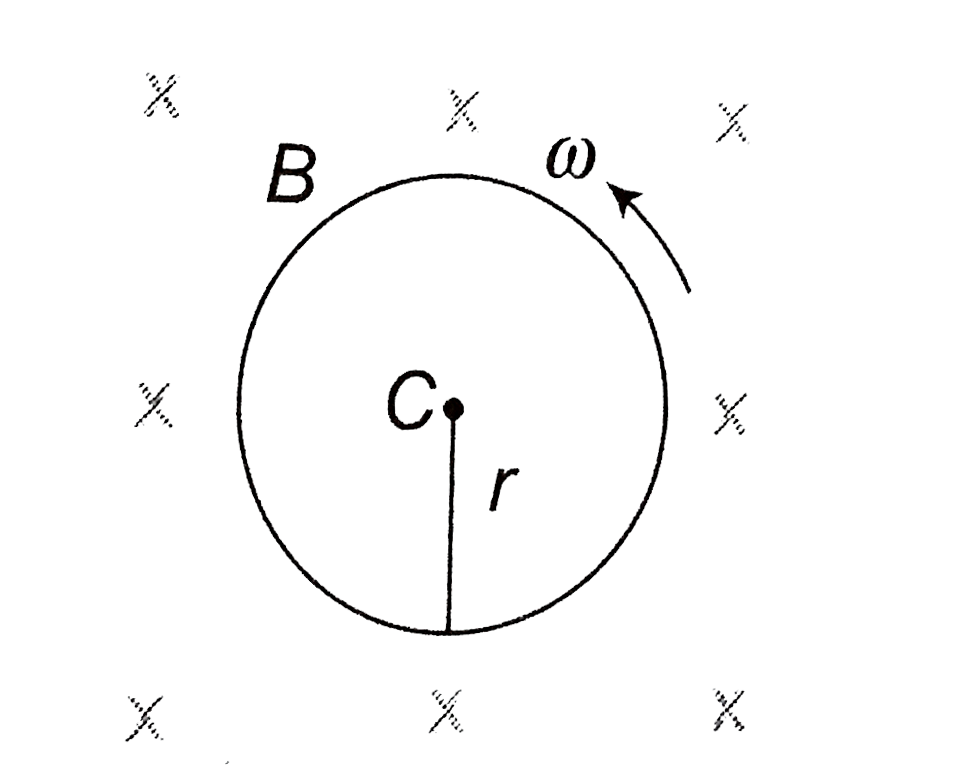A $(i), (i i i)$
B $(i i), (i i i)$
C $(i i), (i v)$
Dnone
A non-conducting disk of radius $R$ is rotating about its own axis with constant angular velocity $ω$ in a perpendicular uniform magnetic field $B$ as shown in figure. The emf induced between centre and rim of disk is

A $\frac{B ω R^{2}}{2}$
B $B ω R^{2}$
CZero
D $\frac{B ω R^{2}}{3}$