A conducting ring of radius r having charge q is rotating with angular velocity ω about its axes. Find the magnetic field at the centre of the ring.

Current in the ring I=ωq2π
Magnetic field B=μ0I2r=μ0ωq(2π)×2r
⇒B=μ0ωq4πr
Topper's Solved these Questions
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICSCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Concept Exercise 2.2
10 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICSCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Exercise (subjective )
10 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICSCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Solved Example
20 Videos
- SEMICONDUCTOR ELECTRONIC : MATERIALS, DEVICES AND SIMPLE CIRCUITSBOOK - CENGAGE PHYSICSCHAPTER - SEMICONDUCTOR ELECTRONIC : MATERIALS, DEVICES AND SIMPLE CIRCUITSEXERCISE - QUESTION BANK
12 Videos
- THERMAL PROPERTIES OF MATTERBOOK - CENGAGE PHYSICSCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Question Bank
40 Videos
Similar Questions
A uniformly charged thin conducting spherical shell of radius R and charge q is rotated with constant angular velocity ω about a diameter. The magnetic dipole moment of the system is
View SolutionA conducting disc of radius r rotates with a small but constant angular velocity ω about its axis. A uniform magnetic field B exists parallel to the axis of rotation. Find the motional emf between the centre and the periphery of the disc.
View Solution
Knowledge Check
A non-conducting disc having unifrom positive charge Q, is rotating about its axis with unifrom angular velocity ω.The magnetic field at the centre of the disc is.
 Adirected outwardBhaving magnitude μ0Qω4πRCdirected inwardsDhaving magnitude μ0Qω2πR
Adirected outwardBhaving magnitude μ0Qω4πRCdirected inwardsDhaving magnitude μ0Qω2πRThere is a ring of radius r having linear charge density λ and rotating with a uniform angular velocity ω. the magnetic field produced by this ring at its own centre would be
Aλω22−μ0Bμ0λ2ω√2Cμ0λω2Dμ0λ2ω2A horizontal ring of radius r spins about its axis with an angular velocity ω in a uniform vertical magnetic field of magnitude B. The emf induced in the ring is
AzeroBπr2ωBC12Br2ωDBr2ω
A ring of mass m and radius R is given a charge q. It is then rotated about its axis with angular velocity ω.Find
(ii) Magnetic field produced at the centre of ring.
View Solution(a) A circular current carrying coil has a radius R. Find magnetic field (a) at centre and (b) along the axis of coil distant √3R from centre. The coil is having N turns and carriers a current i.
(b) Two concentric coil A and B, having current i and 2i and radii 2R and R are placed as shown. Find magnetic field at common centre.
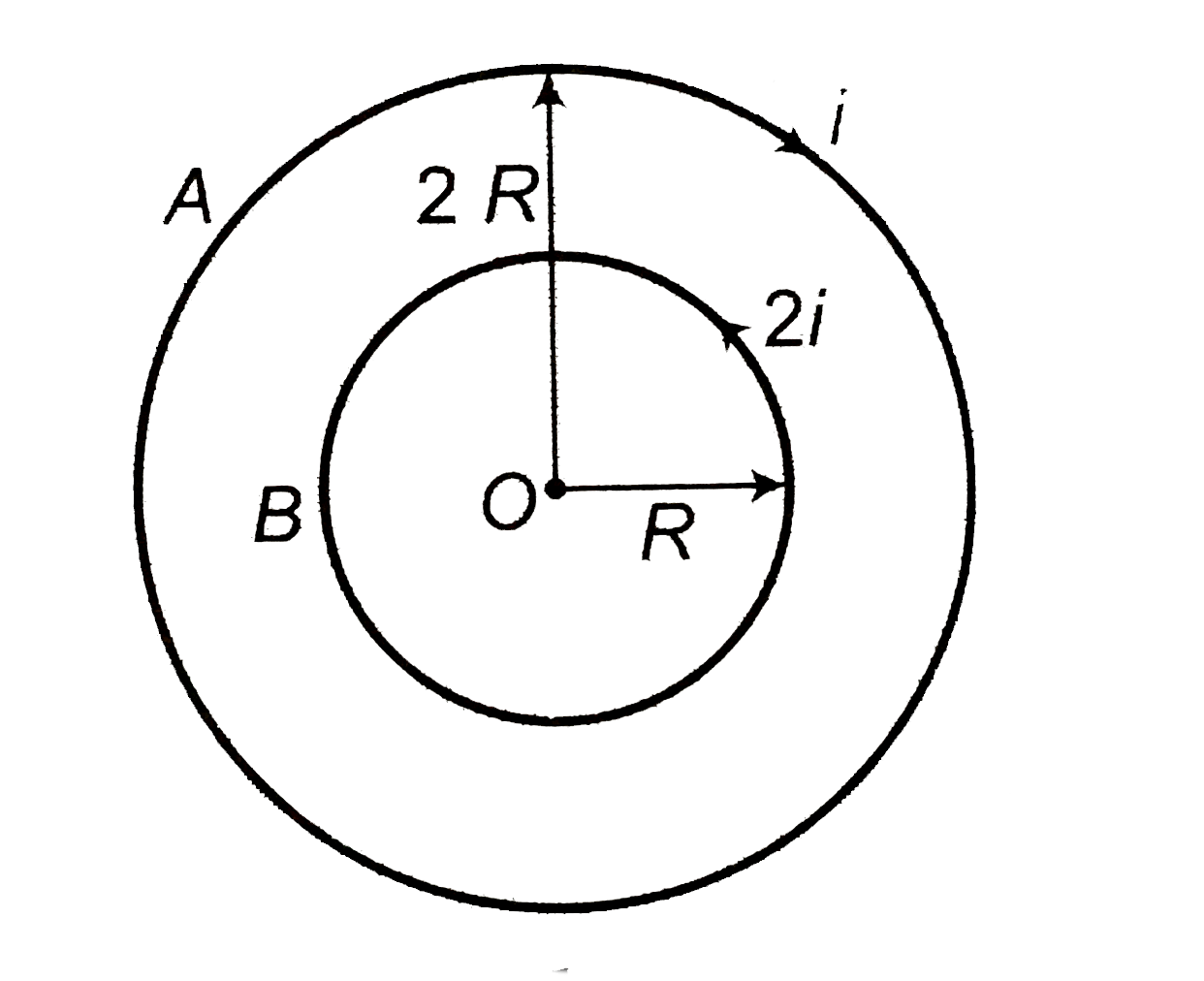
(c) In previous problem, if planes of coil are perpendicular to each other, find magnetic field at common centre.
(d) A charge q distributed uniformely over a circular ring of radius R. The ring rotates about its axis with an angular velocity ω. find the magnetic field (a) at centre and (b) at distance √3R from centre, along the axis.
View SolutionA ring of mass m and radius R is given a charge q. It is then rotated about its axis with angular velocity ω.Find
(iii)Magnetic moment of ring.
View SolutionA non-conducting thin disc of radius R and mass m having charge uniformly over one side with surface density σ rotates about its axis with an angular velocity ω. Find :
(a) the magnetic induction at the centre of the disc,
(b) the magnetic moment of the disc.
( c) the ratio of magnetic moment and angular momentum of disc.
View SolutionA conducting ring of radius R has charge Q distributed unevenly over it. If it rotates with an angular velocity ω, the equivalent current will be
View Solution
