A non-conducting thin disc of radius $R$ and mass $m$ having charge uniformly over one side with surface density $σ$ rotates about its axis with an angular velocity $ω$ . Find :
(a) the magnetic induction at the centre of the disc,
(b) the magnetic moment of the disc.
( c) the ratio of magnetic moment and angular momentum of disc.

Video Solution

Text Solution

Verified by Experts

(a) Consider a ring of radius $x$ and thickness $d x$

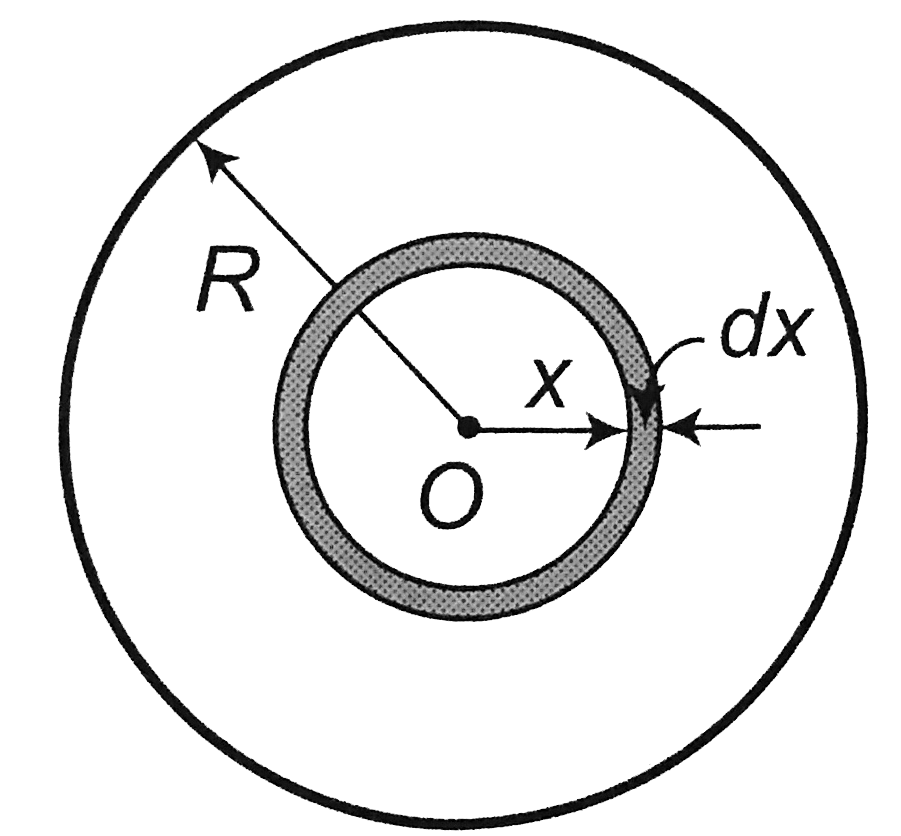
Area $d A = 2 π x d x$
Charge in this area
$d q = σ d A = σ . 2 π x d x$
Current $i = \frac{q}{T} = \frac{σ . 2 π x d x}{2 π / ω}$
$= σ ω x d x$
Magnetic field due to ring
$d B = \frac{μ_{0} i}{2 x} = \frac{μ_{0} σ ω x d x}{2 x}$
$B_{0} = \frac{μ_{0} σ ω}{2} \int_{0}^{R} d x = \frac{μ_{0} σ ω R}{2}$
(b) Magnetic moment of ring
$d M = i . π x^{2}$
$M = σ ω π \int_{0}^{R} x^{3} d x$
$= \frac{σ ω π R^{4}}{4}$
( c) Angular momentum of disc
$L = I ω = \frac{1}{2} m R^{2} ω, I : M . I$ . of disc about its axis
$\frac{M}{L} = \frac{σ ω π R^{4} / 4}{m R^{2} ω / 2} = \frac{1}{2} \frac{σ π R^{2}}{m} = \frac{q}{2 m}$
where $q (= σ . π R^{2})$ : total charge on disc.

Updated on:21/07/2023

A thin disc of radius R has charge Q distributed uniformly on its surface. The disc is rotated about one of its diametric axis with angular velocity $ω$ . The magnetic moment of the arrangement is
A $\frac{Q R^{2} ω}{8}$
B $\frac{Q R^{2} ω}{4}$
C $\frac{Q R^{2} ω}{2}$
DZero
A non-conducting disc having unifrom positive charge $Q$ , is rotating about its axis with unifrom angular velocity $ω$ .The magnetic field at the centre of the disc is.

Adirected outward
Bhaving magnitude $\frac{μ_{0} Q ω}{4 π R}$
Cdirected inwards
Dhaving magnitude $\frac{μ_{0} Q ω}{2 π R}$
A thin annular disc of outer radius R and $\frac{R}{2}$ inner radius has charge Q uniformly distributed over its surface. The disc rotates about its axis with a constant angular velocity $ω$ . Choose the correct option(s):
AThe magnetic field intensity at the centre of the disc is $\frac{μ_{0} Q ω}{3 π R}$
BThe magnetic field intensity at the centre of the disc is $\frac{μ_{0} Q ω}{4 R}$
CThe magnetic moment of the disc is $\frac{5 Q ω R^{2}}{16}$
DThe magnetic moment of the disc is $\frac{3 Q ω R^{2}}{4}$