The magnetic field at the origin due to a current element I→dl placed at position r is
(i) (μ0i4π)(d→l×→rr3)
−(μ0i4π)(d→l×→rr3)
(iii) (μ0i4π)(→r×d→lr3)
−(μ0i4π)(→r×d→lr3)
(i),(ii)
(ii),(iii)
(i),(ii)
(iii),(iv)
The correct Answer is:B
To solve the problem, we will use the Biot-Savart Law, which describes the magnetic field generated by a current-carrying conductor.
1. Understanding the Biot-Savart Law:
The Biot-Savart Law states that the magnetic field →B at a point in space due to a current element I→dl is given by:
d→B=μ0I4πd→l×→rr3
where →r is the position vector from the current element to the point where the magnetic field is being calculated, and r is the magnitude of →r.
2. Positioning the Current Element:
In this scenario, the current element I→dl is located at position →r and we want to find the magnetic field at the origin.
3. Applying the Biot-Savart Law:
Since we are calculating the magnetic field at the origin due to the current element at position →r, we can substitute into the Biot-Savart Law:
d→B=μ0I4πd→l×→rr3
4. Considering the Direction:
The direction of the magnetic field due to a current element follows the right-hand rule. The vector d→l is in the direction of the current, and →r points from the current element to the origin.
5. Evaluating the Options:
- Option (i): μ0I4πd→l×→rr3 is incorrect because it does not account for the direction of the magnetic field correctly.
- Option (ii): −μ0I4πd→l×→rr3 is correct as it includes the negative sign indicating the direction of the magnetic field.
- Option (iii): μ0I4π→r×d→lr3 is also correct because →r×d→l=−d→l×→r (due to the properties of the cross product).
6. Conclusion:
Therefore, the correct options are (ii) and (iii).
Final Answer:
The correct options are (ii) and (iii).
The Biot-Savart Law states that the magnetic field →B at a point in space due to a current element I→dl is given by:
d→B=μ0I4πd→l×→rr3
where →r is the position vector from the current element to the point where the magnetic field is being calculated, and r is the magnitude of →r.
In this scenario, the current element I→dl is located at position →r and we want to find the magnetic field at the origin.
Since we are calculating the magnetic field at the origin due to the current element at position →r, we can substitute into the Biot-Savart Law:
d→B=μ0I4πd→l×→rr3
The direction of the magnetic field due to a current element follows the right-hand rule. The vector d→l is in the direction of the current, and →r points from the current element to the origin.
- Option (i): μ0I4πd→l×→rr3 is incorrect because it does not account for the direction of the magnetic field correctly.
- Option (ii): −μ0I4πd→l×→rr3 is correct as it includes the negative sign indicating the direction of the magnetic field.
- Option (iii): μ0I4π→r×d→lr3 is also correct because →r×d→l=−d→l×→r (due to the properties of the cross product).
Therefore, the correct options are (ii) and (iii).
The correct options are (ii) and (iii).
Topper's Solved these Questions
Similar Questions
Knowledge Check
The magnetic field ¯¯¯¯¯dB due to a small current element ¯¯¯dl at a distance →r and carrying current 'I' is
A¯¯¯¯¯dB=μ04πi(¯¯¯dlׯrr)B¯¯¯¯¯dB=μ04πi2(¯¯¯dlׯrr2)C¯¯¯¯¯dB=μ04πi2(¯¯¯dlׯrr)D¯¯¯¯¯dB=μ04πi(¯¯¯dlׯrr3)The magnetic induction at centre of loop due to current flowing through small element 'dl' is given as dB=μ04πIdlsinθr2 where θ is
A0∘B180∘C90∘D60∘The lines →r=→a+λ(→b×→c)&→r=→b+μ(→c×→a) will intersect, if
A→a×→c=→b×→cB→a.→c=→b.→cC→b×→a=→c×→aDNone
The earth may be considered to be a big dipole of moment 6.4×1012Am placed at its centre with its axis in the SN direction. The radius of the earth is 6000 km. Calculate the horizontal and vertical components of the earth's magnetic field at a place whose lattitude is 22∘N.
[Hint: Br=μ04π2mcosθr3 and Bθ=μ04πmsinθr3, here θ=90∘+22∘=112∘]
View SolutionThe vector form of Coulomb's law is (A) →F=14πε0⋅q1q2|→r|3→r (B) →F=14πε0⋅q1q2r3 (C) →F=14πε0⋅q1q2r2→r (D) →F=14πε0⋅q1q2r→r
View Solution→r=2tˆi+3t→2ˆj. Find →v and →a where →v=d→rdr,→a=d→vdt
View SolutionIn the given loop the magnetic field at the centre O is
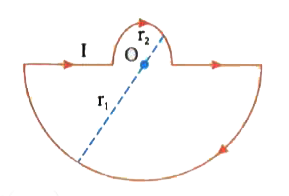
1) μ0I4(r1+r2r1r2) out of the page
2) μ0I4(r1+r2r1r2) into the page
3) μ0I4(r1−r2r1r2) out of the page
4) μ0I4(r1−r2r1r2) into the page
View SolutionGiven R(r)=19√3(14π)1/2(1a0)3/2(6−4ra0+49r2a20)e.r3a0
Which in INCORRECT statement about R(r ).
View Solution
