A thin annular disc of outer radius R and R2 inner radius has charge Q uniformly distributed over its surface. The disc rotates about its axis with a constant angular velocity ω. Choose the correct option(s):
The magnetic field intensity at the centre of the disc is μ0Qω3πR
The magnetic field intensity at the centre of the disc is μ0Qω4R
The magnetic moment of the disc is 5QωR216
The magnetic moment of the disc is 3QωR24
The correct Answer is:A, C
To solve the problem of a thin annular disc with outer radius R and inner radius R2 that rotates with a constant angular velocity ω and has a uniformly distributed charge Q, we will follow these steps:
Step 1: Calculate the Surface Charge Density
The surface charge density σ is given by the total charge Q divided by the area of the annular disc.
The area A of the annular disc is:
A=πR2−π(R2)2=πR2−πR24=3πR24
Thus, the surface charge density σ is:
σ=QA=Q3πR24=4Q3πR2
Step 2: Determine the Current Element
Consider a small ring element of radius r and thickness dr. The area dA of this ring is:
dA=2πrdr
The charge dq on this ring is:
dq=σdA=σ⋅2πrdr=4Q3πR2⋅2πrdr=8Q3R2rdr
Step 3: Calculate the Current di
The current di due to the rotating charge is given by:
di=dqT
where T is the period of rotation. The period T can be expressed in terms of angular velocity ω:
T=2πω
Thus,
di=dqT=8Q3R2rdr⋅ω2π=4Qω3πR2rdr
Step 4: Calculate the Magnetic Field at the Center
The magnetic field dB at the center of the disc due to the current element di is given by:
dB=μ0di2r
Substituting di:
dB=μ02r⋅4Qω3πR2rdr=2μ0Qω3πR2dr
To find the total magnetic field B at the center, integrate dB from r=R2 to r=R:
B=∫RR/2dB=∫RR/22μ0Qω3πR2dr=2μ0Qω3πR2(R−R2)=2μ0Qω3πR2⋅R2
B=μ0Qω3πR
Step 5: Calculate the Magnetic Moment
The magnetic moment m of the disc is given by:
m=Number of turns×Current×Area
For our case, the area of the annular disc is A=3πR24, and the current I is given by integrating di:
m=1⋅∫RR/2di⋅3πR24
Substituting di:
m=3πR24⋅∫RR/24Qω3πR2rdr=3πR24⋅4Qω3πR2⋅(r22)RR/2
=3πR24⋅4Qω3πR2⋅(R22−(R/2)22)=3πR24⋅4Qω3πR2⋅(R22−R28)
=3πR24⋅4Qω3πR2⋅3R28=QωR28
Conclusion
The magnetic field intensity at the center of the disc is:
B=μ0Qω3πR
And the magnetic moment of the disc is:
m=5QωR216
The surface charge density σ is given by the total charge Q divided by the area of the annular disc.
A=πR2−π(R2)2=πR2−πR24=3πR24
σ=QA=Q3πR24=4Q3πR2
Consider a small ring element of radius r and thickness dr. The area dA of this ring is:
dA=2πrdr
dq=σdA=σ⋅2πrdr=4Q3πR2⋅2πrdr=8Q3R2rdr
The current di due to the rotating charge is given by:
di=dqT
where T is the period of rotation. The period T can be expressed in terms of angular velocity ω:
T=2πω
di=dqT=8Q3R2rdr⋅ω2π=4Qω3πR2rdr
The magnetic field dB at the center of the disc due to the current element di is given by:
dB=μ0di2r
dB=μ02r⋅4Qω3πR2rdr=2μ0Qω3πR2dr
B=∫RR/2dB=∫RR/22μ0Qω3πR2dr=2μ0Qω3πR2(R−R2)=2μ0Qω3πR2⋅R2
B=μ0Qω3πR
The magnetic moment m of the disc is given by:
m=Number of turns×Current×Area
m=1⋅∫RR/2di⋅3πR24
m=3πR24⋅∫RR/24Qω3πR2rdr=3πR24⋅4Qω3πR2⋅(r22)RR/2
=3πR24⋅4Qω3πR2⋅(R22−(R/2)22)=3πR24⋅4Qω3πR2⋅(R22−R28)
=3πR24⋅4Qω3πR2⋅3R28=QωR28
The magnetic field intensity at the center of the disc is:
B=μ0Qω3πR
And the magnetic moment of the disc is:
m=5QωR216
Similar Questions
Calculate potential on the axis of a disc of radius R due to a charge Q uniformly distributed on its surface.
View SolutionA non-conducting thin disc of radius R and mass m having charge uniformly over one side with surface density σ rotates about its axis with an angular velocity ω. Find :
(a) the magnetic induction at the centre of the disc,
(b) the magnetic moment of the disc.
( c) the ratio of magnetic moment and angular momentum of disc.
View Solution
Knowledge Check
A disc of mass m has a charge Q distributed on its surface. It is rotating about an XX' with a angular velocity ω. The force acting on the disc is
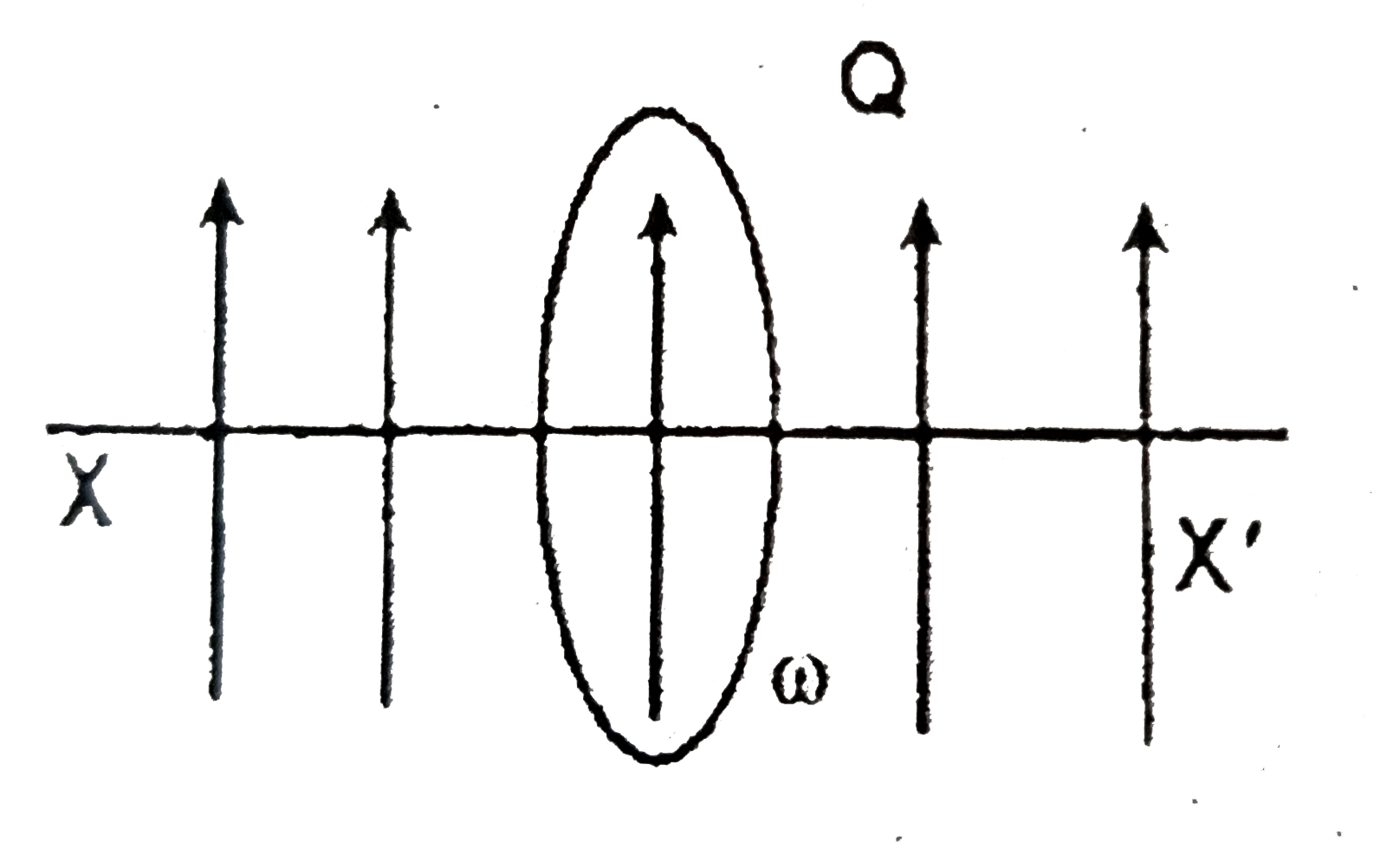 AzeroBωRB/πC2QωBRDnone of these
AzeroBωRB/πC2QωBRDnone of theseA thin disc of radius R has charge Q distributed uniformly on its surface. The disc is rotated about one of its diametric axis with angular velocity ω. The magnetic moment of the arrangement is
AQR2ω8BQR2ω4CQR2ω2DZeroA long, hollow insulating cylinder of radius R and negligible thickness has a uniform surface charge density σ. The cylinder rotates about its central axis at a constant angular speed ω. Choose the correct option(s):
AThe charge crossing an imaginary line of length L on the surface of the cylinder, parallel to its axis, per unit time, is ωσRL.BThe magnetic moment of a length L of the cylinder is πωσR3LCThe magnetic field intensity at a point on the axis of the cylinder, inside the cylinder, is μ0ωσR2DIf the direction of rotation of the cylinder is reversed, the magnetic field at a point on the axis of the cylinder will also reverse direction
A plastic disc of radius 'R' has a charge 'q' uniformly distributed over its surface. If the dis is rotated with a frequency 'f' about its axis, then the magnetic induction at the centre of the disc is given by
View SolutionA non-conducting thin disc of radius R charged uniformly over one side with surface density s rotates about its axis with an angular velocity ω. Find
(a) the magnetic induction at the centre of the disc,
(b) the magnetic moment of the disc.
View SolutionA hollow sphere has charge 'q' which is uniformly distributed over its surface and rotating about its axis .Find the magnetic moment of the sphere
View SolutionA hollow non conducting sphere of radius R has a positive charge q uniformly distributed on its surface. The sphere starts rotating with a constant angular velocity 'ω' about an axis passing through center of sphere, as shown in the figure. Then the net magnetic field at center of the sphere is

View SolutionA thin disc of radius R and mass M has charge q uniformly distributed on it. It rotates with angular velocity ω. The ratio of magnetic moment and angular momentum for the disc is
View Solution
