a conducting disc of radius R roatates about its axis when an angular

A metal disc of radius a rotates with a constant angular velocity $ω$ about its axis. The potential difference between the center and the rim of the disc is $(m = mass of electron, e = charge on electro)$
A $\frac{m ω^{2} a^{2}}{e}$
B $\frac{1}{2} \frac{m ω^{2} a^{2}}{e}$
C( c) $\frac{e ω^{2} a^{2}}{2 m}$
D $\frac{e ω^{2} a^{2}}{m}$
A non-conducting disc having unifrom positive charge $Q$ , is rotating about its axis with unifrom angular velocity $ω$ .The magnetic field at the centre of the disc is.

Adirected outward
Bhaving magnitude $\frac{μ_{0} Q ω}{4 π R}$
Cdirected inwards
Dhaving magnitude $\frac{μ_{0} Q ω}{2 π R}$
A conducting disc of radius $r$ spins about its axis an angular velocity $ω$ . There is a uniform magnetic field of magnitude $B$ perpendicular to the plane of the disc $C$ is the centre of the disc.
(i) No emf is induced in the disc
(ii) The potential difference between $C$ and the rim is $1 / 2 B r^{2} ω$
$C$ is at a higher potential than the rim
(iv) Current flows between $C$ and the rim

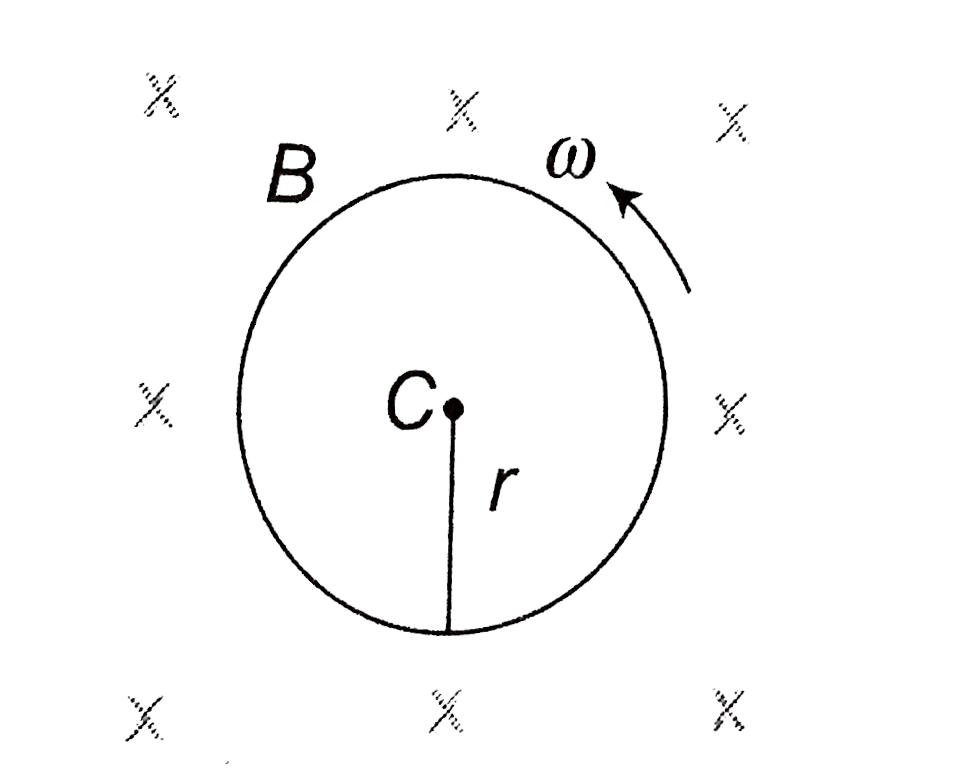A $(i), (i i i)$
B $(i i), (i i i)$
C $(i i), (i v)$
Dnone

a conducting disc of radius $R$ roatates about its axis when an angular velocity $ω$ .Then the potential difference between the centre of the disc and its edge is (no magnetic field is present ):