A uniform solid cylinder of mass $m$ and radius $R$ is set in rotation about its axis with an angular velocity $ω_{0}$ , then lowered with its lateral surface onto a horizontal plane and released. The coefficient of friction between the cylinder and the plane is equal to $μ$ . Find
( $a$ ) how long the cylinder will move with sliding,
( $b$ ) the total work performed by the sliding friction force acting on the cylinder.

Video Solution

Text Solution

Verified by Experts

(a) Let us depict the forces acting on the cylinder and their point of applications for the cylinder and indicate positive direction of $x$ and $φ$ as shown in the figure. From the equations for the plane motion of a solid $F_{x} = m w_{c x}$ and $N_{c z} = I_{c} β_{z}$ :
$k m g = m w_{c x}$ or $w_{c x} = k g$ (1)
$- k m g R = \frac{m R^{2}}{2} β^{z}$ or $β_{z} = - 2 \frac{k g}{R}$ (2)
Let the cylinder starts pure rolling at $t = t_{0}$ after releasing on the horizontal floor at $t = 0$ . From the angular kinematical equation.
$ω_{z} = ω_{o z} + β_{z} t$ ,
or $ω = ω_{0} - 2 \frac{k g}{R} t$ (3)
From the equation of the linear kinematics,
$v_{c x} = v_{0 c x} + w_{c x} t$
or $v_{c} = 0 + k g t_{0}$ (4)
But at the moment $t = t_{0}$ , when pure rolling starts $v_{c} = ω R$
so, $k g t_{0} = (ω_{0} - 2 \frac{k g}{R} t_{0}) R$
Thus $t_{0} = \frac{ω_{0} R}{3 k g}$

(b) As the cylinder pick, up speed till it starts rolling, the point of contact has a purely translatory movement equal to $\frac{1}{2} w_{c} t_{0}^{2}$ in the forward directions but there is also a backward movment of the point of contant of magnitude $(ω_{0} τ_{0} - \frac{1}{2} β t_{0}^{2}) R$ . Because of slipping the net displacement is backwards. The total work done is then,
$A_{f r} = k m g [\frac{1}{2} w_{c} t_{0}^{2} - (ω_{0} t_{0} + \frac{1}{2} β t_{0}^{2}) R]$
$= k m g [\frac{1}{2} k g t_{0}^{2} - \frac{1}{2} (- \frac{2 k g}{R}) t_{0}^{2} R - ω_{0} t_{0} R]$
$= (k m g) \frac{ω_{0} R}{3 k g} [\frac{ω_{0} R}{6} + \frac{ω_{0} R}{3} - ω_{0} R] = - \frac{m ω_{0}^{2} R^{2}}{6}$
The same result can also be obtained by the work-energy theorem, $A_{f r} = Δ T$ .

Updated on:21/07/2023

A solid cylinder of mass M and radius R rotates about its axis with angular speed $ω$ . Its rotational kinetic energy is
A $\frac{1}{2} M R^{2} ω^{2}$
B $M R^{2} ω^{2}$
C $\frac{1}{4} M R^{2} ω^{2}$
D $\frac{1}{8} M R^{2} ω^{2}$
An cylinder of mass $m$ is rotated about its axis by an angular velocity $ω$ and lowered gently on an inclined plane as shown in figure. Then :
.
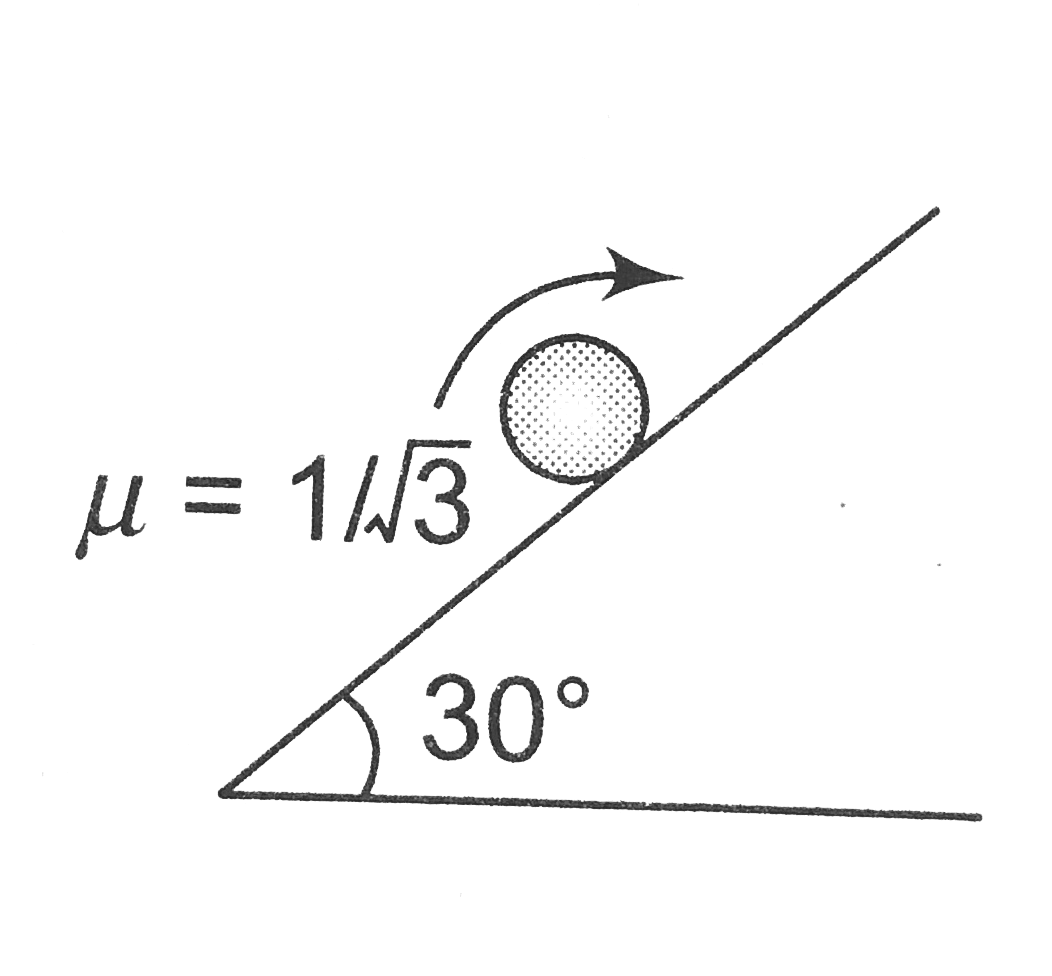Ait will start going upward
Bit will first going upward and then downward
Cit will go downward just after it is lowered
Dit can never go upward.
A uniform circular ring of radius $R$ is first rotated about its horizontal axis with an angular velocity $ω_{0}$ and then carefully placed on a rough horizontal surface as shown. The coefficient of friction between the surface and the rings $μ$ . Time after which its angular speed is reduced to $0.5 ω_{0}$ is

A $\frac{ω_{0} μ R}{2 g}$
B $\frac{ω_{0} g}{2 μ R}$
C $\frac{2 ω_{0} R}{μ g}$
D $\frac{ω_{0} R}{2 μ g}$