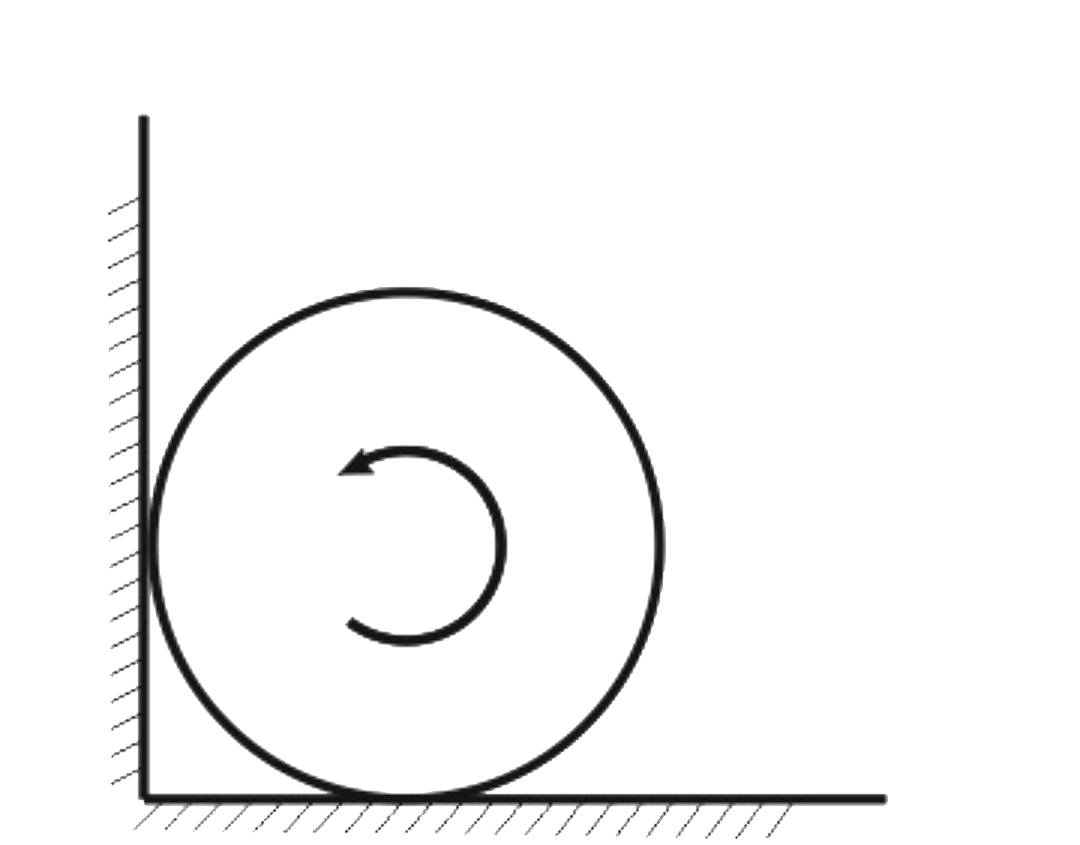
A uniform cylinder of radius R is spinned about it axis to the angular velocity ω0 and then placed into a corner,. The coeficient of friction between the corner walls and the cylinder is μk How many turns will the cylinder accomplish before it stops?


ΣFx=0,N1−μkN−1=0……….i
ΣFy=0,N1+μkN2−mg=0……..ii
Solving these equations N1=m1+μ2k:N2=μkmg1+μk2
The torque on the cylinder about the axis of rotation
τCM=mg×0+N1×0+N2×0+μkN2R
=μk(1+μk)(1+μ2k)mgR
The moment of inertia about axis of rotation ICM=12mR2
The torque equation τ=Iα
μk(1+μk)(1+μ2k)mgR=(12mR2)α⇒=2μk(1+μk)g(1+μ2k)R
Using equation ω2=ω20+2aθ, calculate the angular displacement θ.
02=ω20−2[2μk(1+μk)g(1+μ2k)R]θ
(ω and α are in the opposite sense)
⇒θ=(1+μ2k)ω20R(4μ+k(1+μk)g)
Revolution accomplished
n=θ2π=(1+μ2k)ω20R2π×4μk(1+μk)g=(1+μ2k)ω20R8πμk(1+μk)g
Topper's Solved these Questions
- RIGID BODY DYNAMICS 1Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 1Exercise:Solved Examples
Explore 9 Videos
- RIGID BODY DYNAMICS 1Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 1Exercise:Exercise 2.1
Explore 6 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBook:CENGAGE PHYSICSChapter:PROPERTIES OF SOLIDS AND FLUIDSExercise:INTEGER_TYPE
Explore 2 Videos
- RIGID BODY DYNAMICS 2Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 2Exercise:Interger
Explore 2 Videos
Similar Questions
A uniform cylinder of the radius R ( = 3 m) is spin about its axis at an angular velocity ω0(=40√π rad s−1) and placed between two perpendicular walls. The coefficient of friction between the walls and cylinder is μ(=2). Then, how many rotations will the cylinder make before it comes to rest?
View SolutionA uniform solid cylinder of mass m and radius R is set in rotation about its axis with an angular velocity ω0, then lowered with its lateral surface onto a horizontal plane and released. The coefficient of friction between the cylinder and the plane is equal to μ. Find
(a) how long the cylinder will move with sliding,
(b) the total work performed by the sliding friction force acting on the cylinder.
View Solution
Knowledge Check
A uniform circular ring of radius R is first rotated about its horizontal axis with an angular velocity ω0 and then carefully placed on a rough horizontal surface as shown. The coefficient of friction between the surface and the rings μ. Time after which its angular speed is reduced to 0.5ω0 is
 Aω0μR2gBω0g2μRC2ω0RμgDω0R2μg
Aω0μR2gBω0g2μRC2ω0RμgDω0R2μgAn cylinder of mass m is rotated about its axis by an angular velocity ω and lowered gently on an inclined plane as shown in figure. Then :
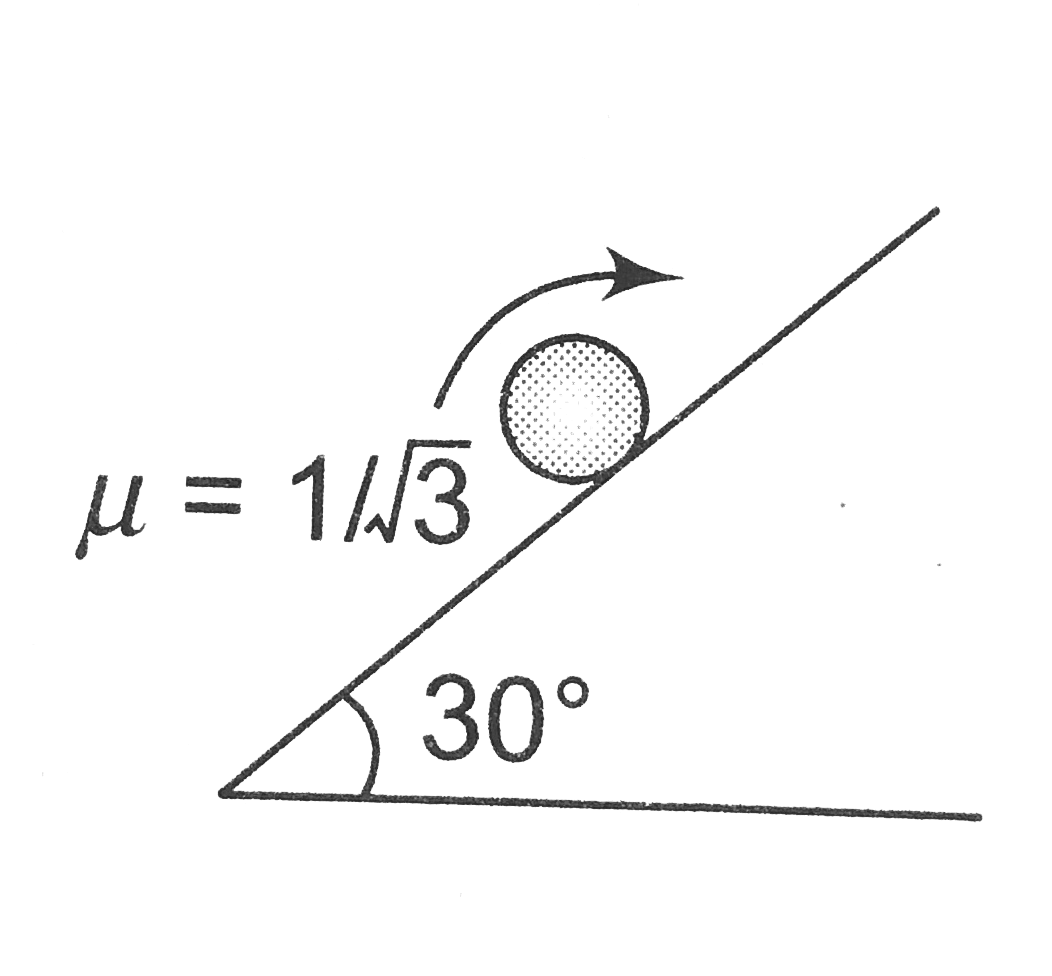 .Ait will start going upwardBit will first going upward and then downwardCit will go downward just after it is loweredDit can never go upward.
.Ait will start going upwardBit will first going upward and then downwardCit will go downward just after it is loweredDit can never go upward.A uniform cylinder of mass M and radius R is placed on a rough horizontal board, which in turn is placed on a smooth surface. The coefficient of friction between the board and the cylinder is μ. If the board starts accelerating with constant acceleration a, as shown in the figure, then
 Afor pure rolling motion of the cylinder, direction of frictional force is forward and its magnitude is Ma/3Bthe maximum value of a, so that cyliner performs pure rolling is 3μgCThe acceleration of the centre of mass of te cylinder under pure rolling condition for the given a is a/3Dnone of these
Afor pure rolling motion of the cylinder, direction of frictional force is forward and its magnitude is Ma/3Bthe maximum value of a, so that cyliner performs pure rolling is 3μgCThe acceleration of the centre of mass of te cylinder under pure rolling condition for the given a is a/3Dnone of these
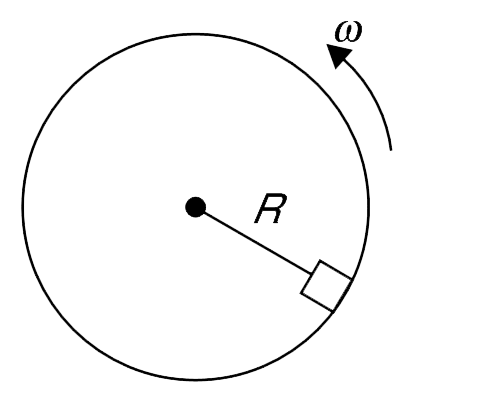
A cylinder with radius R spins about its horizontal axis with angular speed ω. There is a small block lying on the inner surface of the cylinder. The coefficient of friction between the block and the cylinder is μ. Find the value of ω for which the block does not slip, i.e., stays at rest with respect to the cylinder.
View SolutionA cylinder full of water is rotating about its own axis with uniform angular velocity ω. Then the shape of free surface of water will be
View SolutionA cylinder of mass m radius R is spined to a clockwise angular velocity ωo and then gently placed on an inclined plane for which coefficient of friction μ=tanθ,θ is the angle of inclined plane with the horizontal. The centre of mass of cylinder will remain stationary for time

View SolutionA horizontal ring of radius r spins about its axis with an angular velocity ω in a uniform vertical magnetic field of magnitude B. The emf induced in the ring is
View SolutionA solid cylinder of mass m and radius r is rolling on a rough inclined plane of inclination θ. The coefficient of friction between the cylinder and incline is μ. Then.
View Solution

