A uniform solid cylinder of mass m rests on two horizontal planks. A thread is wound on the cylinder. The hanging end of the thread is pulled vertically down with a constant force F(figure).
Find the maximum magnitude of the force F which still does not bring about any sliding of the cylinder, if the coefficient of friction between the cylinder and the planks is equal to k. What is the acceleration wmax of the axis of the cylinder rolling down the inclined plane?

Let us sketch the force diagram for solid cylinder and apply Newton's second law in projection form along x and y axes (figure):
fr1+fr2=mwc (1)
and N1+N2−mg−F=0
or N1+N2=mg+F (2)
Now choosing positive direction of φ as shown in the figure and using Ncz=Icβz,
we get
FR−(fr1+fr2)R=mR22β=mR22wcR (3)
[as for pure rolling wc=βR]. In addition to,
fr1+fr2≤k(N1+N2) (4)
Solving the Eqs., we get
F≤3kmg(2−3k), or Fmax=3kmg2−3k
and wc(max)=k(N1+N2)m
=km[mg+Fmax]=km[mg+3kmg2−3k]=2kg2−3k

Topper's Solved these Questions
- PHYSICAL FUNDAMENTALS OF MECHANICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:PHYSICAL FUNDAMENTALS OF MECHANICSExercise:Elastic Deformation Of Asolid Body
Explore 25 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:PHYSICAL FUNDAMENTALS OF MECHANICSExercise:Hydrodynamics
Explore 25 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:PHYSICAL FUNDAMENTALS OF MECHANICSExercise:Universal Gravitation
Explore 34 Videos
- OSCILLATIONS AND WAVESBook:IE IRODOV, LA SENA & SS KROTOVChapter:OSCILLATIONS AND WAVESExercise:Electromagnetic Waves, Radiation
Explore 36 Videos
- THERMODYNAMICS AND MOLECULAR PHYSICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:THERMODYNAMICS AND MOLECULAR PHYSICSExercise:Transport Phenomena
Explore 38 Videos
Similar Questions
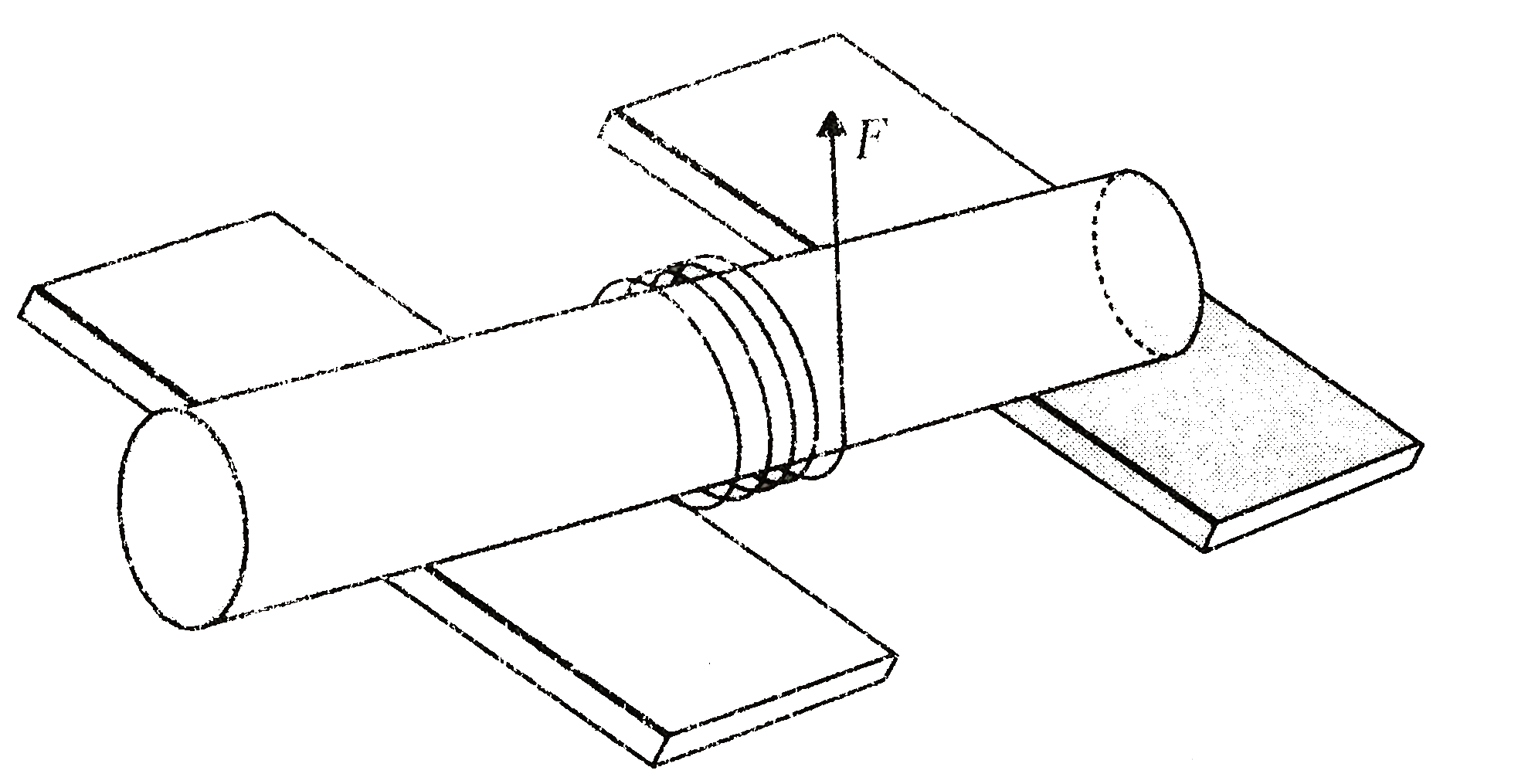
A uniform solid cylinder of mass m rests on two horizontal planks as shown in Fig. A thread is wound on the cylinder. The hanging end of the thread is pulled vertically up with a force F. What is the maximum magnitude of the force F which still does not bring about any sliding of the cylinder, if the coefficient of friction between the cylinder and the planks is equal to μ. What is the maximum acceleration of the axis of the cylinder?
View SolutionA uniform solid cylinder of mass m rests on two horizontal planks. A thread is wound on the cylinder. The hanging end of the thread is pulled vertically down with a constant force F.
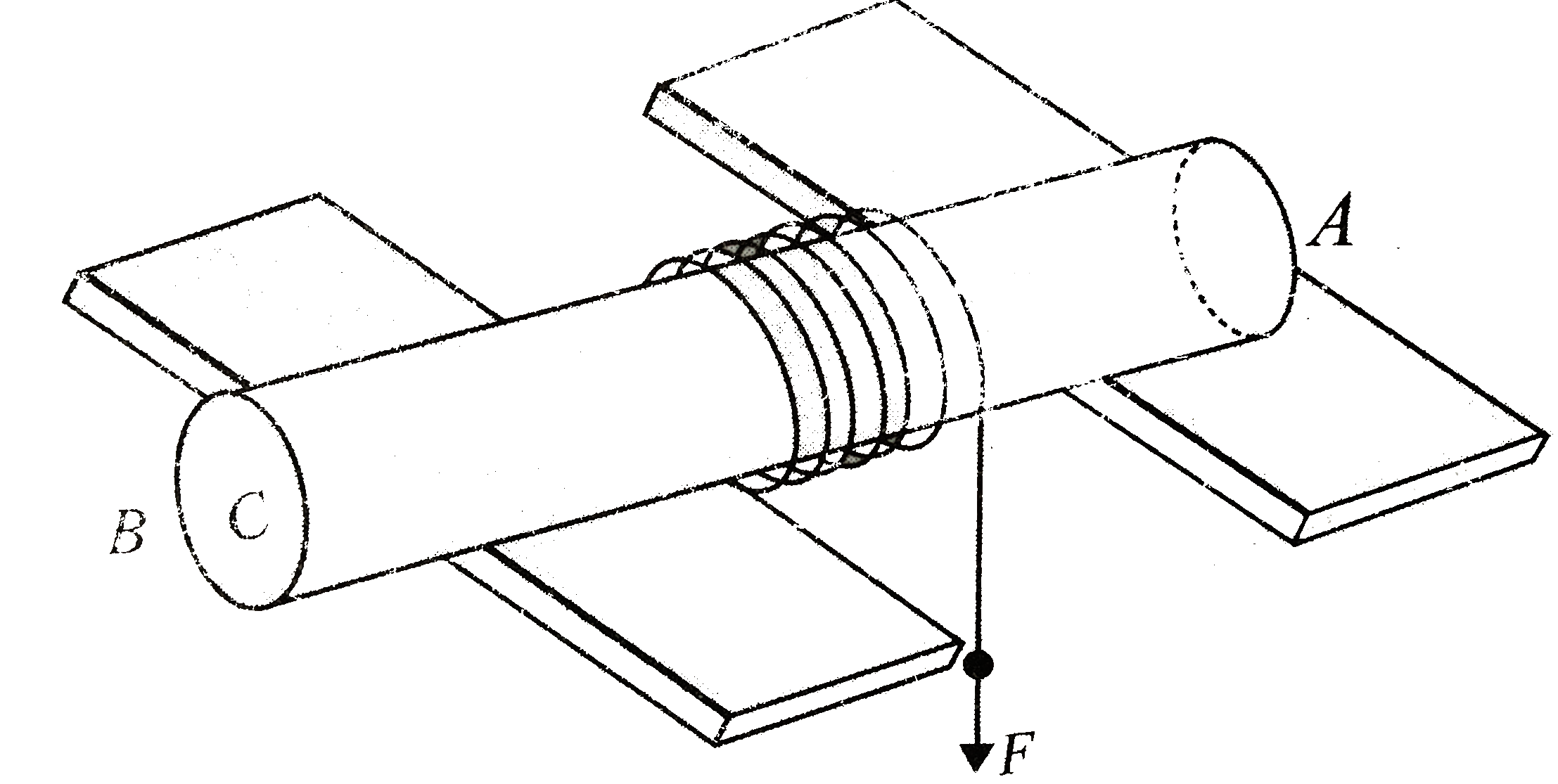
Find the maximum magnitude of the force F which may be applied without bringing about any sliding of the cylinder, if the coefficient of friction between the plank and the cylinder is equal to μ. What is the maximum acceleration of the centre of mass over the planks?
View Solution
Knowledge Check
A uniform cylinder of mass m rests on two rough horizontal planks. A thread is wound on the cylinder. The hanging end of the thread is pulled vertically down with a constant force F
ASince horizontal acceleration is provided by the friction acting on the cylinder, its translation kinetic energy (12mv2) is equal to work done by this friction,BSince moment about instantaneous axis of rotation is produced by force F. kinetic energy (12Iω2) is equal to work done by F where I is moment of inertia about the instantaneous axis of rotation and ω is the-angular velocity.CSince cylinder is moving, energy is lost against friction.DWork done by F+ work done by friction on cylinder =totalKE of the cylinder.
A uniform solid cylinder having mass M and radius R is pulled by a horiozntal force F acting through the center as shown. The cylinder rolls to the right without slipping. What is the magnitude of the force of friction between the cylinder and the ground?AF/4BF/3CF/2D2F/3
A uniform solid cylinder of mass m and radius R is placed on a rough horizontal surface. A horizontal constant force F is applied at the top point P of the cylinder so that it start pure rolling. The acceleration of the cylinder isAF/3mB2F/3mC4F/3mD5F/3m
A solid cylinder of mass 8 kg is rolling perfectly down an inclined plane of inclination 30. Calculate the force of friction between the cylinder and inclined plane and acceleration of the cylinder down the inclined plane.
View SolutionLight thread is tightly wound on a uniform solid cylinder of radius R. The cylinder is placed on a smooth horizontal table and the thread is pulled horizontally as shown, by applying a constant force F. How much length of the thread is unwound from the cylinder by the time its kinetic energy becomes equal to K.
View SolutionA solid cylinder of mass m is resting on fixed rough inclined plane with help of a thread. Find friction force between cylinder and inclined plane. (given μ=0.4)

View SolutionA uniform solid. cylinder A of mass can freely rotate about a horizontal axis fixed to a mount of mass m2. A constant horizontal force F is applied to the end K of a light thread tightly wound on the cylinder. The friction between the mount and the supporting horizontal plane is assumed to be absent. Find the acceleration of the point K.
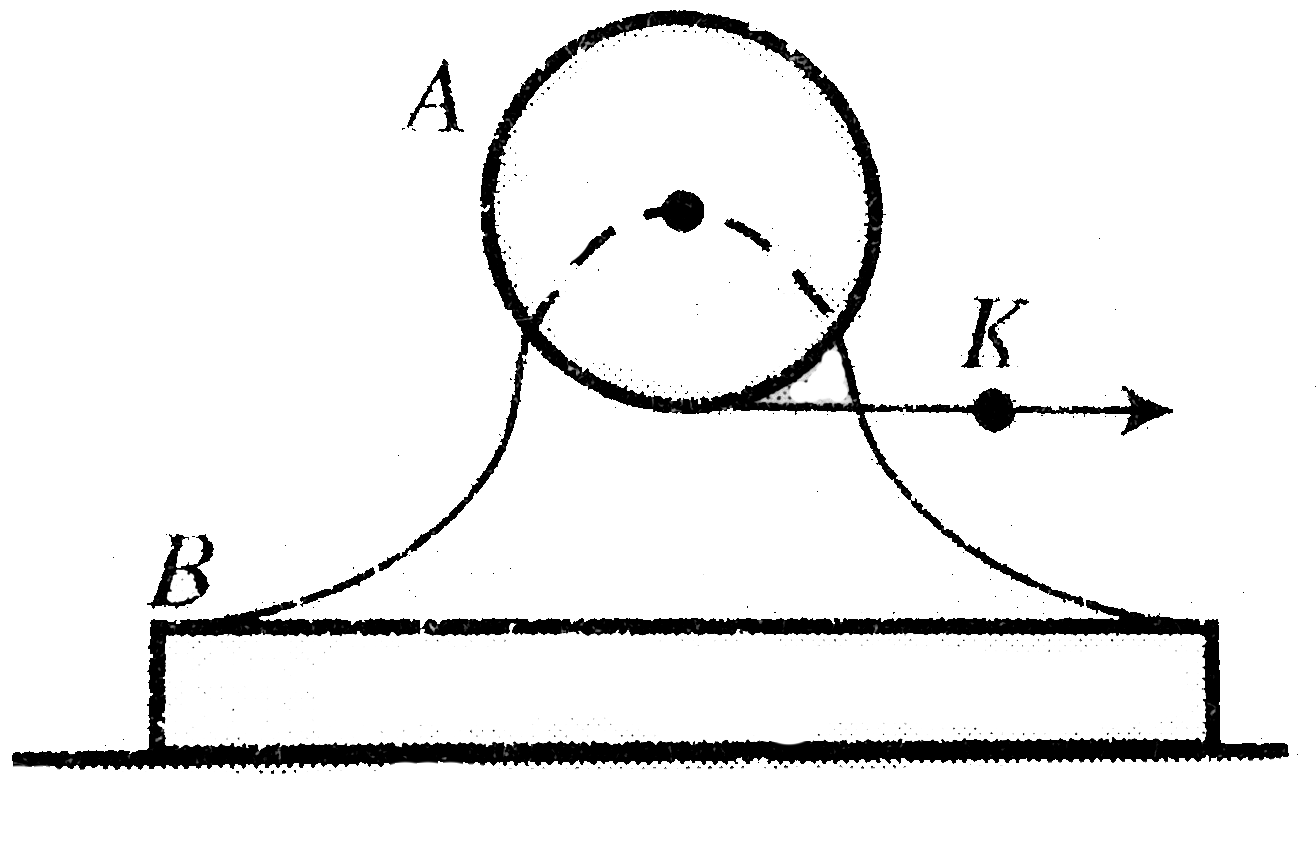
View SolutionIn the figure shown a plank of mass m is lying at rest on a smooth horizontal surface. A cylinder of same mass m and radius r is rotated to an angular speed w0 and then gently placed on the plank. It is found that by the time the slipping between the plank and the cylinder cease, 50% of total kinetic energy of the cylinder and plank system is lost. Assume that plank is long enough and um is the coefficient of friction between the cylinder and the plank.
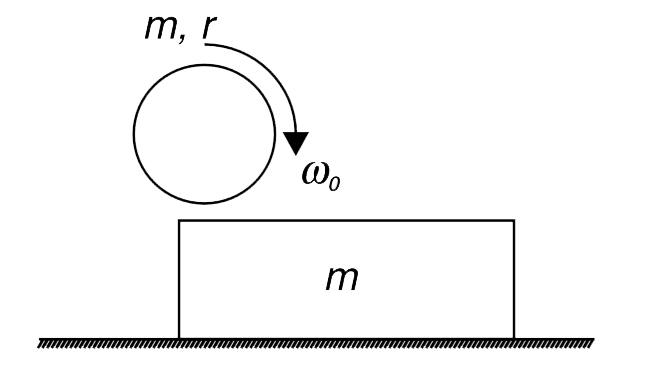
(a) Find the final velocity of the plank.
(b) Calculate the magnitude of the change in angular momentum of the cylinder about its centre of mass.
(c) Distance moved by the plank by the time slipping ceases between cylinder and plank.
View Solution

