A thin uniform rod of mass m moves translationally with acceleration a due to two antiparallel forces of lever arm l. One force is of magnitude F and acts at one extreme end. The length of the rod is
2(F+ma)lma
l(1+Fma)
(F+ma)l2ma
malma+F
The correct Answer is:A
Topper's Solved these Questions
- ROTATIONAL MOTIONBook:DC PANDEYChapter:ROTATIONAL MOTIONExercise:More than one option is correct
Explore 36 Videos
- ROTATIONAL MOTIONBook:DC PANDEYChapter:ROTATIONAL MOTIONExercise:Comprehension Type Questions
Explore 41 Videos
- ROTATIONAL MOTIONBook:DC PANDEYChapter:ROTATIONAL MOTIONExercise:Integer Type Questions
Explore 17 Videos
- ROTATIONAL MECHANICSBook:DC PANDEYChapter:ROTATIONAL MECHANICSExercise:Subjective Questions
Explore 2 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBook:DC PANDEYChapter:SEMICONDUCTORS AND ELECTRONIC DEVICESExercise:More than One Option is Correct
Explore 3 Videos
Similar Questions
A thin uniform rod of mass m=1kg moves translationally with acceleration a=2 ms−1 due to two antiparallel forces of arm-length l=20 cm . One forces is of magnitude 5 N and acts at one extreme end. Find the length of the rod.

View SolutionA thin uniform rod AB of mass m=1.0kg moves translationally with acceleration w=2.0m/s2 due to two antiparallel forces F1 and F2 (figure). The distance between the points at which these forces are applied is equal to a=20cm. Besides, it is known that F2=5.0N. Find the length of the rod.
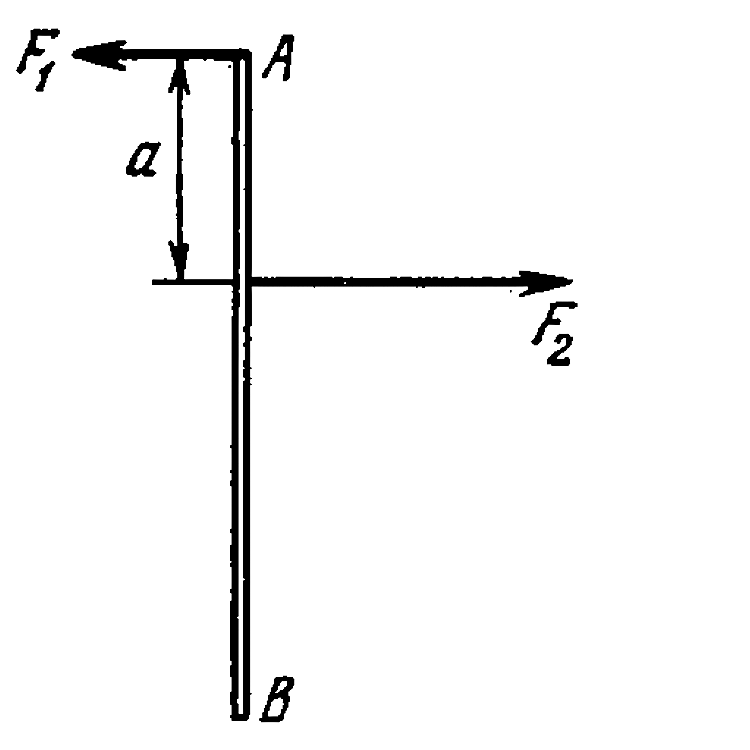
View Solution
Knowledge Check
A thin uniform rod of mass m moves translationally with acceleration a due to two antiparallel forces of level arm I. One force is of magnitude F and acts at one extreme end. The length of the rod is
Amalma+FB2(F+ma)lmaCl(l+Fma)D(F+ma)l2maA thin uniform rod AB of mass 1kg move translationally with acceleration a=2m/s2 due to two antiparallel force as shown. If l=20cm then:
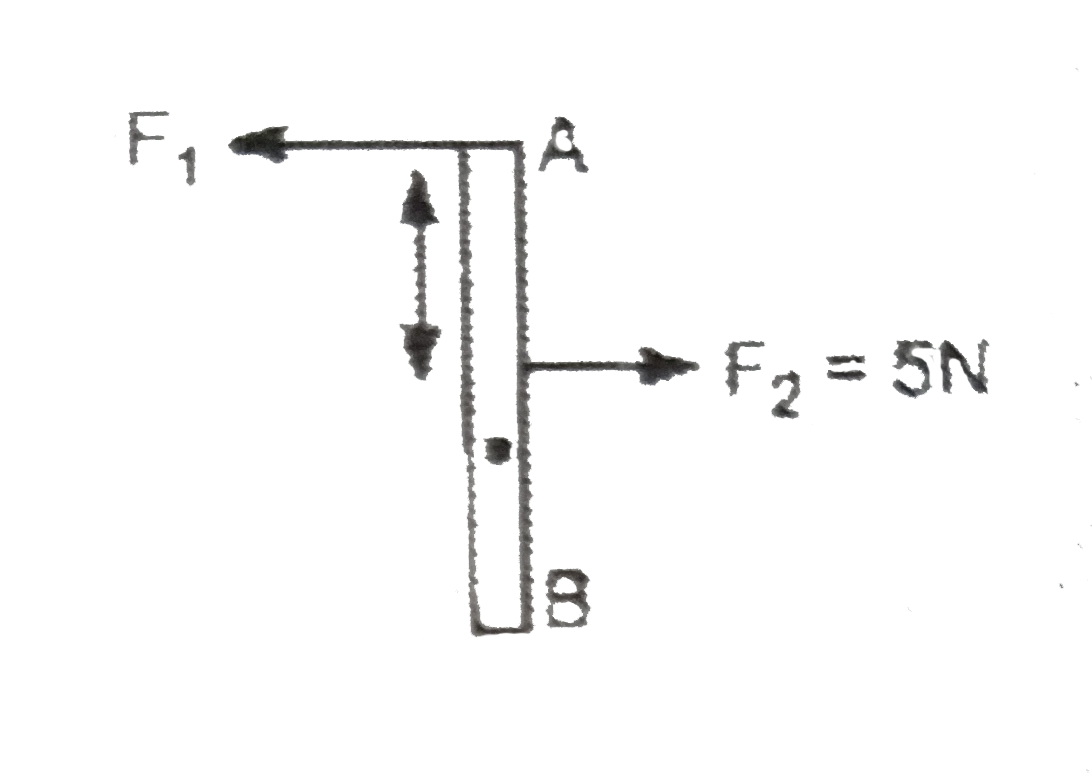 AF1=3NBF1=5NCLength of rod is 1mDLength of rod is 80cm
AF1=3NBF1=5NCLength of rod is 1mDLength of rod is 80cmA thin uniform rod AB of mass 1 kg moves translationally with acceleration a=2m/s2 due to two antiparallel forces F1 & F2. The distance between the points at which these forces are applied is equal to l=0.2m. If force F−(1)=8N then find the length of the rod in meter
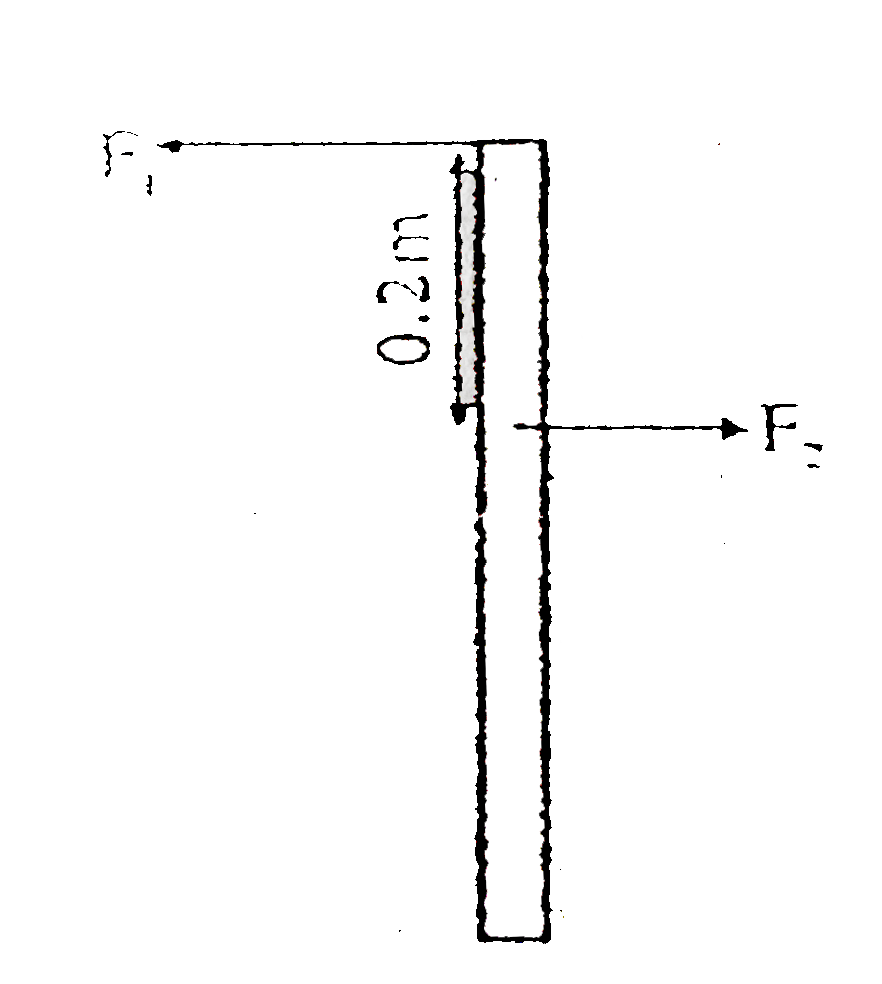 A1 mB2 mC3 mD4 m
A1 mB2 mC3 mD4 m
A thin uniform rod AB of mass 1 kg moves translationally with acceleration a=2m/s2 due to two antiparallel forces F1 & F2. The distance between the points at which these forces are applied is equal to l=0.2m. If force F−(1)=8N then find the length of the rod in meter
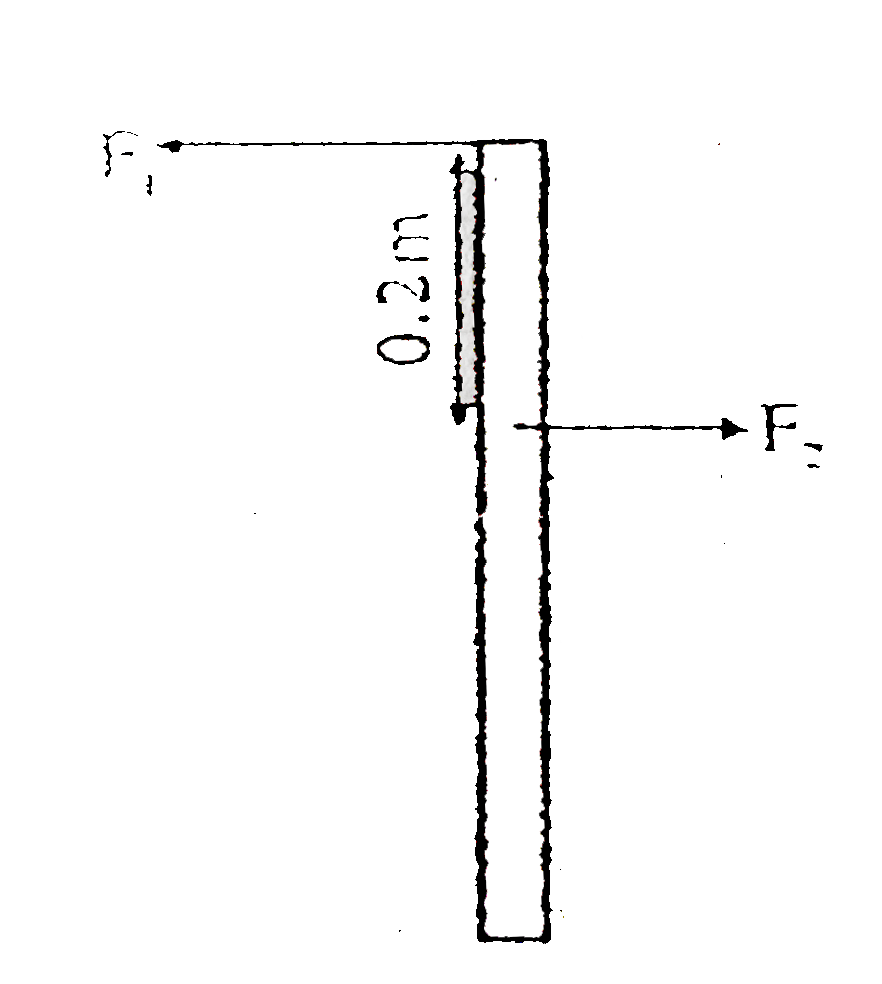
View SolutionA Thin uniform rod AB of mass m=1.0kg moves translationally with acceleration a=2.0m/s2 due to two antiparallel forces F1 and F2. The distance between the points at which these forces are applied is equal to d=20cm. Besides, it is known that F2=5.0N. Find the length of the rod.

View SolutionIn the given figure, thin uniform rod AB of mass kg moves translationally with acceleration a=2ms^(2)due→twoantiparal≤lforcesF_(1) ,F_(2).Thedistancebetweenthep∮satwhichtheseforcesareappliedisequal→0.2 m.IfforceF_(1)=8 N, then find the length of the rod in meter.
'(##CEN_KSR_PHY_JEE_C09_E01_022_Q11##)'
View Solution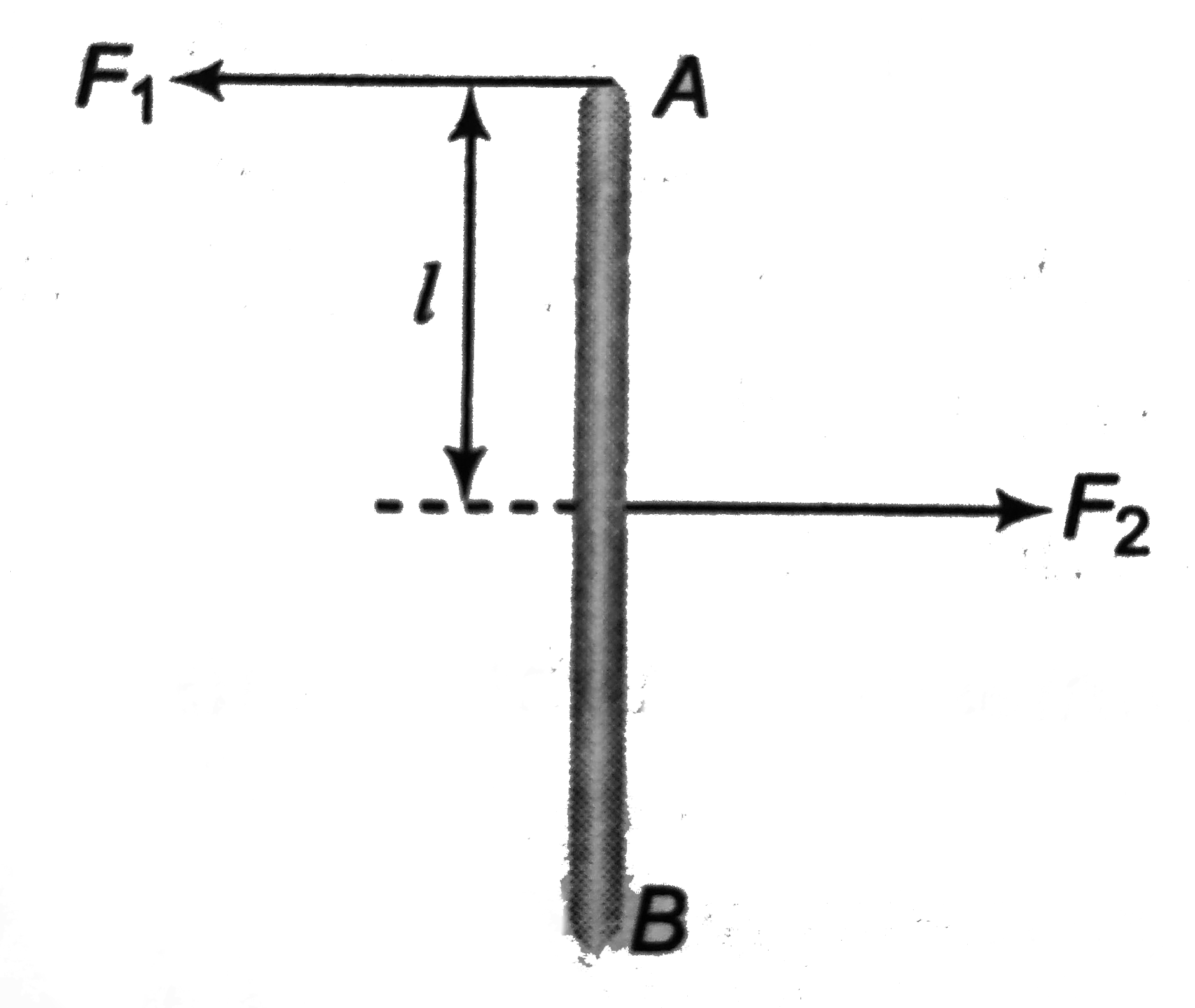
A thin uniform rod AB of mass m=1kg moves translationally with acceleration a=2m/s2 and to two anitiparallel forces F1 and F2. The distance between the points at which these forces are applied is equal to l=20cm besides it is known that F2=5N find the length of the rod.
View Solution
A thin uniform rod AB of mass m=1kg moves translationally with acceleration a=2m/s2 and to two anitiparallel forces F1 and F2. The distance between the points at which these forces are applied is equal to l=20cm besides it is known that F2=5N find the length of the rod.
View Solution

