The ends of thin threads tightly wound on the axle of radius r of the Maxwell disc are attached to a horizontal bar. When the disc unwinds, the bar is raised to keep the disc at the same height. The mass of the disc with the axle is equal to m, the moment of inertia of the arrangement relative to its axis is I. Find the tension of each thread and the acceleration of the bar.
For equilibrium of the disc and axle
or
As the disc unwinds, it has an angular acceleration given by
or
The corresponding linear acceleration is
Since the disc remains stationary under the combined action of this acceleration and the acceleration of the bar which is transmitted to the axle, we must have

Topper's Solved these Questions
- PHYSICAL FUNDAMENTALS OF MECHANICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:PHYSICAL FUNDAMENTALS OF MECHANICSExercise:Elastic Deformation Of Asolid Body
Explore 25 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:PHYSICAL FUNDAMENTALS OF MECHANICSExercise:Hydrodynamics
Explore 25 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:PHYSICAL FUNDAMENTALS OF MECHANICSExercise:Universal Gravitation
Explore 34 Videos
- OSCILLATIONS AND WAVESBook:IE IRODOV, LA SENA & SS KROTOVChapter:OSCILLATIONS AND WAVESExercise:Electromagnetic Waves, Radiation
Explore 36 Videos
- THERMODYNAMICS AND MOLECULAR PHYSICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:THERMODYNAMICS AND MOLECULAR PHYSICSExercise:Transport Phenomena
Explore 38 Videos
Similar Questions
A uniform disc of radius R has a round disc of radius R/3 cut as shown in Fig. The mass of the remaining (shaded) portion of the disc equals M. Find the moment of inertia of such a disc relative to the axis passing through geometrical centre of original disc and perpendicular to the plane of the disc.
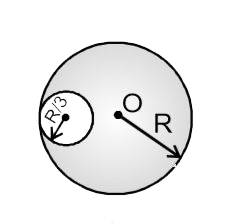
View SolutionMoment of inertia of a disc about an axis parallel to diameter and at a distance x from the centre of the disc is same as the moment of inertia of the disc about its centre axis. The radius of disc is R. The value of x is
View Solution
Knowledge Check
One quarter of the disc of mass m is removed. If r be the radius of the disc, the new moment of inertia is
A32mr2Bmr22C38mr2DNone of theseA ring and a disc have same mass and same radius. Then ratio of moment of inertia of ring to the moment of inertia of disc is
A4B2C0.5D1Moment of inertia of disc about the tangent parallel to plane is I. The moment of inertia of disc about tangent and perpendicular to its plane is
AMR2nBMR2n2tCMrωtDMrωt
A uniform disc of radius R=20cm has a round cut as shown in figure. The mass of the remaining (shaded) portion of the disc equals m=7.3kg. Find the moment of inertia of such a disc relative to the axis passing through its centre of inertia and perpendicular to the plane of the disc.

View SolutionA disc is of mass M and radius r. The moment of inertia of it about an axis tangential to its edge and in plane of the disc or parallel to its diameter is
View SolutionA circular disc is of mass M and radius r. From it a circualr piece is cut out with a radius of the disc as its diameter. Find the moment of inertia of the remainder about the axix of the disc
View SolutionThe moment of inertia of a uniform circular disc of radius R and mass M about an axis passing from the edge of the disc and normal to the disc is.
View SolutionA disc of mass M and radius R rolls on a horizontal surface and then rolls up an inclined plane as shown in the figure. If the velocity of the disc is v, the height to which the disc will rise will be:

View Solution

