A disc of mass M and radius R rolls on a horizontal surface and then rolls up an inclined plane as shown in the figure. If the velocity of the disc is v, the height to which the disc will rise will be:

3v22g
4v24g
v24g
v22g
12mv2+12Iω2=mgh
12mv2+12MR22v2R2=mgh
34mv2=mgh
h=3v24g

Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION BOOK - PHYSICS WALLAHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTION EXERCISE - LEVEL-2
30 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION BOOK - PHYSICS WALLAHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTION EXERCISE - NEET PAST 5 YEARS QUESTIONS
22 Videos
- SEMICONDUCTOR ELECTRONICS BOOK - PHYSICS WALLAHCHAPTER - SEMICONDUCTOR ELECTRONICS EXERCISE - NEET PAST 5 YEAR QUESTION
23 Videos
- THERMAL PROPERTIES OF MATTER BOOK - PHYSICS WALLAHCHAPTER - THERMAL PROPERTIES OF MATTER EXERCISE - NEET Past 5 Years Questions
12 Videos
Similar Questions
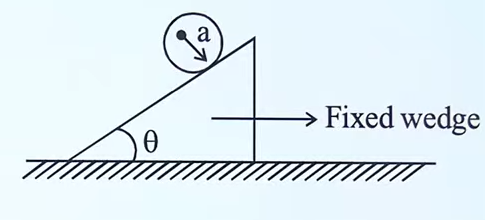
A disc having radius 'a' is rolling on an inclined plane as shown in figure. If acceleration of disc 2bgsin(θ) then find b
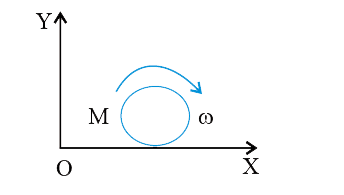
View SolutionA disc of mass M and radius R is rolling with angular speed w on horizontal plane as shown. The magnitude of angular momentum of the disc about the origin O is :
View Solution
Knowledge Check
A disc of mass M and radius R rolls on a horizontal surface and then rolls up an inclined plane as shown in the figure. If the velocity of the disc is v, the height to which the disc will rise will be:
 A3v22gB3v24gCv24gDv22g
A3v22gB3v24gCv24gDv22gA disc of mass M and radius R rolls on a horizontal surface and then rolls up an inclined plane as shown in the figure. If the velocity of the disc is v, the height to which the disc will rise will be:
 A3v22gB4v24gCv24gDv22g
A3v22gB4v24gCv24gDv22gA uniform disc of mass m and radius r rolls without slipping along a horizontal surface and ramp, as shown above. The disk has an initial velocity of υ . What is the maximum height h to which the center of mass of the disc rises ?
 Ah=υ22gBh=3υ24gCh=υ2gDh=3υ22g
Ah=υ22gBh=3υ24gCh=υ2gDh=3υ22g
A semicircle disc of mass M and radius R is held on a rough horizontal surface as shown in figure. The centre of mass C of the disc is at a distance of 4R3π from the point O. Now the disc is released from this position so that it starts rolling without slipping. Find
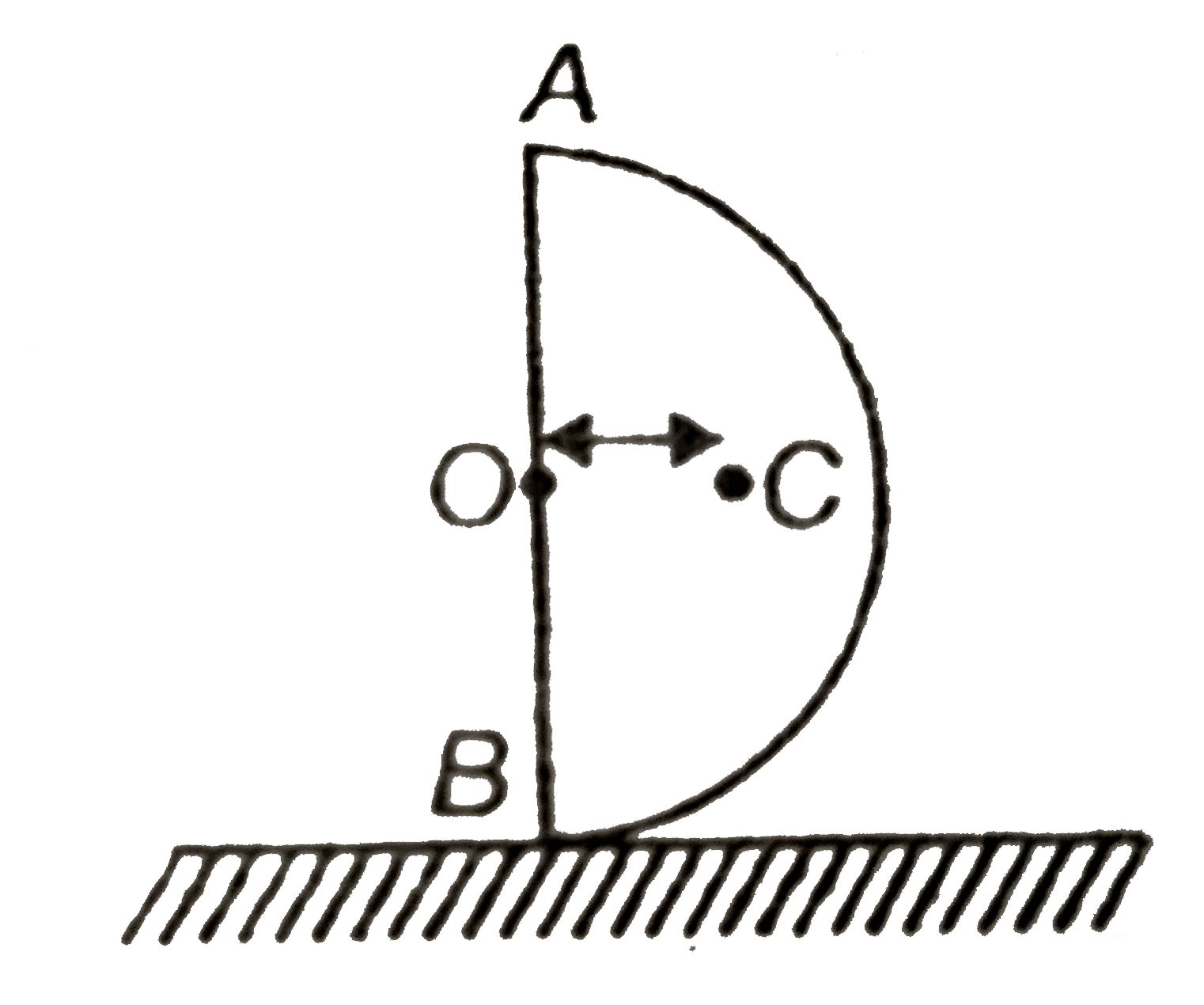
(a) The angular acceleration of the disc at the moment it is relased from the given position.
(b) The minimum co-efficient of fricition between the disc and ground so that it can roll without slipping.
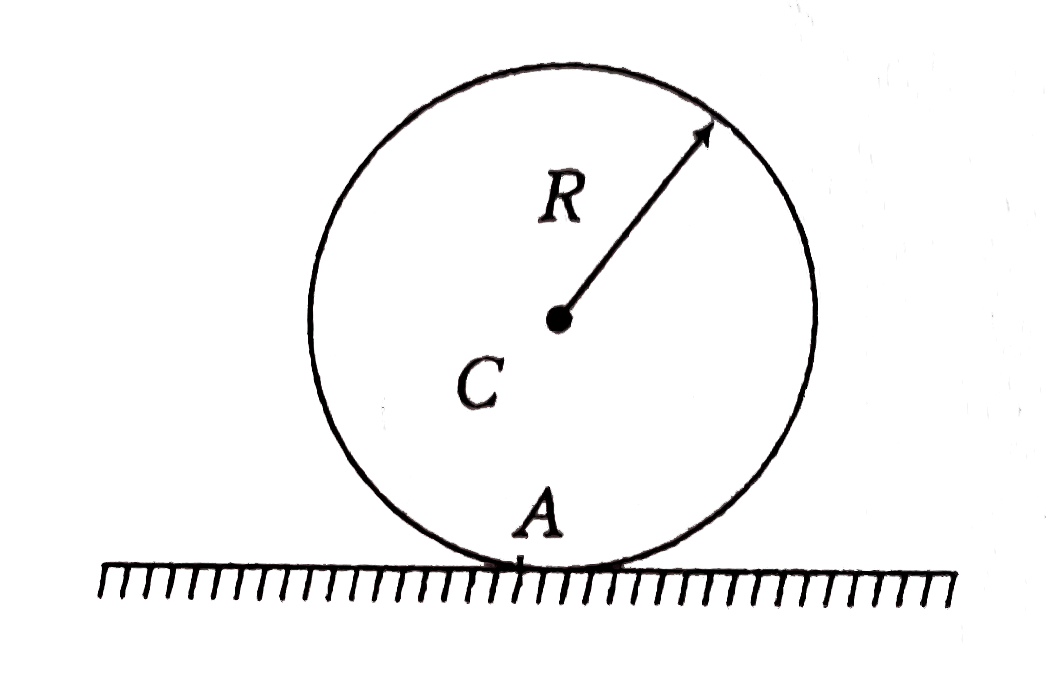
View SolutionA disc of radius R rolls on a rough horizontal surface. The distance covered by the point A in one revolution is
View SolutionA sphere a ring and a disc of same mass and radius are allowed to roll down three similar sufficiently rough inclined planes as shown in the figure from same height.
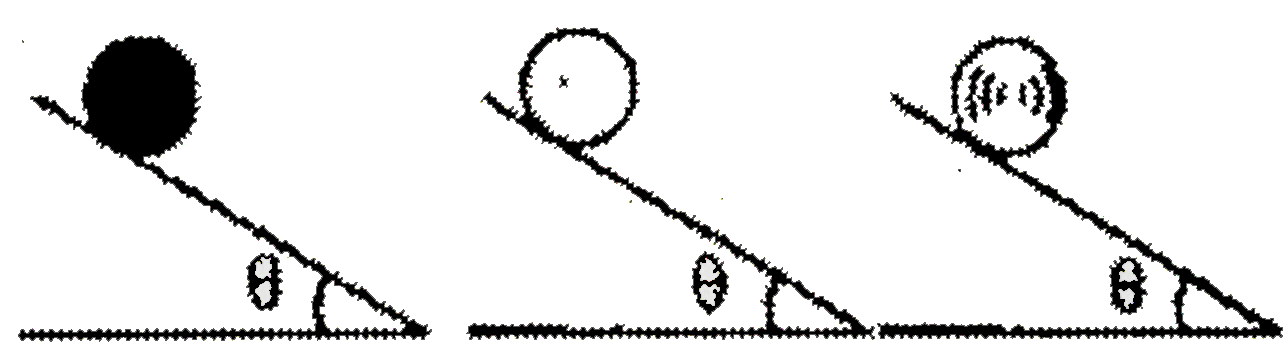
Which of the following order is true for final linear velocity of the bodies?
View SolutionA disc of mass 4.8 kg and radius 1 m is rolling on a horizontal surface without sliding with angular velocity of 600 rotations/min. What is the total kinetic energy of the disc ?
View SolutionA sphere a ring and a disc of same mass and radius are allowed to roll down three similar sufficiently rough inclined planes as shown in the figure from same height.
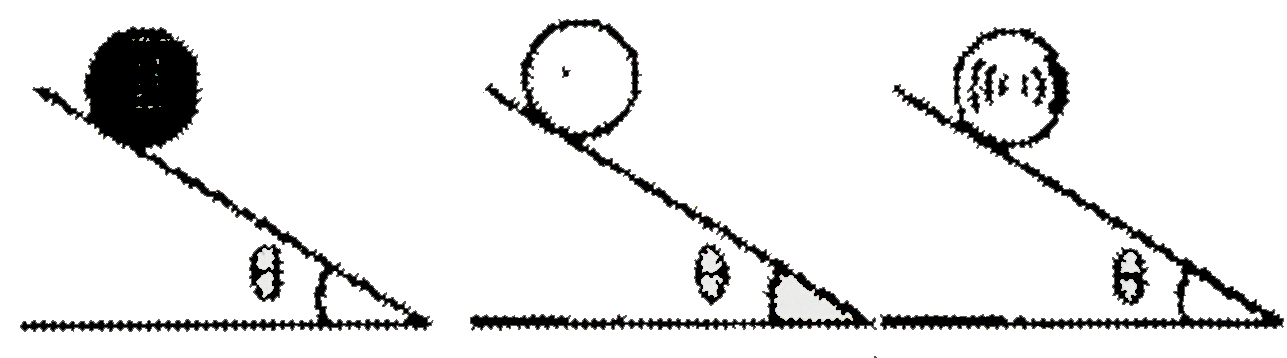
Which of the follwing order is true for final KE of the bodies?
View Solution
