A cannon of mass M starts sliding freely down a smooth inclined plane at an angle α to the horizontal. After the cannon covered the distance l, a shot was fired, the shell leaving the cannon in the horizontal direction with a momentum p. As a consequence, the cannon stopped. Assuming the mass of the shell to be negligible, as compared to that of cannon, determine the duration of the shot.
Velocity of cannon as well as that of shell equals √2glsinα down the inclined plane taken as the positive x-axis. From the linear impulse momentum theorem in projection form along x-axis for the system (cannon+shell) i.e. Δpx=FxΔt:
pcosα−M√2glsinα=MgsinαΔt (as mass of the shell is negligible)
or, Δt=pcosα−M√2glsinαMgsinα
Topper's Solved these Questions
- PHYSICAL FUNDAMENTALS OF MECHANICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:PHYSICAL FUNDAMENTALS OF MECHANICSExercise:Universal Gravitation
Explore 34 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:PHYSICAL FUNDAMENTALS OF MECHANICSExercise:Dynamics Of A Solid Body
Explore 56 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:PHYSICAL FUNDAMENTALS OF MECHANICSExercise:The Fundamental Equation Of Dynamics
Explore 59 Videos
- OSCILLATIONS AND WAVESBook:IE IRODOV, LA SENA & SS KROTOVChapter:OSCILLATIONS AND WAVESExercise:Electromagnetic Waves, Radiation
Explore 36 Videos
- THERMODYNAMICS AND MOLECULAR PHYSICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:THERMODYNAMICS AND MOLECULAR PHYSICSExercise:Transport Phenomena
Explore 38 Videos
Similar Questions
A mass m slides down a fixed plane inclined at an angle a to the horizontal plane after covering the entire length of the inclined plane. The height of the inclined plane is h and the coefficient of friction over both surfaces is μ.
View SolutionA cannot fires from under a shelter inclined at an angle α to the horizontal (Fig.). The cannot is at point A at a (distance l from the base of the shelter (point B). The initial velocity of the shell is v0, and its trajectory lies in the plane of the figure. Determine the maximum range Lmax of the shell.

View Solution
Knowledge Check
A trolley containing a liquid slides down a smooth inclined plane of angle α with the horizontal. Find the angle of inclination θ of the free surface with the horizontal.
 Aθ=α2Bθ=2αCθ=zeroDθ=α
Aθ=α2Bθ=2αCθ=zeroDθ=αA trolley containing a liquid slides down a smooth inclined plane of angle α with the horizontal. Find the angle of inclination θ of the free surface with the horizontal.
 AEqual to αBGreater than αCEqual to α2DLesser than α
AEqual to αBGreater than αCEqual to α2DLesser than αImagine a cannon being fired on the surface of the moon. Then
Athe sound will be heard at the surface of the earth during all seasonsBthe sound will not be heard at the surface of the earth but will be heard on the moon.Cthe sound will be heard at the surface of the earth during the rainy seasonDno sound will be heard on the earth or on the moon
A cannon of mass m1 fires a shell of mass m2 with speed v0 relative to the barrel which is inclined at an angle α with horizontal . Find the recoil speed of cannon if it is placed on ice.
View SolutionConsider an object P on an inclined plane of inclination β.
A shot is fired O at an angle α with horizontal. Find the relation between α and β, if the shot hits the object horizontally.

View SolutionA smooth inclined plane is inclined at an angle θ with the horizontal. A body starts from rest and slides down the inclined surface. The time taken by the body to reach the bottom is
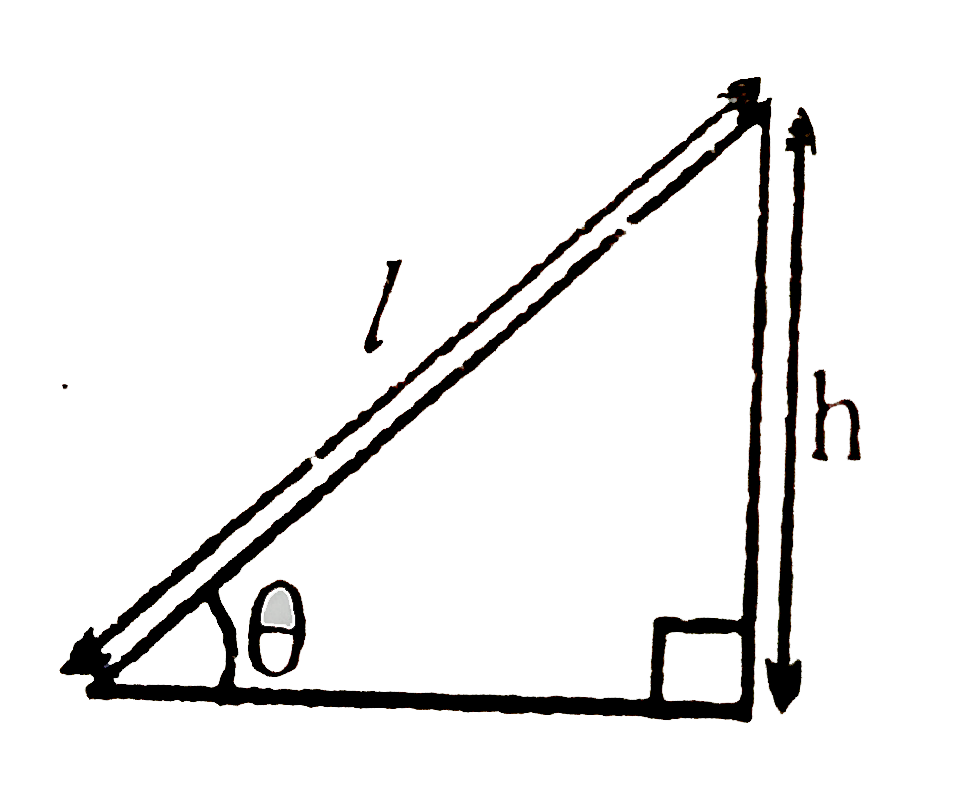
View SolutionA small mass slides down an inclined plane of inclination θ the horizontal the coefficient of friction is m=μ0x, where x is the distance by the mass before it stops is .
View SolutionA cannon of mass 5m (including a shell of mass m) is at rest on a smooth horizontal ground, fires the shell with its barrel at an angle θ with the horizontal at a velocity u relative to cannon. Find the horizontal distance of the point where shell strikes the ground from the initial position of the cannon :-
View Solution

