A horizontally flying bullet of mass m gets stuck in a body of mass M suspended by two identical threads of length l (figure).
As a result, the threads swerve through an angle θ. Assuming m<<M, find:
(a) the velocity of the bullet before striking the body,
(b) the fraction of the bullet's initial kinetic energy that turned into heat.
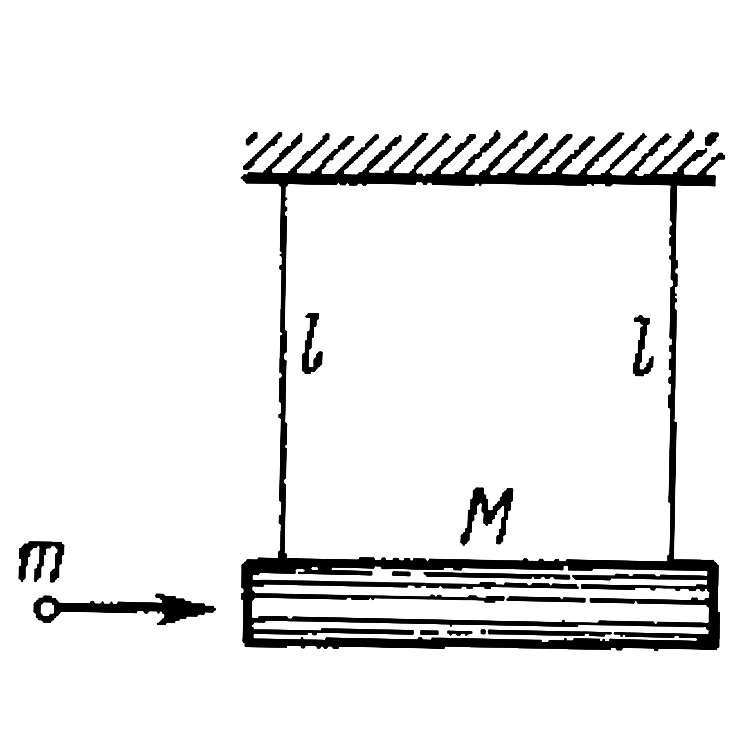
From conservation of momentum, for the system (bullet+body) along the initial direction of bullet
mv0=(m+M)v, or, v=mv0m+M
Topper's Solved these Questions
- PHYSICAL FUNDAMENTALS OF MECHANICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:PHYSICAL FUNDAMENTALS OF MECHANICSExercise:Universal Gravitation
Explore 34 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:PHYSICAL FUNDAMENTALS OF MECHANICSExercise:Dynamics Of A Solid Body
Explore 56 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:PHYSICAL FUNDAMENTALS OF MECHANICSExercise:The Fundamental Equation Of Dynamics
Explore 59 Videos
- OSCILLATIONS AND WAVESBook:IE IRODOV, LA SENA & SS KROTOVChapter:OSCILLATIONS AND WAVESExercise:Electromagnetic Waves, Radiation
Explore 36 Videos
- THERMODYNAMICS AND MOLECULAR PHYSICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:THERMODYNAMICS AND MOLECULAR PHYSICSExercise:Transport Phenomena
Explore 38 Videos
Similar Questions
A vertically oriented uniform rod of mass M and length l can rotate about its upper end. A horizontally flying bullet of mass m strikes the lower end of the rod and gets stuck in it, as a result, the rod swings through an angle α. Assuming that m<<M, find:
(a) the velocity of the flying bullet,
(b) the momentum increment in the system "bullet-rod" during the impact, what causes the change of that momentum,
(c) at what distance x from the upper end of the rod the bullet must strike for the momentum of the system "bullet-rod" to remain constant during the impact.
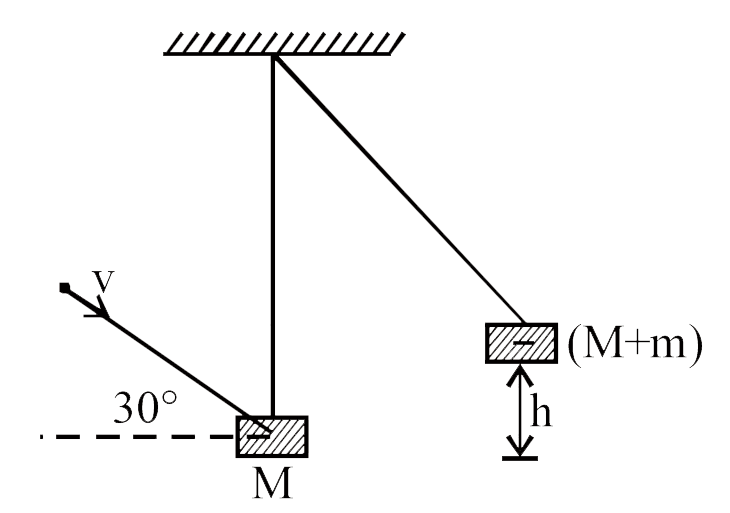
View SolutionA bullet of mass 20 g hits a block of mass 1.98 kg suspended from a massless string of length 100 cm and sticks to it. The bullet flies down at an angle of 30º to the horizontal with a velocity of 200 m/s. Through what height the block will rise-
View Solution
Knowledge Check
A body of mass m strikes another body at rest of mass mg. Assuming the impact to be inelastic the fraction of the initial kinetic energy transformed into heat during the contact is
A0.1B0.2C0.5D0.64Two small balls of mass m each are suspended side by side by two equal threds to length L. If the distance between the upper ends of the threads be a, the angle θ that the threads will make with the vertical due to attraction between the balls is :
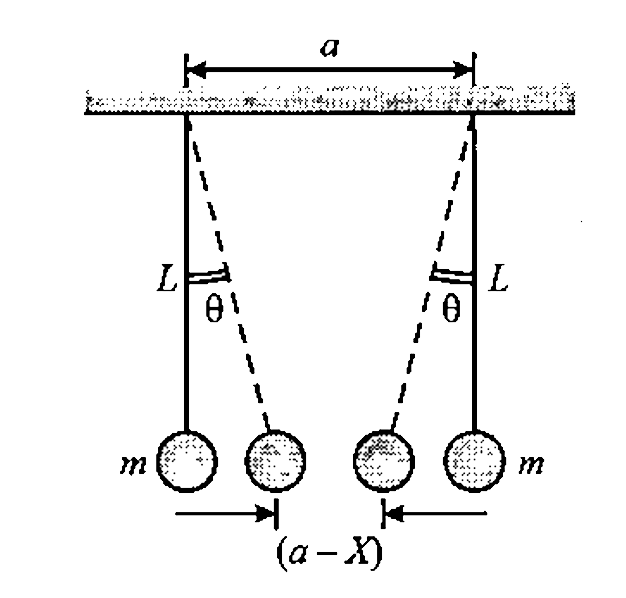 Atan−1(a−X)gmGBtan−1mG(a−X)2gCtan−1(a−X)2gmGDtan−1(a2−X2)gmG
Atan−1(a−X)gmGBtan−1mG(a−X)2gCtan−1(a−X)2gmGDtan−1(a2−X2)gmGA bullet of mass m=50 gm strikes (Δt≈0)a sand bag of mass M =5 kg hanging from a fixed point, with a horizontal velocity →vp. If bullet sticks to the sand bag then the ratio of final & initial kinetic energy of the bullet is
A10−2B10−3C10−6D10−4
Two idential pith balls , each of mass m and charge +q. are suspended from a point with threads of length l each. If in equiilbrium state θ be the angle which each thread makes with vertical in equilibrium , find value of charge on each ball.
View SolutionA bullet of mass M is fired with a velocity 50m/s at an angle with the horizontal. At the highest point of its trajectory, it collides head-on with a bob of mass 3M suspended by a massless string of length 10/3 metres and gets embeded in the bob. After the collision, the string moves through an angle of 120∘. Find
(i) the angle θ,
(ii) the vertical and horizontal coordinates of the initial position of the bob with respect to the point of firing of the bullet. Take g=10m/s2
View SolutionTwo identical spheres of mass m and charge q are suspended from a common point by two threads of the same length l and it is found that threads make an angle θ with the vertical when the spheres are in equilibrium . Calculate the value of q.
View SolutionA bullet of mass 5 g travels with a speed of 500m/s. If it penetrates a fixed target which offers a constant resistive force of 1000N to the motion of the bullet, find (a) the initial kinetic energy of the bullet (b) the distance through which the bullet has penetrated.
View SolutionTwo identical tennis balls each having mass 'm' and charge 'q' are suspended from a fixed point by threads of length 'l'. What is the equilibrium separation when each thread makes a small angle 'θ' with the vertical ?
View Solution

